Argumento de um número complexo
Referência : Ramos, F., (2014) Argumento de um número complexo, Rev. Ciência Elem., V2(4):079
Autores: Filipe Ramos
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2014.079]

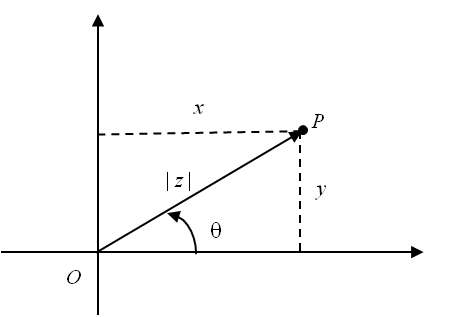
Argumento de um número complexo não nulo, \(z = x + i y\), com \(x, \, y\) números reais não simultaneamente nulos, é qualquer número real \(\theta\) tal que \(\displaystyle \cos\,\theta=\frac{x}{|z|}\) e \(\displaystyle \sin\,\theta=\frac{y}{|z|}\), onde \(|z|=\sqrt{x^{2}+y^{2}}\) é o módulo do número complexo \(z\).
Escreve-se habitualmente \(\theta=\arg\left(z\right)\).
Geometricamente:
Onde \(\theta\) é a amplitude do ângulo, medida em radianos, de vértice na origem, \(O\), cujo lado origem é o semi-eixo real positivo e o lado extremidade é a semi-reta \(\dot{O}P\) em que \(P\) é o afixo de z.
Nota
Decorre da definição anterior que para cada número complexo \(z\) não existe um argumento univocamente determinado pois, se \(\theta=\arg\left(z\right)\), também, \(\theta+2k\pi = \arg\left(z\right)\) para qualquer número inteiro \(k\).
O número complexo \(z = 0 \) tem argumento indeterminado, pois qualquer número real \(\theta\) pode ser um argumento para \(z = 0\).
Exemplo
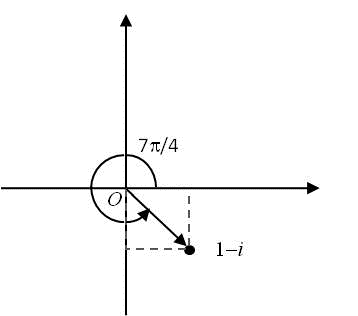
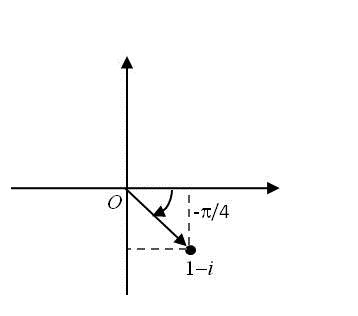
O complexo \(z=1-i\), tem por exemplo, os argumentos \(\displaystyle \theta_{1}=\frac{7\pi}{4}\),\(\displaystyle \theta_{2}=-\frac{\pi}{4}\), \(\displaystyle \theta_{3}=\frac{15\pi}{4}\), ou genericamente \(\displaystyle \theta =\frac{7\pi}{4} + 2k \pi\), onde \(k\) é qualquer número inteiro.
Geometricamente:
Ver
- Argumento positivo mínimo de um número complexo
- Argumento principal de um número complexo
- Representação polar (ou trigonométrica) de um número complexo
Referências
1. Carreira,A. Nápoles,S.(1998) -Variável Complexa: Teoria Elementar e Exercícios Resolvidos.McGraw-Hill, ISBN:972-8298-69-2.
2. Marsden,J.E., Hoffman,J.M. (1998) - Basic Complex Analysis,3ª edição,.W.H. Freeman and Company. ISBN-10: 0-7167-2877-X.
3. Silva,J.S. (1975) - Compêndio de Matemática, 1º Volume (2º TOMO), Gabinete de Estudos e Planeamento do Ministério da Educação e Cultura.
Criada em 03 de Fevereiro de 2012
Revista em 11 de Junho de 2012
Aceite pelo editor em 11 de Junho de 2012