Diferenças entre edições de "Resolução de triângulos"
(→Relações entre os seus elementos) |
|||
| (62 edições intermédias de um utilizador não apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | <span style="font-size:8pt"><b>Referência : </b> | + | <span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) ''Resolução de triângulos'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(3):079 |
<br> | <br> | ||
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | <span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | ||
| − | <span style="font-size:8pt"><b>Editor</b>: <i> | + | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Jfgomes47|José Ferreira Gomes]]</i></span><br> |
| + | <span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.079 https://doi.org/10.24927/rce2017.079]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-079.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
---- | ---- | ||
| − | + | __TOC__ | |
==O que é resolver um triângulo== | ==O que é resolver um triângulo== | ||
Em qualquer [[Triângulo|triângulo]] podemos considerar como ''elementos principais'' os seus três lados e os três ângulos internos e todos os outros elementos como ''elementos secundários'', como por exemplo, as alturas, as medianas, o raio do círculo circunscrito, etc. | Em qualquer [[Triângulo|triângulo]] podemos considerar como ''elementos principais'' os seus três lados e os três ângulos internos e todos os outros elementos como ''elementos secundários'', como por exemplo, as alturas, as medianas, o raio do círculo circunscrito, etc. | ||
| − | A '''resolução de triângulos''' consiste em determinar alguns elementos do triângulo a partir de elementos já conhecidos. Quando | + | A '''resolução de triângulos''' consiste em determinar alguns elementos do triângulo a partir de elementos já conhecidos. Quando se diz determinar os elementos entenda-se determinar a medida desses elementos. |
==Resolução de triângulos retângulos== | ==Resolução de triângulos retângulos== | ||
| Linha 32: | Linha 35: | ||
Pelas definições de [[Seno de um ângulo agudo|seno]] e [[Cosseno de um ângulo agudo|cosseno]] de um ângulo agudo sabemos que \(\displaystyle \sin B= \frac{b}{a}\) e \(\displaystyle \cos B= \frac{c}{a}\) donde resulta que, \(b=a \, \sin B \,\) e \(c= a \, \cos B\). | Pelas definições de [[Seno de um ângulo agudo|seno]] e [[Cosseno de um ângulo agudo|cosseno]] de um ângulo agudo sabemos que \(\displaystyle \sin B= \frac{b}{a}\) e \(\displaystyle \cos B= \frac{c}{a}\) donde resulta que, \(b=a \, \sin B \,\) e \(c= a \, \cos B\). | ||
| − | |||
Como \(B\) e \(C\) são ângulos complementares temos ainda que \(\sin B= \cos C\) e que \(\cos B= \sin C\), passando as fórmulas anteriores a serem equivalentes a \(b=a \, \cos C\) e \(c= a \, \sin C\), respetivamente. | Como \(B\) e \(C\) são ângulos complementares temos ainda que \(\sin B= \cos C\) e que \(\cos B= \sin C\), passando as fórmulas anteriores a serem equivalentes a \(b=a \, \cos C\) e \(c= a \, \sin C\), respetivamente. | ||
| Linha 38: | Linha 40: | ||
===Resolução de triângulos retângulos=== | ===Resolução de triângulos retângulos=== | ||
| − | Sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Como estamos a considerar triângulos retângulos um dos ângulos já é conhecido, o ângulo reto, por isso bastam mais dois elementos. | + | Sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Como estamos a considerar triângulos retângulos um dos ângulos já é conhecido, o ângulo reto, por isso bastam mais dois elementos. Existem assim <u>quatro casos</u> possíveis. |
| Linha 44: | Linha 46: | ||
Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, usamos as fórmulas \(b=a \, \sin B\) e \(c=a \, \cos B\) para determinar o comprimento dos dois catetos. | Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, usamos as fórmulas \(b=a \, \sin B\) e \(c=a \, \cos B\) para determinar o comprimento dos dois catetos. | ||
| − | + | {| border="0" cellspacing="0" | |
| − | + | |- | |
| − | <u>Exemplo</u>: | + | | <u>Exemplo</u>: |
Sabendo que a hipotenusa \(a=32,63 \mbox{ cm}\) e que o ângulo agudo \(B=34º\,52' \,8' '\), temos então que: | Sabendo que a hipotenusa \(a=32,63 \mbox{ cm}\) e que o ângulo agudo \(B=34º\,52' \,8' '\), temos então que: | ||
| Linha 57: | Linha 59: | ||
\(c=a \, \cos B \, \Leftrightarrow \, c=32,63 \times \cos (55º\,7' \,52' ') \, \Leftrightarrow \, c \simeq 18,65 \mbox{ cm}\) | \(c=a \, \cos B \, \Leftrightarrow \, c=32,63 \times \cos (55º\,7' \,52' ') \, \Leftrightarrow \, c \simeq 18,65 \mbox{ cm}\) | ||
| − | + | || | |
| − | + | [[Imagem:Resolex1-1.png|thumb|right|180px|Exemplo 1]] | |
| + | |} | ||
<span style="color:green">'''''2ºcaso'''''</span> - '''''São conhecidos um cateto e um ângulo agudo''''' | <span style="color:green">'''''2ºcaso'''''</span> - '''''São conhecidos um cateto e um ângulo agudo''''' | ||
Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, considerando o ângulo oposto ao cateto conhecido, sabemos que o seno desse ângulo é igual ao quociente entre o cateto conhecido (cateto oposto) e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o seno desse ângulo. Ou, se considerarmos o ângulo agudo cujo cateto adjacente é o cateto conhecido, sabemos que o cosseno desse ângulo é igual ao quociente entre o cateto conhecido e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o cosseno desse ângulo. Para determinar o terceiro lado do triângulo usamos o Teorema de Pitágoras. | Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, considerando o ângulo oposto ao cateto conhecido, sabemos que o seno desse ângulo é igual ao quociente entre o cateto conhecido (cateto oposto) e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o seno desse ângulo. Ou, se considerarmos o ângulo agudo cujo cateto adjacente é o cateto conhecido, sabemos que o cosseno desse ângulo é igual ao quociente entre o cateto conhecido e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o cosseno desse ângulo. Para determinar o terceiro lado do triângulo usamos o Teorema de Pitágoras. | ||
| − | + | {| border="0" cellspacing="0" | |
| − | + | |- | |
| − | <u>Exemplo</u>: | + | |<u>Exemplo</u>: |
Conhecidos o cateto \(c=57,4 \mbox{ cm}\) e o ângulo agudo \(C=46º\, 25'\) temos então que: | Conhecidos o cateto \(c=57,4 \mbox{ cm}\) e o ângulo agudo \(C=46º\, 25'\) temos então que: | ||
| Linha 76: | Linha 79: | ||
\(a^2=b^2+c^2 \, \Leftrightarrow \, (79,24)^2=b^2+(57,4)^2 \, \Leftrightarrow \, b \simeq 54,63 \mbox{ cm}\) | \(a^2=b^2+c^2 \, \Leftrightarrow \, (79,24)^2=b^2+(57,4)^2 \, \Leftrightarrow \, b \simeq 54,63 \mbox{ cm}\) | ||
| − | + | || | |
| + | [[Imagem:Resolex2-1.png|thumb|right|180px|Exemplo 2]] | ||
| + | |} | ||
<span style="color:green">'''''3ºcaso'''''</span> - '''''São conhecidos a hipotenusa e um cateto''''' | <span style="color:green">'''''3ºcaso'''''</span> - '''''São conhecidos a hipotenusa e um cateto''''' | ||
Para determinarmos o comprimento do terceiro lado do triângulo usamos diretamente o Teorema de Pitágoras. Conhecidos os três lados do triângulo, utilizamos as [[Relações trigonométricas num triângulo retângulo|razões trigonométricas]] para determinar a amplitude de cada um dos ângulos agudos. | Para determinarmos o comprimento do terceiro lado do triângulo usamos diretamente o Teorema de Pitágoras. Conhecidos os três lados do triângulo, utilizamos as [[Relações trigonométricas num triângulo retângulo|razões trigonométricas]] para determinar a amplitude de cada um dos ângulos agudos. | ||
| − | + | {| border="0" cellspacing="0" | |
| − | + | |- | |
| − | <u>Exemplo</u>: | + | |<u>Exemplo</u>: |
Conhecidos a hipotenusa \(a=18 \mbox{ cm}\) e o cateto \(b=9 \mbox{ cm}\) temos então que: | Conhecidos a hipotenusa \(a=18 \mbox{ cm}\) e o cateto \(b=9 \mbox{ cm}\) temos então que: | ||
| Linha 94: | Linha 99: | ||
\(C=90º-B \, \Leftrightarrow \, C=90º-30º=60º\) | \(C=90º-B \, \Leftrightarrow \, C=90º-30º=60º\) | ||
| − | + | || | |
| − | + | [[Imagem:Resolex3-1.png|thumb|right|140px|Exemplo 3]] | |
| + | |} | ||
<span style="color:green">'''''4ºcaso'''''</span> - '''''São conhecidos os dois catetos''''' | <span style="color:green">'''''4ºcaso'''''</span> - '''''São conhecidos os dois catetos''''' | ||
O comprimento da hipotenusa pode ser determinado através do Teorema de Pitágoras. Para se determinar a amplitude de cada um dos ângulos agudos usamos uma das [[Relações trigonométricas num triângulo retângulo|razões trigonométricas]]. | O comprimento da hipotenusa pode ser determinado através do Teorema de Pitágoras. Para se determinar a amplitude de cada um dos ângulos agudos usamos uma das [[Relações trigonométricas num triângulo retângulo|razões trigonométricas]]. | ||
| − | + | {| border="0" cellspacing="0" | |
| − | + | |- | |
| − | <u>Exemplo</u>: | + | |<u>Exemplo</u>: |
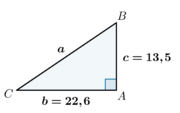
Conhecidos o cateto \(b=22,6 \mbox{ cm}\) e o cateto \(c=13,5 \mbox{ cm}\) temos então que: | Conhecidos o cateto \(b=22,6 \mbox{ cm}\) e o cateto \(c=13,5 \mbox{ cm}\) temos então que: | ||
| Linha 112: | Linha 118: | ||
\(C=90º-B \, \Leftrightarrow \, C=90º-(59º \, 8'\, 54' ')=30º \, 51'\, 6' '\) | \(C=90º-B \, \Leftrightarrow \, C=90º-(59º \, 8'\, 54' ')=30º \, 51'\, 6' '\) | ||
| + | || | ||
| + | [[Imagem:Resolex4.png|thumb|right|180px|Exemplo 4]] | ||
| + | |} | ||
| + | |||
==Resolução de triângulos quaisquer== | ==Resolução de triângulos quaisquer== | ||
| + | ===Relações entre os seus elementos=== | ||
| + | |||
| + | [[Imagem:Resoltriangobli.png|thumb|upright|200px|'''Figura 2''' - Triângulo obliquângulo]] | ||
| + | Considerando um triângulo obliquângulo (sem nenhum ângulo reto) \([ABC]\) e designemos por \(a\), \(b\) e \(c\) os lados desse triângulo e por \(A\), \(B\) e \(C\) os seus ângulos internos opostos a cada um dos lados, respetivamente (Fig.2). | ||
| + | |||
| + | Os seis elementos deste triângulo satisfazem relações importantes, tais como: | ||
| + | |||
| + | {| class="wikitable" align="center" | ||
| + | |- | ||
| + | | \(A+B+C=180º \quad \) || (soma das amplitudes dos ângulos internos de um triângulo) | ||
| + | |} | ||
| + | {| class="wikitable" align="center" | ||
| + | |- | ||
| + | | \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} \quad \] || ([[Lei dos senos]]) | ||
| + | |} | ||
| + | {| class="wikitable" align="center" | ||
| + | |- | ||
| + | | \(a^2=b^2+c^2-2bc \, \cos A \quad \) ou \(b^2=a^2+c^2-2ac \, \cos B \quad \) ou \(c^2=a^2+b^2-2ab\, \cos C \quad \)|| ([[Lei dos cossenos]]) | ||
| + | |} | ||
| + | |||
| + | |||
| + | ===Resolução de triângulos obliquângulos=== | ||
| + | |||
| + | As relações estabelecidas anteriormente permitem resolver um triângulo obliquângulo conhecidos alguns dos seus elementos. Já sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Assim podemos considerar <u>quatro casos</u>. | ||
| + | |||
| + | |||
| + | <span style="color:green">'''''1ºcaso'''''</span> - '''''São conhecidos dois ângulos e um lado''''' | ||
| + | |||
| + | Neste caso, para determinar a amplitude do ângulo desconhecido usa-se o facto da soma das amplitudes dos ângulos internos de um triângulo ser \(180º\). Assim, considerando \(A\) o ângulo desconhecido temos que \(A=180º-(B+C)\). Para determinarmos os lados \(b\) e \(c\), considerando \(a\) conhecido, usamos a [[Lei dos senos| lei dos senos]]. Aplicando esta lei temos então que: | ||
| + | |||
| + | \(\displaystyle \frac{b}{\sin B}=\frac{a}{\sin A} \, \Leftrightarrow \, b=\frac{a \, \sin B}{\sin A}\) e \(\displaystyle \frac{c}{\sin C}=\frac{a}{\sin A} \, \Leftrightarrow \, c=\frac{a \, \sin C}{\sin A}\). | ||
| + | |||
| + | {| border="0" cellspacing="0" | ||
| + | |- | ||
| + | | <u>Exemplo</u>: | ||
| + | |||
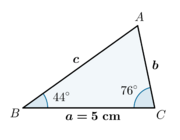
| + | Sabendo que \(B=44º\), \(C=76º\) e que \(a=5 \mbox{ cm}\) temos então que: | ||
| + | |||
| + | Cálculo de \(A\): \(\quad \quad A=180º-(B+C)=180º-(44º+76º)=60º\). | ||
| + | |||
| + | Cálculo de \(b\) e \(c\): \(\quad \quad \displaystyle b=\frac{a\, \sin B}{\sin A}=\frac{5 \times \sin 44º}{\sin 60º} \simeq 4,01 \mbox{ cm} \quad \quad\) e | ||
| + | \(\quad \quad \displaystyle c=\frac{a\, \sin C}{\sin A}=\frac{5 \times \sin 76º}{\sin 60º} \simeq 5,6 \mbox{ cm} \) | ||
| + | || | ||
| + | [[Imagem:Resolex5.png|thumb|right|180px|Exemplo 5]] | ||
| + | |} | ||
| + | |||
| + | <span style="color:green">'''''2ºcaso'''''</span> - '''''São conhecidos dois lados e o ângulo por eles formado''''' | ||
| + | |||
| + | Considerando \(a\) e \(b\) os dois lados conhecidos e \(C\) o ângulo conhecido, determinamos o lado \(c\) através da lei dos cossenos, \(c^2=a^2+b^2-2ab \, \cos C\). Em seguida, através da lei dos senos determinamos \(\sin A\) e \(\sin B\), \(\displaystyle \sin A=\frac{a \sin C}{c}\) e \(\displaystyle \sin B=\frac{b \sin C}{c}\). | ||
| + | |||
| + | <u>Exemplo</u>: | ||
| + | {| border="0" cellspacing="0" | ||
| + | |- | ||
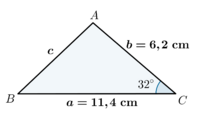
| + | | Conhecidos \(a=11,4 \mbox{ cm}\), \(b=6,2 \mbox{ cm}\) e \(C=32º\) temos então que: | ||
| + | |||
| + | Cálculo de \(c\): \(\quad \quad c^2=a^2+b^2-2ab \, \cos C \, \Leftrightarrow \, c^2=(11,4)^2+(6,2)^2-2\times 11,4 \times 6,2 \times \cos 32º \, \Leftrightarrow \, c \simeq 6,97 \mbox{ cm}\). | ||
| + | |||
| + | Cálculo de \(A\) e \(B\): \(\displaystyle \quad \sin A=\frac{a \, \sin C}{c} \, \Leftrightarrow \, \sin A=\frac{11,4 \times \sin 32º}{6,97} \, \Leftrightarrow \, \sin A \simeq 0,87 \, \Leftrightarrow \, A \simeq 60º\,27'36' '\) | ||
| + | |||
| + | \(\displaystyle \quad \sin B=\frac{b \, \sin C}{c} \, \Leftrightarrow \, \sin B=\frac{6,2 \times \sin 32º}{6,97} \, \Leftrightarrow \, \sin B \simeq 0,47 \, \Leftrightarrow \, B \simeq 28º\,1'48 ' '\) | ||
| + | || | ||
| + | [[Imagem:Resolex6.png|thumb|right|200px|Exemplo 6]] | ||
| + | |} | ||
| + | |||
| + | <span style="color:green">'''''3ºcaso'''''</span> - '''''São conhecidos os três lados''''' | ||
| + | |||
| + | Conhecidos os três lados \(a\), \(b\) e \(c\) utilizamos a [[Lei dos cossenos| lei dos cossenos]] para determinar cada um dos ângulos internos do triângulo. | ||
| + | |||
| + | <u>Exemplo</u>: | ||
| + | {| border="0" cellspacing="0" | ||
| + | |- | ||
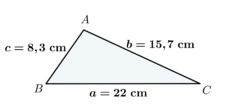
| + | | Sabendo que \(a=22 \mbox{ cm}\), \(b=15,7 \mbox{ cm}\) e \(c=8,3 \mbox{ cm}\) pela lei dos cossenos temos então que: | ||
| + | |||
| + | |||
| + | \(a^2=b^2+c^2-2bc \, \cos A \, \Leftrightarrow \, 22^2={15,7}^2+{8,3}^2-2 \times 15,7 \times 8,3 \, \cos A \, \Leftrightarrow \, \cos A \simeq 0,65 \, \Rightarrow \, A \simeq 130\,º25'48' '\) | ||
| + | |||
| + | |||
| + | \(b^2=a^2+c^2-2ac \, \cos B \, \Leftrightarrow \, {15,7}^2=22^2+{8,3}^2-2 \times 22 \times 8,3 \, \cos B \, \Leftrightarrow \, \cos B \simeq 0,84 \, \Rightarrow \, B \simeq 32\,º58'12' '\) | ||
| + | |||
| + | |||
| + | \(c^2=a^2+b^2-2ab \, \cos C \, \Leftrightarrow \, {8,3}^2=22^2+{15,7}^2-2 \times 22 \times 15,7 \, \cos C \, \Leftrightarrow \, \cos C \simeq 0,96 \, \Rightarrow \, C \simeq 16\,º43'12' '\) | ||
| + | |||
| + | || | ||
| + | [[Imagem:Resolex7.png|thumb|right|230px|Exemplo 7]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | <span style="color:green">'''''4ºcaso'''''</span> - '''''São conhecidos dois lados do triângulo e o ângulo oposto a um deles''''' | ||
| + | |||
| + | Suponhamos que são conhecidos os lados \(a\) e \(b\) e o ângulo \(A\). Utilizamos a [[Lei dos senos| lei dos senos]] para determinar o ângulo \(B\), em seguida, usando o facto da soma dos ângulos internos de um triângulo ser igual a \(180º\) calculamos a amplitude de \(C\). Por fim, determinamos o terceiro lado do triângulo, lado \(c\), através da [[Lei dos cossenos| lei dos cossenos]] (como no 2ºcaso). | ||
| + | |||
| + | <u>Exemplo</u>: | ||
| + | {| border="0" cellspacing="0" | ||
| + | |- | ||
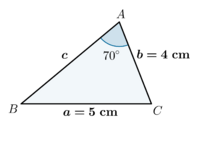
| + | | Conhecidos \(a=10 \mbox{ cm}\), \(b=4 \mbox{ cm}\) e \(A=70º\) temos então que: | ||
| + | |||
| + | |||
| + | \(\displaystyle \frac{a}{\sin A}=\frac{b}{\sin B} \, \Leftrightarrow \, \sin B=\frac{4 \times \sin 70º}{10} \, \Leftrightarrow \, \sin B \simeq 0,38 \, \Leftrightarrow \, B \simeq 22,08º=22\,º4'48' '\) | ||
| + | |||
| + | |||
| + | \(C=180º-(A+B) \, \Leftrightarrow \, C=180º-(70º+22,08º) \, \Leftrightarrow \, C = 87,92º=87\,º55'12' ' \) | ||
| + | |||
| + | |||
| + | \(c^2=a^2+b^2-2ab \cos C \, \Leftrightarrow \, c^2=10^2+4^2-2 \times 10 \times 4 \times \cos{87,92} \, \Leftrightarrow \, c \simeq 10,63 \mbox{ cm} \) | ||
| + | |||
| + | || | ||
| + | [[Imagem:Resolex8.png|thumb|right|210px|Exemplo 8]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | ==Referências== | ||
| + | |||
| + | # J. Jorge G. Calado (1974) ''"Compêndio de Trigonometria"'' 4ªedição. Liv. Popular de Francisco Franco, Lisboa. | ||
| + | ---- <br>Criada em 19 de Fevereiro de 2013<br> Revista em 23 de Março de 2013<br> Aceite pelo editor em 30 de Setembro de 2017<br> | ||
[[Category:Matemática]] | [[Category:Matemática]] | ||
Edição actual desde as 09h34min de 14 de julho de 2021
Referência : Tavares, J., Geraldo, A., (2017) Resolução de triângulos, Rev. Ciência Elem., V5(3):079
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.079]

Índice |
O que é resolver um triângulo
Em qualquer triângulo podemos considerar como elementos principais os seus três lados e os três ângulos internos e todos os outros elementos como elementos secundários, como por exemplo, as alturas, as medianas, o raio do círculo circunscrito, etc.
A resolução de triângulos consiste em determinar alguns elementos do triângulo a partir de elementos já conhecidos. Quando se diz determinar os elementos entenda-se determinar a medida desses elementos.
Resolução de triângulos retângulos
Relações entre os seus elementos
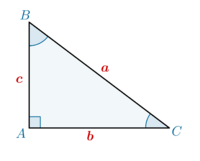
Considerando um triângulo retângulo \([ABC]\) e designemos por \(a\), \(b\) e \(c\) os lados desse triângulo e por \(A\), \(B\) e \(C\) os seus ângulos internos opostos a cada um dos lados, respetivamente (Fig.1).
Estes seis elementos do triângulo satisfazem relações importantes, tais como (considerando \(A=90º\)):
| \[a^2=b^2+c^2 \quad \] | (Teorema de Pitágoras) |
| \[B+C=90º \quad \] | (ângulos complementares) |
Pelas definições de seno e cosseno de um ângulo agudo sabemos que \(\displaystyle \sin B= \frac{b}{a}\) e \(\displaystyle \cos B= \frac{c}{a}\) donde resulta que, \(b=a \, \sin B \,\) e \(c= a \, \cos B\).
Como \(B\) e \(C\) são ângulos complementares temos ainda que \(\sin B= \cos C\) e que \(\cos B= \sin C\), passando as fórmulas anteriores a serem equivalentes a \(b=a \, \cos C\) e \(c= a \, \sin C\), respetivamente.
Resolução de triângulos retângulos
Sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Como estamos a considerar triângulos retângulos um dos ângulos já é conhecido, o ângulo reto, por isso bastam mais dois elementos. Existem assim quatro casos possíveis.
1ºcaso - São conhecidos a hipotenusa e um ângulo agudo
Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, usamos as fórmulas \(b=a \, \sin B\) e \(c=a \, \cos B\) para determinar o comprimento dos dois catetos.
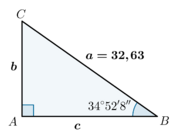
| Exemplo:
Sabendo que a hipotenusa \(a=32,63 \mbox{ cm}\) e que o ângulo agudo \(B=34º\,52' \,8' '\), temos então que: Cálculo de \(C\): \(\qquad C=90º-(34º\,52' \,8' ')=55º\,7' \,52' '\) Cálculo do comprimento dos catetos: \(b=a \, \sin B \, \Leftrightarrow \, b=32,63 \times \sin (55º\,7' \,52' ') \, \Leftrightarrow \, b \simeq 26,77 \mbox{ cm}\) \(c=a \, \cos B \, \Leftrightarrow \, c=32,63 \times \cos (55º\,7' \,52' ') \, \Leftrightarrow \, c \simeq 18,65 \mbox{ cm}\) |
2ºcaso - São conhecidos um cateto e um ângulo agudo
Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de \(B\) e \(C\) serem ângulos complementares. Em seguida, considerando o ângulo oposto ao cateto conhecido, sabemos que o seno desse ângulo é igual ao quociente entre o cateto conhecido (cateto oposto) e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o seno desse ângulo. Ou, se considerarmos o ângulo agudo cujo cateto adjacente é o cateto conhecido, sabemos que o cosseno desse ângulo é igual ao quociente entre o cateto conhecido e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o cosseno desse ângulo. Para determinar o terceiro lado do triângulo usamos o Teorema de Pitágoras.
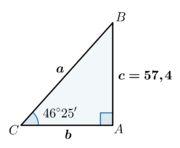
| Exemplo:
Conhecidos o cateto \(c=57,4 \mbox{ cm}\) e o ângulo agudo \(C=46º\, 25'\) temos então que: Cálculo de \(B\): \(B=90º-(46º\, 25')=43º\,35'\)
\(\displaystyle \sin C=\frac{c}{a} \, \Leftrightarrow \, a=\frac{57,4}{\sin(46º\, 25')} \, \Leftrightarrow \, a \simeq 79,24 \mbox{ cm}\) \(a^2=b^2+c^2 \, \Leftrightarrow \, (79,24)^2=b^2+(57,4)^2 \, \Leftrightarrow \, b \simeq 54,63 \mbox{ cm}\) |
3ºcaso - São conhecidos a hipotenusa e um cateto
Para determinarmos o comprimento do terceiro lado do triângulo usamos diretamente o Teorema de Pitágoras. Conhecidos os três lados do triângulo, utilizamos as razões trigonométricas para determinar a amplitude de cada um dos ângulos agudos.
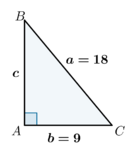
| Exemplo:
Conhecidos a hipotenusa \(a=18 \mbox{ cm}\) e o cateto \(b=9 \mbox{ cm}\) temos então que: Cálculo do segundo cateto utilizando o T.Pitágoras: \(a^2=b^2+c^2 \, \Leftrightarrow \, 18^2=9^2+c^2 \, \Leftrightarrow \, c \simeq 15,59 \mbox{ cm}\) Determinação das amplitudes dos dois ângulos agudos: \(\displaystyle \sin B=\frac{b}{a} \, \Leftrightarrow \, \sin B=\frac{9}{18} \, \Leftrightarrow \, B={\sin}^{-1} (0,5)=30º\) \(C=90º-B \, \Leftrightarrow \, C=90º-30º=60º\) |
4ºcaso - São conhecidos os dois catetos
O comprimento da hipotenusa pode ser determinado através do Teorema de Pitágoras. Para se determinar a amplitude de cada um dos ângulos agudos usamos uma das razões trigonométricas.
| Exemplo:
Conhecidos o cateto \(b=22,6 \mbox{ cm}\) e o cateto \(c=13,5 \mbox{ cm}\) temos então que: Cálculo da hipotenusa utilizando o T.Pitágoras: \(a^2=b^2+c^2 \, \Leftrightarrow \, a^2=(22,6)^2+(13,5)^2 \, \Leftrightarrow \, a \simeq 26,33 \mbox{ cm}\) Determinação das amplitudes dos dois ângulos agudos: \(\displaystyle \tan B=\frac{b}{c} \, \Leftrightarrow \, \tan B=\frac{22,6}{13,5} \, \Leftrightarrow \, B={\tan}^{-1} \left(\frac{22,6}{13,5}\right) \, \Leftrightarrow \, B \simeq 59º \, 8'\, 54' '\) \(C=90º-B \, \Leftrightarrow \, C=90º-(59º \, 8'\, 54' ')=30º \, 51'\, 6' '\) |
Resolução de triângulos quaisquer
Relações entre os seus elementos
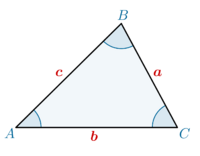
Considerando um triângulo obliquângulo (sem nenhum ângulo reto) \([ABC]\) e designemos por \(a\), \(b\) e \(c\) os lados desse triângulo e por \(A\), \(B\) e \(C\) os seus ângulos internos opostos a cada um dos lados, respetivamente (Fig.2).
Os seis elementos deste triângulo satisfazem relações importantes, tais como:
| \(A+B+C=180º \quad \) | (soma das amplitudes dos ângulos internos de um triângulo) |
| \[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} \quad \] | (Lei dos senos) |
| \(a^2=b^2+c^2-2bc \, \cos A \quad \) ou \(b^2=a^2+c^2-2ac \, \cos B \quad \) ou \(c^2=a^2+b^2-2ab\, \cos C \quad \) | (Lei dos cossenos) |
Resolução de triângulos obliquângulos
As relações estabelecidas anteriormente permitem resolver um triângulo obliquângulo conhecidos alguns dos seus elementos. Já sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Assim podemos considerar quatro casos.
1ºcaso - São conhecidos dois ângulos e um lado
Neste caso, para determinar a amplitude do ângulo desconhecido usa-se o facto da soma das amplitudes dos ângulos internos de um triângulo ser \(180º\). Assim, considerando \(A\) o ângulo desconhecido temos que \(A=180º-(B+C)\). Para determinarmos os lados \(b\) e \(c\), considerando \(a\) conhecido, usamos a lei dos senos. Aplicando esta lei temos então que:
\(\displaystyle \frac{b}{\sin B}=\frac{a}{\sin A} \, \Leftrightarrow \, b=\frac{a \, \sin B}{\sin A}\) e \(\displaystyle \frac{c}{\sin C}=\frac{a}{\sin A} \, \Leftrightarrow \, c=\frac{a \, \sin C}{\sin A}\).
| Exemplo:
Sabendo que \(B=44º\), \(C=76º\) e que \(a=5 \mbox{ cm}\) temos então que: Cálculo de \(A\): \(\quad \quad A=180º-(B+C)=180º-(44º+76º)=60º\). Cálculo de \(b\) e \(c\): \(\quad \quad \displaystyle b=\frac{a\, \sin B}{\sin A}=\frac{5 \times \sin 44º}{\sin 60º} \simeq 4,01 \mbox{ cm} \quad \quad\) e \(\quad \quad \displaystyle c=\frac{a\, \sin C}{\sin A}=\frac{5 \times \sin 76º}{\sin 60º} \simeq 5,6 \mbox{ cm} \) |
2ºcaso - São conhecidos dois lados e o ângulo por eles formado
Considerando \(a\) e \(b\) os dois lados conhecidos e \(C\) o ângulo conhecido, determinamos o lado \(c\) através da lei dos cossenos, \(c^2=a^2+b^2-2ab \, \cos C\). Em seguida, através da lei dos senos determinamos \(\sin A\) e \(\sin B\), \(\displaystyle \sin A=\frac{a \sin C}{c}\) e \(\displaystyle \sin B=\frac{b \sin C}{c}\).
Exemplo:
| Conhecidos \(a=11,4 \mbox{ cm}\), \(b=6,2 \mbox{ cm}\) e \(C=32º\) temos então que:
Cálculo de \(c\): \(\quad \quad c^2=a^2+b^2-2ab \, \cos C \, \Leftrightarrow \, c^2=(11,4)^2+(6,2)^2-2\times 11,4 \times 6,2 \times \cos 32º \, \Leftrightarrow \, c \simeq 6,97 \mbox{ cm}\). Cálculo de \(A\) e \(B\): \(\displaystyle \quad \sin A=\frac{a \, \sin C}{c} \, \Leftrightarrow \, \sin A=\frac{11,4 \times \sin 32º}{6,97} \, \Leftrightarrow \, \sin A \simeq 0,87 \, \Leftrightarrow \, A \simeq 60º\,27'36' '\) \(\displaystyle \quad \sin B=\frac{b \, \sin C}{c} \, \Leftrightarrow \, \sin B=\frac{6,2 \times \sin 32º}{6,97} \, \Leftrightarrow \, \sin B \simeq 0,47 \, \Leftrightarrow \, B \simeq 28º\,1'48 ' '\) |
3ºcaso - São conhecidos os três lados
Conhecidos os três lados \(a\), \(b\) e \(c\) utilizamos a lei dos cossenos para determinar cada um dos ângulos internos do triângulo.
Exemplo:
| Sabendo que \(a=22 \mbox{ cm}\), \(b=15,7 \mbox{ cm}\) e \(c=8,3 \mbox{ cm}\) pela lei dos cossenos temos então que:
|
4ºcaso - São conhecidos dois lados do triângulo e o ângulo oposto a um deles
Suponhamos que são conhecidos os lados \(a\) e \(b\) e o ângulo \(A\). Utilizamos a lei dos senos para determinar o ângulo \(B\), em seguida, usando o facto da soma dos ângulos internos de um triângulo ser igual a \(180º\) calculamos a amplitude de \(C\). Por fim, determinamos o terceiro lado do triângulo, lado \(c\), através da lei dos cossenos (como no 2ºcaso).
Exemplo:
| Conhecidos \(a=10 \mbox{ cm}\), \(b=4 \mbox{ cm}\) e \(A=70º\) temos então que:
|
Referências
- J. Jorge G. Calado (1974) "Compêndio de Trigonometria" 4ªedição. Liv. Popular de Francisco Franco, Lisboa.
Criada em 19 de Fevereiro de 2013
Revista em 23 de Março de 2013
Aceite pelo editor em 30 de Setembro de 2017