Módulo de um número complexo
Referência : Carreira, A., (2015) Módulo de um número complexo, Rev. Ciência Elem., V3(3):174
Autores: Adelaide Carreira
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.174]
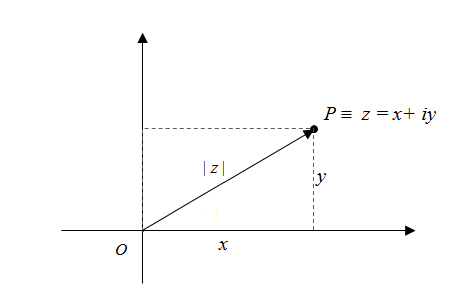
O módulo de um número complexo \(z=x+iy\) é o número real não negativo \(|z| = \sqrt{x^{2} + y^{2}}\).
Exemplo
Se \(z=4+3i\), \(|z|=\sqrt{4^{2} + 3^{2}} =\sqrt{25} =5\)
Nota
Identificando o número complexo \(z=x+iy\) com o seu afixo \(P\) e considerando o vetor posição de \(P\), \( \overrightarrow{OP}\), o módulo de z coincide com a norma de \( \overrightarrow{OP}\).
Propriedades do módulo de um número complexo
Para quaisquer números complexos \(z\) e \(w\) tem-se
- \(|z\cdot w| = |z|\cdot|w|\)
- \(\displaystyle \left | \frac{z}{w} \right | = \frac{\left | z \right | }{\left | w \right | }\), se \(w\neq 0\)
- \(|Re(z)|\leq |z|\) e \(|Im(z)|\leq |z| \)
- \(|z+w|\leq |z|+|w|\)
- \(|z-w|\geq |z|-|w| \)
- \(|z|^{2}=z\times \bar{z}\)
Ver
Criada em 28 de Maio de 2012
Revista em 06 de Junho de 2012
Aceite pelo editor em 07 de Junho de 2012