Estatística
Referência : Martins, E.G.M., (2015) Estatística, Rev. Ciência Elem., V3(2):032
Autores: Maria Eugénia Graça Martins
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.032]

estatísticas, de um modo geral no plural, refere-se a uma enumeração.
estatística, é uma função da amostra.
Estatística, é a ciência que trata da recolha, organização e interpretação de dados, com vista à tomada de decisões, numa situação de incerteza.
O termo Estatística pode ser interpretado de formas distintas. Veja-se PESTANA e VELOSA (2010), página 28 “Estatística, em sentido restrito, é uma enumeração, como quando se fala nas estatísticas da energia, da educação, etc. Num sentido técnico, uma estatística é simplesmente uma função da amostra, que se utiliza para estimar um parâmetro. É nesse sentido que se utiliza a estatística média para estimar o parâmetro valor médio. Uma estatística depende apenas das observações, não depende de parâmetros desconhecidos. Num sentido mais lato, Estatística é a ciência que se ocupa da recolha de informação ou da produção da informação relevante, a fim de a descrever, modelar e a partir dela inferir e predizer. Com mais generalidade ainda, podemos afirmar que a Estatística é a ciência que nos guia na tomada de decisões em situação de incerteza”.
No que se segue vamo-nos debruçar sobre o termo estatística como função dos valores da amostra.
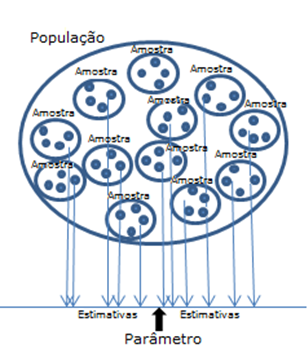
Quando se pretende estimar (obter um valor aproximado de) uma característica numérica da população a que se dá o nome de parâmetro, considera-se uma estatística, que é uma função que só depende dos valores da amostra, a que se dá o nome de estimador do parâmetro em estudo. Ao valor desta função a que chamámos estimador, calculada para uma determinada amostra observada, chamamos estimativa. Também se utiliza o termo estatística como significado de estimativa.
Surge assim o conceito de estatística, que é uma característica numérica da amostra, por oposição a parâmetro, que é característica numérica da população. Estas quantidades são conceptualmente distintas, pois enquanto a característica populacional ou parâmetro, pode ser considerada um valor exato, embora (quase sempre) desconhecido, a característica amostral ou estatística, pode ser calculada, embora difira de amostra para amostra, mas que todavia pode ser considerada uma estimativa útil da característica populacional respetiva.
Por exemplo, se se pretender averiguar o salário médio dos portugueses, recolhe-se uma amostra de alguns salários e calcula-se a média. Este valor é uma estimativa do parâmetro salário médio ou valor médio da variável aleatória “Salário de um português escolhido ao acaso” ou ainda valor médio da população constituída por todos os salários dos portugueses (identificámos variável aleatória com população). Se recolhermos outra amostra de salários, da mesma dimensão, e calcularmos a média, obtemos outra estimativa para o parâmetro em estudo. A média, como função de todas as amostras possíveis (da mesma dimensão) que se podem extrair da população dos indivíduos que auferem um salário, é uma variável aleatória. É a esta variável aleatória que chamamos estimador e ao valor observado, para uma amostra observada, chamamos estimativa.
A utilização do termo estatística tanto para a variável aleatória, como para o valor observado dessa variável aleatória (para uma determinada amostra), pode dar azo a confusões, pelo que de preferência deveriam ser utilizados, respetivamente, os termos estimador e estimativa.
Quando se pretende recolher uma amostra de uma população, podemos recorrer a vários processos de amostragem. Como o nosso objetivo é, a partir das propriedades estudadas na amostra, inferir propriedades para a população, gostaríamos de obter processos de amostragem que deem origem a “bons” estimadores e consequentemente “boas” estimativas. O estudo de um estimador – função de amostras de dimensão n, é feito a partir da sua distribuição de amostragem, ou seja, da distribuição dos valores obtidos pelo estimador, quando se consideram todas as amostras diferentes de dimensão n, utilizando um determinado esquema de amostragem. Tantas as amostras diferentes (2 amostras da mesma dimensão serão diferentes se diferirem pelo menos num dos elementos) que se puderem obter da população, tantas as estimativas eventualmente diferentes que se podem calcular para o parâmetro, mas apresentando, todavia, um determinado padrão.
Distribuição de amostragem de um estimador (ou estatística) é a distribuição dos valores que o estimador assume para todas as possíveis amostras, da mesma dimensão, que se podem selecionar da população.
Como se comportam todas estas estimativas, relativamente ao parâmetro, em estudo? A resposta é dada estudanto a distribuição de amostragem do estimador. Uma vez escolhido um plano de amostragem aleatório, ao pretendermos estimar um parâmetro, pode ser possível utilizar vários estimadores diferentes. Por exemplo, quando pretendemos estudar a variabilidade presente numa população (identificada com a variável aleatória em estudo), que pode ser medida pela variância populacional \(\sigma^{2}\), podemos a partir de uma amostra recolhida \({{\rm{(x_{1}, x_{2}, ..., x_{n})}}}\), obter duas estimativas diferentes para essa variância, utilizando as expressões
\[{{\rm{s}}^2} = \frac{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{{\rm{(}}{{\rm{x}}_{\rm{i}}} - {{\rm{\bar x}}}{\rm{)}}}^{\rm{2}}}} }}{{{\rm{n}} - {\rm{1}}}}{\rm{\quad \quad \quad e \quad \quad \quad }}{{\rm{s}}^{'2}} = \frac{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{{\rm{(}}{{\rm{x}}_{\rm{i}}} - {{\rm{\bar x}}}{\rm{)}}}^{\rm{2}}}} }}{{\rm{n}}}\]
Quais as razões que nos podem levar a preferir uma das estimativas relativamente à outra? Qual o estimador preferido? O que fornece a estimativa \({{\rm{s^{2}}}}\) ou a estimativa \({{\rm{s^{'2}}}}\)? Um critério que costuma ser aplicado é o de escolher um “bom” estimador como sendo aquele que é centrado e que tenha uma boa precisão. Escolhido um plano de amostragem, define-se:
Estimador centrado Um estimador diz-se centrado quando a média das estimativas obtidas para todas as amostras possíveis (da mesma dimensão) que se podem extrair da população, segundo o esquema de amostragem considerado, coincide com o parâmetro a estimar. Quando se tem um estimador centrado, também se diz que é não enviesado.
Uma das razões que nos levam a preferir o estimador \({{\rm{S^{2}}}}\) que fornece as estimativas \({{\rm{s^{2}}}}\) é o facto de ser centrado, quando se utiliza um esquema de amostragem com reposição. Como já se referiu que um estimador é uma variável aleatória, podemos dizer que um estimador centrado é aquele em que o seu valor médio coincide com o parâmetro a estimar. Pode-se mostrar que \(E({{\rm{S^{2}}}})= \sigma^{2}\). No caso da variável aleatória média representada por \({{\rm{\bar X}}}\), também se pode mostrar que \(E(\bar{X)}=\mu\) (valor médio da população em estudo).
Por outro lado, temos que ter outra preocupação com o estimador escolhido, que diz respeito a precisão.
Quando utilizamos um estimador para estimar um parâmetro, e calculamos o seu valor para várias amostras, obtêm-se outras tantas estimativas. Estas estimativas não são iguais devido à variabilidade presente na amostra. Se, no entanto, estas estimativas estiverem próximas, e o estimador for centrado, podemos ter confiança de que a estimativa obtida a partir da amostra recolhida (na prática recolhe-se uma única amostra) está próxima do valor do pârametro (desconhecido) a estimar.
Estimador consistente é aquele em que a variabilidade da sua distribuição de amostragem diminui, à medida que aumenta a dimensão da amostra.
No caso da média pode-se mostrar que \(Var({{\rm{\bar X}}})\) diminui à medida que a dimensão da amostra aumenta. Assim, a média é um estimador centrado e consistente do parâmetro valor médio. Outro exemplo é a proporção amostral - Para saber mais consultar GRAÇA MARTINS (2008).
Referências
1. GRAÇA MARTINS, M. E. (2008) Curso Introdutório Inferência Estatística, em (http://www.alea.pt/index.php?option=com_content&view=article&id=133:introducao-a-inferencia-estatistica&catid=94&lang=pt&Itemid=1205).
2. PESTANA, D., VELOSA, S. (2010) – Introdução à Probabilidade e à Estatística, Volume I, 4ª edição, Fundação Calouste Gulbenkian. ISBN: 978-972-31-1150-7.
Criada em 05 de Março de 2012
Revista em 05 de Junho de 2012
Aceite pelo editor em 06 de Junho de 2012