Raízes de números complexos
Referência : Tavares, J.N., Geraldo, A., (2013) Raízes de números complexos, Rev. Ciência Elem., V1(1):062
Autores: João Nuno Tavares e Ângela Geraldo
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2013.062]

Índice |
Definição
As raízes de índice \(n \in \mathbb{N}\) de um número complexo \(w\) são os números complexos \(z\) tais que \(z^{n}=w\).
Portanto, calcular \(\sqrt[n]{w}\) é equivalente a calcular os números complexos cuja potência de índice \(n\) seja igual a \(w\).
Raízes de índice \(n\)
Determinar as raízes de índice \(n \in \mathbb{N}\) de um número complexo \(w\), ou seja calcular \(\sqrt[n]{w}\) é então equivalente a determinar os números complexos \(z\) tais que:
\(z^n=w\)
Para isso consideramos os números complexos \(z\) e \(w\) na forma polar:
\(w=|w|\,cis\,\alpha\)
\(z=|z|\,cis\,\theta\)
Usando a fórmula de De Moivre temos então que
\(\displaystyle z^n=w \quad \Leftrightarrow \quad (|z|\,cis\,\theta)^n=|w|\,cis\,\alpha \quad \Leftrightarrow \quad |z|^n\,cis\,(n\theta)=|w|\,cis\,\alpha\)
Resolvendo a equação temos, atendendo à igualdade dos números complexos escritos na forma polar, que
\(|z|^n=|w| \Longrightarrow \,|z|=\sqrt[n]{w}=|w|^{1/n}\)
e
\(\displaystyle n\theta=\alpha+2k\pi \, \Longleftrightarrow \, \theta=\frac{\alpha}{n}+\frac{2k\pi}{n} , \quad k=0,1,2,\dots,n-1\).
Portanto, as \(n\) raízes distintas de índice \(n\) de um número complexo \(w=a+bi=|w|\,cis\,\alpha\) são dadas por:
\(\displaystyle z_{k}=|w|^{1/n}\, cis\left(\frac{\alpha}{n}+\frac{2k\pi}{n}\right) , \quad k=0,1,2,\dots,n-1\) (1),
logo têm o mesmo módulo pelo que pertencem à circunferência de centro na origem no referencial e raio \(|z|=|w|^{1/n}\). Note-se ainda que a diferença entre os argumentos de duas raízes \(z_k\) e \(z_{k+1}\), \(\quad k=0,1,2,\dots,n-1\), é \(\displaystyle \frac{2k\pi}{n}\), logo, as \(n\) raízes situam-se nos vértices de um polígono regular de \(n\) lados inscritos na referida circunferência.
| Aplicação 1
Extração de raízes de indíce \(n\) do número complexo \(w\). Escolha o número complexo \(w\) movendo o ponto a azul, escolha \(n\) o índice da raiz no seletor lateral, em seguida clique no botão play para iniciar a animação. Use a caixa de verificação para exibir ou não o polígono de raízes. |
Exemplos
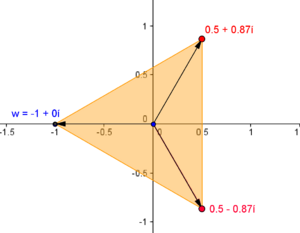
Raízes cúbicas de -1
Considerando \(w=-1\) queremos então determinar \(\sqrt[3]{-1}\), ou seja, encontrar os números complexos \(z=|z|\,cis\,\theta\) tal que \(z^3=w\), isto é, \(z^3 = -1\).Para isso temos de escrever \(w = -1\) na forma polar:
\(-1=|w|\,cis\,\alpha \,\Longleftrightarrow \, -1=|w|\cos\alpha+i\,|w|\sin\alpha \, \Longleftrightarrow \)
\(\Longleftrightarrow\, |w|\cos\alpha=-1 \,\wedge \,|w|\sin\alpha =0 \,\Longleftrightarrow\, \, |w|=1 \,\wedge\, \alpha=\pi\)
Portanto, \(w=\, cis\, \pi\).
Aplicando a fórmula (1) obtemos três raízes cujo módulo é \(\displaystyle |z|=\sqrt[3]{1}=1 \,\) e argumento \(\displaystyle \theta_k=\frac{\pi}{3}+\frac{2k\pi}{3} \, , \quad k=0,1,2\), isto é,
\(\displaystyle |z|=1 \, \wedge \, \left(\theta=\frac{\pi}{3} \, \vee \, \theta=\pi \, \vee \, \theta=\frac{5\pi}{3}\right) \)
As raízes cúbicas de \(-1\) são então:
\(z_0\) \(\displaystyle =\, cis\, \left(\frac{\pi}{3}\right)=\frac{1}{2}+\frac{\sqrt{3}}{2}i \, ; \quad \) \(z_1\) \(\displaystyle=\, cis\, \pi=-1 \, ; \quad \) \(z_3\) \(\displaystyle =\, cis\, \left(\frac{5\pi}{3}\right)=\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
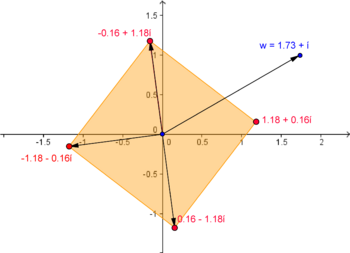
Raízes de índice 4 de \(w=\sqrt{3}+i\)
Considerando \(w=\sqrt{3}+i\) pretendemos determinar \(\sqrt[4]{\sqrt{3}+i}\), ou seja, encontrar os números complexos \(z=|z|\,cis \,\theta\) tais que \(z^4=w\).
Mais uma vez precisamos de escrever \(w\) na sua forma polar:
\(\sqrt{3}+i=|w|\,cis\,\alpha \,\Longleftrightarrow \, \sqrt{3}=|w|\cos\alpha \, \wedge \, 1=|w|\sin\alpha \, \Longleftrightarrow \)
\(\displaystyle \Longleftrightarrow |w|=\frac{\sqrt{3}}{\cos\alpha} \, \wedge \, |w|=\frac{1}{\sin\alpha}\)
\(|w| = \sqrt{\left(\sqrt{3}\right)^2 + 1} = \sqrt{4} = 2\) e \(\sqrt{3} + i = 2 cis\alpha = 2\cos\alpha + 2i\sin\alpha\)
Então,
| \(\displaystyle 2\cos\alpha = \sqrt{3} \Longleftrightarrow \cos\alpha = \frac{\sqrt{3}}{2}\)
\(\displaystyle 2\sin\alpha = 1 \Longleftrightarrow \sin\alpha = \frac{1}{2}\) |
donde \(\displaystyle\alpha = \frac{\pi}{6}\) |
Portanto, \(\displaystyle w=2\,cis\,\frac{\pi}{6}\).
Aplicando a fórmula (1) temos então que as raízes têm módulo \(\displaystyle |z|=\sqrt[4]{2} \,\) e argumento \(\displaystyle \theta_k =\frac{\pi/6}{4}+\frac{2k\pi}{4} \, , \quad k=0,1,2,3\), isto é, \(\displaystyle |z|=\sqrt[4]{2} \, \wedge \, \left(\theta=\frac{\pi}{24} \, \vee \, \theta=\frac{13\pi}{24} \, \vee \, \theta=\frac{25\pi}{24} \, \vee \, \theta=\frac{37\pi}{24}\right) \)
As raízes de índice 4 de \(\sqrt{3}+i\) são, então:
\(z_0\)\(\displaystyle =\sqrt[4]{2} \, cis\, \left(\frac{\pi}{24}\right) \cong 1,18+0,16i \, ; \quad \) \(z_1\) \(\displaystyle =\sqrt[4]{2} \, cis\, \left(\frac{13\pi}{24}\right) \cong -0,16+1,18i \, ; \quad \) \(z_2\) \(\displaystyle =\sqrt[4]{2} \, cis\, \left(\frac{25\pi}{24}\right) \cong -1,18-0,16i \, ; \quad \) \(z_3\) \(\displaystyle =\sqrt[4]{2} \, cis\, \left(\frac{37\pi}{24}\right) \cong 0,16-1,18i \)
Criada em 12 de Novembro de 2012
Revista em 06 de Maio de 2013
Aceite pelo editor em 06 de Maio de 2013