Resolução de triângulos

Referência : Não citável Esta página ainda não foi aprovada.
Autor: João Nuno Tavares e Ângela Geraldo
Editor: Colocar nome do editor

O que é resolver um triângulo

Em qualquer triângulo podemos considerar como elementos principais os seus três lados e os três ângulos internos e todos os outros elementos como elementos secundários, como por exemplo, as alturas, as medianas, o raio do círculo circunscrito, etc.

A resolução de triângulos consiste em determinar alguns elementos do triângulo a partir de elementos já conhecidos. Quando nos referimos a determinar os elementos queremos dizer determinar a medida desses elementos.

Resolução de triângulos retângulos

Relações entre os seus elementos

Figura 1 - Triângulo retângulo

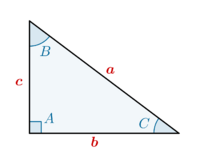
Considerando um triângulo retângulo $[ABC]$ e designemos por $a$, $b$ e $c$ os lados desse triângulo e por $A$, $B$ e $C$ os seus ângulos internos opostos a cada um dos lados, respetivamente (Fig.1).

Estes seis elementos do triângulo satisfazem relações importantes, tais como (considerando $A=90º$):

Pelas definições de seno e cosseno de um ângulo agudo sabemos que $\displaystyle \sin B= \frac{b}{a}$ e $\displaystyle \cos B= \frac{c}{a}$ donde resulta que, $b=a \, \sin B \,$ e $c= a \, \cos B$.

Como $B$ e $C$ são ângulos complementares temos ainda que $\sin B= \cos C$ e que $\cos B= \sin C$, passando as fórmulas anteriores a serem equivalentes a $b=a \, \cos C$ e $c= a \, \sin C$, respetivamente.

Resolução de triângulos retângulos

Sabemos que para definir um triângulo precisamos conhecer três dos seus elementos, sendo um deles necessariamente um lado. Como estamos a considerar triângulos retângulos um dos ângulos já é conhecido, o ângulo reto, por isso bastam mais dois elementos. Exstem assim quatro casos possíveis.

1ºcaso - São conhecidos a hipotenusa e um ângulo agudo

Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de $B$ e $C$ serem ângulos complementares. Em seguida, usamos as fórmulas $b=a \, \sin B$ e $c=a \, \cos B$ para determinar o comprimento dos dois catetos.

Exemplo:

Sabendo que a hipotenusa $a=32,63 \mbox{ cm}$ e que o ângulo agudo $B=34º\,52' \,8' '$, temos então que:

Cálculo de $C$: $\qquad C=90º-(34º\,52' \,8' ')=55º\,7' \,52' '$

Cálculo do comprimento dos catetos:

$b=a \, \sin B \, \Leftrightarrow \, b=32,63 \times \sin (55º\,7' \,52' ') \, \Leftrightarrow \, b \simeq 26,77 \mbox{ cm}$

$c=a \, \cos B \, \Leftrightarrow \, c=32,63 \times \cos (55º\,7' \,52' ') \, \Leftrightarrow \, c \simeq 18,65 \mbox{ cm}$

2ºcaso - São conhecidos um cateto e um ângulo agudo

Neste caso, para determinar a amplitude do ângulo agudo desconhecido, usamos o facto de $B$ e $C$ serem ângulos complementares. Em seguida, considerando o ângulo oposto ao cateto conhecido, sabemos que o seno desse ângulo é igual ao quociente entre o cateto conhecido (cateto oposto) e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o seno desse ângulo. Ou, se considerarmos o ângulo agudo cujo cateto adjacente é o cateto conhecido, sabemos que o cosseno desse ângulo é igual ao quociente entre o cateto conhecido e a hipotenusa, daí resulta que o comprimento da hipotenusa é igual ao quociente entre o cateto e o cosseno desse ângulo. Para determinar o terceiro lado do triângulo usamos o Teorema de Pitágoras.

Exemplo:

Conhecidos o cateto $c=57,4 \mbox{ cm}$ e o ângulo agudo $C=46º\, 25'$ temos então que:

Cálculo de $B$: $B=90º-(46º\, 25')=43º\,35'$

Cálculo do comprimento da hipotenusa e cateto:

$\displaystyle \sin C=\frac{c}{a} \, \Leftrightarrow \, a=\frac{57,4}{\sin(46º\, 25')} \, \Leftrightarrow \, a \simeq 79,24 \mbox{ cm}$

$a^2=b^2+c^2 \, \Leftrightarrow \, (79,24)^2=b^2+(57,4)^2 \, \Leftrightarrow \, b \simeq 54,63 \mbox{ cm}$

3ºcaso - São conhecidos a hipotenusa e um cateto

Para determinarmos o comprimento do terceiro lado do triângulo usamos diretamente o Teorema de Pitágoras. Conhecidos os três lados do triângulo, utilizamos as razões trigonométricas para determinar a amplitude de cada um dos ângulos agudos.

Exemplo:

Conhecidos a hipotenusa $a=18 \mbox{ cm}$ e o cateto $b=9 \mbox{ cm}$ temos então que:

Cálculo do segundo cateto utilizando o T.Pitágoras: $a^2=b^2+c^2 \, \Leftrightarrow \, 18^2=9^2+c^2 \, \Leftrightarrow \, c \simeq 15,59 \mbox{ cm}$

Determinação das amplitudes dos dois ângulos agudos:

$\displaystyle \sin B=\frac{b}{a} \, \Leftrightarrow \, \sin B=\frac{9}{18} \, \Leftrightarrow \, B={\sin}^{-1} (0,5)=30º$

$C=90º-B \, \Leftrightarrow \, C=90º-30º=60º$

4ºcaso - São conhecidos os dois catetos

O comprimento da hipotenusa pode ser determinado através do Teorema de Pitágoras. Para se determinar a amplitude de cada um dos ângulos agudos usamos uma das razões trigonométricas.

Exemplo:

Conhecidos o cateto $b=22,6 \mbox{ cm}$ e o cateto $c=13,5 \mbox{ cm}$ temos então que:

Cálculo da hipotenusa utilizando o T.Pitágoras: $a^2=b^2+c^2 \, \Leftrightarrow \, a^2=(22,6)^2+(13,5)^2 \, \Leftrightarrow \, a \simeq 26,33 \mbox{ cm}$

Determinação das amplitudes dos dois ângulos agudos:

$\displaystyle \tan B=\frac{b}{c} \, \Leftrightarrow \, \tan B=\frac{22,6}{13,5} \, \Leftrightarrow \, B={\tan}^{-1} \left(\frac{22,6}{13,5}\right) \, \Leftrightarrow \, B \simeq 59º \, 8'\, 54' '$

$C=90º-B \, \Leftrightarrow \, C=90º-(59º \, 8'\, 54' ')=30º \, 51'\, 6' '$

Resolução de triângulos quaisquer