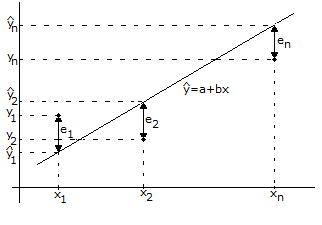Regressão linear simples
Referência : Martins, E.G.M., (2019) Regressão linear simples, Rev. Ciência Elem., V7(3):045
Autor: Maria Eugénia Graça Martins
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2019.045]

Um modelo de Regressão é um modelo matemático que descreve a relação entre duas ou mais variáveis de tipo quantitativo. Se o estudo incidir unicamente sobre duas variáveis e o modelo matemático for a equação de uma reta, então diz-se regressão linear simples.
Quando o diagrama de dispersão realça a existência de uma associação linear entre duas variáveis x e y, então é possível resumir através de uma reta a forma como a variável dependente ou variável resposta (ou variável a prever) y é influenciada pela variável independente ou variável explanatória (ou variável preditora) x. A esta reta dá-se o nome de reta de regressão.
Dado um conjunto de dados bivariados (xi, yi), i=1,...,n, do par de variáveis (x, y), pode ter interesse ajustar uma reta da forma y=a+bx, que dê informação de como se refletem em y as mudanças processadas em x. Um dos métodos mais conhecidos de ajustar uma reta a um conjunto de dados, é o método dos mínimos quadrados, que consiste em determinar a reta que minimiza a soma dos quadrados dos desvios (ou erros) entre os verdadeiros valores das ordenadas e os obtidos a partir da reta, que se pretende ajustar
Esta técnica, embora muito simples, é pouco resistente, já que é muito sensível a dados “estranhos” - valores que se afastam da estrutura da maioria, normalmente designados por outliers. Efetivamente, quando se pretende minimizar
\[\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{\rm{e}}_{_{\rm{i}}}^{\rm{2}}} = \sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{{\rm{(}}{{\rm{y}}_{\rm{i}}} - {{{{\rm{\hat y}}}}_{\rm{i}}}{\rm{)}}}^{\rm{2}}}} \]
pode-se mostrar que os estimadores do declive e da ordenada da origem da reta de regressão são, respetivamente:
\({\rm{b}} = \frac{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{\rm{(}}{{\rm{x}}_{\rm{i}}} - {{\rm{\bar x}}}{\rm{)(}}{{\rm{y}}_{\rm{i}}} - {{\rm{\bar y}}}{\rm{)}}} }}{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{{\rm{(}}{{\rm{x}}_{\rm{i}}} - {{\rm{\bar x}}}{\rm{)}}}^{\rm{2}}}} }}{\rm{ \quad \quad \quad e \quad \quad \quad a = }}{{\rm{\bar y}}}{\rm{ }} - {\rm{ b\bar x}}\)
onde se representa por \({{\rm{\bar x}}}\) e \({{\rm{\bar y}}}\) as médias dos xi’s e dos yi’s. O facto de dependerem da média, que é uma medida não resistente, faz com que a recta de regressão seja também não resistente. Assim, é necessário proceder a uma análise prévia do diagrama de dispersão para ver se não existem alguns outliers. À reta de regressão obtida por este processo, também se dá o nome de reta dos mínimos quadrados.
Pode-se mostrar que \(r^2=1-\frac{{\sum^n_{i=0}{(y_i-\widehat{y_i}})}^2}{{\sum^n_{i=0}{(y_i-{\mathop{y}\limits^{\leftharpoonup}}_i})}^2}\) onde r é o coeficiente de correlação amostral entre x e y. Esta quantidade \({{\rm{r}}^{\rm{2}}}\) é o coeficiente de determinação e é referida como a quantidade de variabilidade dos dados explicada pelo modelo de regressão. Esta medida é normalmente utilizada como uma indicação da adequação do modelo de regressão ao conjunto de pontos inicialmente dado<[1], mas deve ser usada com precaução, pois nem sempre um valor de \(r^{2}\) grande (próximo de 1) é sinal de que um modelo esteja a ajustar bem os dados. Do mesmo modo, um valor baixo de \(r^{2}\), pode ser provocado por um outlier, enquanto a maior parte dos dados se ajustam razoavelmente bem a uma reta[2]. Uma visualização prévia dos dados num diagrama de dispersão é fundamental.
Uma forma de verificar se o modelo ajustado é bom é através dos resíduos, isto é, das diferenças entre os valores observados y e os valores ajustados \({\rm{\hat y}}\):
resíduos = dados observados – valores ajustados
pois se estes não se apresentarem muito grandes, nem com nenhum padrão bem determinado, é sintoma de que o modelo que estamos a ajustar é bom.
Nota
A reta de regressão é utilizada em predições, isto é, para predizer o valor de y, para um dado valor de x. No entanto estas predições não devem contemplar valores de x fora do intervalo dos xi’s, uma vez que o facto de a reta ajustar bem os pontos dados, não significa que sirva para fazer extrapolações.
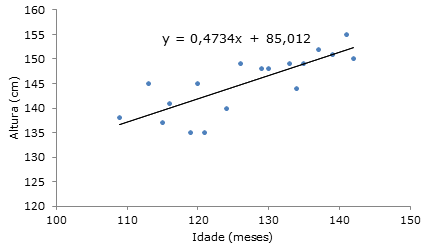
Suponha que se recolheu o seguinte conjunto de dados referentes à idade (em meses) e à altura em centímetros de 18 crianças de uma escola:
O diagrama de dispersão dos dados mostra a existência de uma relação linear entre a idade e a altura, pelo que se vai ajustar aos dados uma reta dos mínimos quadrados, cuja equação está no gráfico seguinte (obtida no Excel):
O coeficiente de correlação é igual a 0,793, donde o coeficiente de determinação vem aproximadamente igual a 63% (≈100x0,7932)%, o que significa que a variabilidade que não é explicada pela reta de regressão anda à volta de 37% (=100-63)%.
Se se tentar extrapolar a altura de um jovem com cerca de 17 anos (200 meses) obter-se-á uma altura de 180 cm e para um jovem adulto de cerca de 21 anos, mais de 2 metros de altura, o que vai de encontro à nota anterior.
Referências
- ↑ GRAÇA MARTINS, M.E. , Introdução à Probabilidade e à Estatística. Com complementos de Excel., Edição da SPE, ISBN- 972-8890-03-6. Depósito Legal 228501/05. 2005.
- ↑ De Veaux, R. D. et al., Intro stats, Pearson Education Inc. ISBN 0-201-70910. 2004.b
3. Montgomery, D. C. & Runger, G. C., Applied statistics and probability for engineers, John Wiley & Sons, Inc. ISBN 0-471-20454-4. 2003.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 25 de Março de 2012
Revista em 16 de Fevereiro de 2019
Aceite pelo editor em 16 de Outubro de 2019