Diferenças entre edições de "Lei dos cossenos"

Da WikiCiências
Share/Save/Bookmark
Ir para: navegação, pesquisa
(Criou nova página com '<span style="font-size:8pt"><b>Referência : </b><font color="#003600" >Não citável</font></span> <span style="font-size:8pt"><font color="red">'''''Esta página ainda n…')
 
 
(19 edições intermédias de 3 utilizadores não apresentadas)
Linha 1: Linha 1:
−
<span style="font-size:8pt"><b>Referência : </b><font color="#003600" >Não citável</font></span>  <span style="font-size:8pt"><font color="red">'''''Esta página ainda não foi aprovada.'''''</font></span>
+
<span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) ''Lei dos cossenos'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(4):084
 
<br>
 
<br>
−
<span style="font-size:8pt"><b>Autor</b>: <i>Colocar nome do autor</i></span><br>
+
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br>
−
<span style="font-size:8pt"><b>Editor</b>: <i>Colocar nome do editor</i></span>
+
<span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usu&aacute;rio:Jfgomes47|José Ferreira Gomes]]</i></span><br>
−
 
+
<span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.084 https://doi.org/10.24927/rce2017.084]]</i></span><br>
−
----
+
<html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-084.pdf" target="_blank">
 +
                <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html>
 
----
 
----
 +
 +
=Lei dos cossenos=
 +
 +
Num [[Triângulo|triângulo]], o quadrado de um lado é igual à soma dos quadrados dos outros dois, menos o dobro do produto desses lados pelo [[Cosseno|cosseno]] do ângulo interno por eles determinado.
 +
 +
 +
Por exemplo, no caso ilustrado no applet
 +
<div style="text-align: center;">
 +
\(a^2=b^2+c^2-2bc \cos\alpha\)
 +
</div>
 +
 +
 +
{| class="wikitable"
 +
|-
 +
| <html><iframe scrolling="no" title="Lei dos cossenos" src="https://www.geogebra.org/material/iframe/id/sfknyqwa/width/300/height/270/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="300px" height=270px" style="border:0px;"> </iframe></html> ||&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;  ||
 +
Eis a demonstração. Considere o triângulo \(ABC\). Seja \(h\) a medida da [[Altura|altura]] relativa ao vértice \(C\) (veja o applet ao lado).
 +
O triângulo \(ADC\) é retângulo em \(D\), e daí que ([[Teorema_de_Pitágoras|teorema de Pitágoras]]).
 +
 +
\(b^2=h^2+AD^2\Longrightarrow h^2=b^2-AD^2\)
 +
 +
Analogamente, o triângulo \(BDC\) é retângulo em \(D\), e daí que (teorema de Pitágoras).
 +
 +
\(a^2=h^2+(BD)^2 \Longrightarrow h^2=a^2-BD^2=a^2-(c-AD)^2 \)
 +
 +
Igualando as duas expressões obtemos
 +
 +
\(b^2-AD^2=a^2-(c-AD)^2=a^2-c^2-AD^2+2c\, AD  \)
 +
 +
e atendendo a que \(AD=b\cos\alpha\), vem finalmente que
 +
 +
<div style="text-align: center;">
 +
\(a^2=b^2+c^2-2bc \cos\alpha\)
 +
</div>
 +
 +
que é a chamada '''lei dos cossenos'''.
 +
 +
É importante notar que \(AD\) tem sinal positivo quando \(D\) está à direita de \(A\), e tem sinal negativo quando \(D\) está à esquerda  de \(A\) (relativamente ao sentido de \(A\) para \(B\)).
 +
|}
 +
 +
=Uma aplicação=
 +
 +
'''Dados''':
 +
 +
* dois [[Círculo|círculos]] no plano, de raios e centros conhecidos, digamos \(\mathcal{C}_1=\mathcal{C}(z_1,R_1)\) e \(\mathcal{C}_2=\mathcal{C}(z_2,R_2)\), que não se intersectam. Portanto, usando notações complexas \(|z_1-z_2| >R_1+R_2\)
 +
 +
* um terceiro círculo \(\mathcal{C}=\mathcal{C}(z,R)\) do qual apenas se conhece o raio \(R\).
 +
 +
'''Problema''': calcular as posições do centro \(z\) de tal forma a que \(\mathcal{C}\) seja [[Círculos_tangentes|tangente]] aos dois círculos dados \(\mathcal{C}_1\) e \(\mathcal{C}_2\).
 +
 +
 +
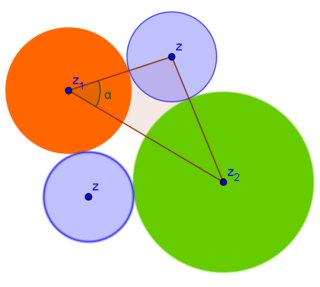
[[Ficheiro:Leicossenos_aplic.png|thumb|right|320px|'''Figura 1''' -  Uma aplicação da lei dos cossenos ]] Um pouco de geometria da [[Multiplicação_e_divisão_de_números_complexos|multiplicação de números complexos]] revela que as duas posições possíveis do centro \(z\) são dadas pela fórmula
 +
 +
\(z=z_1+(R+R_1)\displaystyle\frac{z_2-z_1}{|z_2-z_1|}e^{\pm i\alpha}\)
 +
 +
onde o ângulo \(\alpha\) é determinado pela lei dos cossenos, aplicada ao triângulo de vértices \(z_1,z_2\) e \(z\):
 +
 +
\(a^2=b^2+c^2-2bc \cos\alpha\)
 +
 +
onde
 +
 +
\(a=R+R_2, \ \ \ b=R+R_1, \ \ c=|z_2-z_1|\) 
 +
 +
 +
 +
 +
 +
 +
---- <br>Criada em 10 de Dezembro de 2012<br> Revista em 27 de Fevereiro de 2013<br> Aceite pelo editor em 31 de Dezembro de 2017<br>
 +
[[Category:Matemática]]

Edição actual desde as 11h19min de 19 de julho de 2021

Referência : Tavares, J., Geraldo, A., (2017) Lei dos cossenos, Rev. Ciência Elem., V5(4):084
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.084]
PDF Download

Lei dos cossenos

Num triângulo, o quadrado de um lado é igual à soma dos quadrados dos outros dois, menos o dobro do produto desses lados pelo cosseno do ângulo interno por eles determinado.


Por exemplo, no caso ilustrado no applet

\(a^2=b^2+c^2-2bc \cos\alpha\)


                     

Eis a demonstração. Considere o triângulo \(ABC\). Seja \(h\) a medida da altura relativa ao vértice \(C\) (veja o applet ao lado). O triângulo \(ADC\) é retângulo em \(D\), e daí que (teorema de Pitágoras).

\(b^2=h^2+AD^2\Longrightarrow h^2=b^2-AD^2\)

Analogamente, o triângulo \(BDC\) é retângulo em \(D\), e daí que (teorema de Pitágoras).

\(a^2=h^2+(BD)^2 \Longrightarrow h^2=a^2-BD^2=a^2-(c-AD)^2 \)

Igualando as duas expressões obtemos

\(b^2-AD^2=a^2-(c-AD)^2=a^2-c^2-AD^2+2c\, AD \)

e atendendo a que \(AD=b\cos\alpha\), vem finalmente que

\(a^2=b^2+c^2-2bc \cos\alpha\)

que é a chamada lei dos cossenos.

É importante notar que \(AD\) tem sinal positivo quando \(D\) está à direita de \(A\), e tem sinal negativo quando \(D\) está à esquerda de \(A\) (relativamente ao sentido de \(A\) para \(B\)).

Uma aplicação

Dados:

  • dois círculos no plano, de raios e centros conhecidos, digamos \(\mathcal{C}_1=\mathcal{C}(z_1,R_1)\) e \(\mathcal{C}_2=\mathcal{C}(z_2,R_2)\), que não se intersectam. Portanto, usando notações complexas \(|z_1-z_2| >R_1+R_2\)
  • um terceiro círculo \(\mathcal{C}=\mathcal{C}(z,R)\) do qual apenas se conhece o raio \(R\).

Problema: calcular as posições do centro \(z\) de tal forma a que \(\mathcal{C}\) seja tangente aos dois círculos dados \(\mathcal{C}_1\) e \(\mathcal{C}_2\).


Figura 1 - Uma aplicação da lei dos cossenos
Um pouco de geometria da multiplicação de números complexos revela que as duas posições possíveis do centro \(z\) são dadas pela fórmula

\(z=z_1+(R+R_1)\displaystyle\frac{z_2-z_1}{|z_2-z_1|}e^{\pm i\alpha}\)

onde o ângulo \(\alpha\) é determinado pela lei dos cossenos, aplicada ao triângulo de vértices \(z_1,z_2\) e \(z\):

\(a^2=b^2+c^2-2bc \cos\alpha\)

onde

\(a=R+R_2, \ \ \ b=R+R_1, \ \ c=|z_2-z_1|\)





Criada em 10 de Dezembro de 2012
Revista em 27 de Fevereiro de 2013
Aceite pelo editor em 31 de Dezembro de 2017

Obtida de "https://wikiciencias.casadasciencias.org/wiki/index.php?title=Lei_dos_cossenos&oldid=29724"