O corpo negro
Referência : Lage, E., (2021) O corpo negro, Rev. Ciência Elem., V9(2):027
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2021.027]

Resumo
O desafio lançado por Kirchhoff[1] - qual a expressão da intensidade espectral \(I_{\nu }\left ( T \right )\), i.e., da potência associada com cada “cor” da radiação térmica? - viria a gerar sucessivos contributos quer dos experimentalistas quer dos teóricos. Enormes progressos foram alcançados com a formulação das leis de Stefan-Boltzmann e de Wien, esta reduzindo a expressão da intensidade espectral à determinação de uma única função. Contudo, a forma adequada desta função mostrou-se incompatível com a Física Clássica, originando uma crise que é aqui analisada com algum detalhe.
Stefan (1879) conjetura, com base nos resultados experimentais, que a energia total radiada, em cada segundo, por um corpo varia como a 4.ª potência da sua temperatura absoluta, mas Boltzmann (1884) vem corrigir esta afirmação: a lei é válida para um corpo negro:
\(I\left ( T \right )=\int_{0}^{\infty }d\nu I_{\nu }\left ( T \right )\propto T^{4}\) (1)

Nesta altura da História, já o eletromagnetismo estava bem fundamentado e sabia-se que a radiação não só transporta energia como exerce pressão. Com efeito, em 1884, John Henry Poynting mostra que as equações de Maxwell originam quer uma densidade volúmica de energia eletromagnética (\(u\)) quer uma densidade de fluxo dessa energia (o bem conhecido vetor de Poynting). Estas quantidades satisfazem a um princípio genérico de conservação (“Teorema de Poynting”) e, aplicadas a ondas planas e monocromáticas, movendo- se no vazio, conduzem à relação:
\(I_{\nu }=\frac{c}{4\pi}u_{\nu }\) (2)
onde \(c\) é a velocidade da luz e \(u_{\nu }\) é a densidade espectral de energia, i.e., a energia que, em cada unidade de volume, está associada com as ondas eletromagnéticas de frequências \(\nu \) (a menos de \(d\nu\)). Assim, o resultado estabelecido pela Lei de Stefan eq. (1) pode reescrever-se sob a forma:
\(u=\int_{0}^{\infty }d\nu u\nu =\frac{4\pi}{c}\int_{0}^{\infty }d\nu I_{\nu}=\sigma T^{4}\) (3)
onde, por ajuste com os dados experimentais, se tem \(\sigma =7,62\times 10^{-22}J/m^{3}K^{4}\), conhecida por constante de Stefan-Boltzmann.
Poynting mostrou, também, que ondas eletromagnéticas refletidas por um espelho perfeito, exercem, sobre o espelho, uma pressão, tendo encontrado:
\(p=\frac{1}{3}u\) (4)
Boltzmann (1884) utiliza este resultado para deduzir a Lei de Stefan. Para tal, considera o campo de radiação térmica como um sistema termodinâmico – ele ocupa um dado volume (o volume do espaço rodeado por espelhos totalmente refletores) e está a uma dada temperatura (a temperatura dos corpos que originaram a radiação e estão, com o campo, em equilíbrio térmico). A energia total da radiação é \(U\left ( V,T \right )=Vu\left ( T \right )\) e podemos considerar que esta é toda a energia no volume dado. Com efeito, os corpos ajudam, apenas, a estabelecer o equilíbrio térmico das diferentes radiações, mas podem ser tão pequenos quanto quisermos, pelo que a sua contribuição para a energia pode ser ignorada. Apliquemos, então, a Termodinâmica a tal sistema – somos imediatamente obrigados a reconhecer que o campo de radiação tem uma entropia S. Esta importante conclusão pode ser obtida do seguinte modo – suponhamos que inicialmente o espaço estava vazio e que lá se colocou um corpo à temperatura \(T_{i}\). O corpo arrefece, porque radia, até atingir o equilíbrio térmico com a radiação a uma temperatura \(T < T_{i}\). A entropia do corpo diminui, mas a Segunda Lei da Termodinâmica exige que a entropia total deste sistema isolado (corpo e radiação) aumente, atingindo o seu valor máximo no equilíbrio. Assim, somos forçados a atribuir uma entropia ao campo de radiação, o crescimento da qual compensa o decréscimo da entropia do corpo.

Aplicando os princípios da Termodinâmica a uma transformação reversível, obtemos[2]:
\(dU=TdS-pdV\rightarrow V\left ( du-Tds \right )+dV\left ( u-Ts+p \right )=0\)
onde definimos a densidade volúmica de entropia: \(s\equiv \frac{S}{V}\). Daqui resultam:
\(u=Ts-p\)
\(du=Tds\)
Ora, da energia livre de Helmholtz, \(F = U − TS\), deduzimos:
\(dF=-SdT-pdV\rightarrow s\left ( T \right )=\frac{\partial S}{\partial V}=\frac{dp}{dT}\)
Assim, da primeira das equações anteriores, tem-se:
\(u=T\frac{\partial p}{\partial T}-p\)
Invocando, agora, a eq. (4), reproduzimos a Lei de Stefan:
\(4u=T\frac{du}{dT}\rightarrow u=\sigma T^{4}\)
Adicionalmente, obtemos:
\(\frac{S}{V}=s=\frac{4}{3}\sigma T^{3}\)
Encontramos assim a entropia total do campo de radiação – mas não encontramos como essa entropia se distribui pelas diferentes radiações, com diferentes frequências, que constituem o campo. De forma análoga a \(I_{\nu }\), definimos \(L_{\nu }\) como a entropia transportada pelas radiações com frequência \(\nu\). Naturalmente, designamos \(L_{\nu }\) por intensidade espectral de entropia e, tal como a intensidade espectral de energia, é uma característica de cada feixe da radiação térmica. Ora, da mesma forma que:
\(u=\frac{4\pi}{c}\int_{0}^{-\infty }d\nu I_{\nu }=\sigma T^{4}\)
também, por definição, se tem:
\(s=\frac{4\pi}{c}\int_{0}^{\infty }d\nu L_{\nu }=\sigma T^{3}\)
e tal como \(\frac{ds}{du}=\frac{1}{T}\), obtemos
\(s=\frac{4\pi}{c}\int_{0}^{\infty }d\nu L_{\nu }=\sigma T^{3}\)
e tal como \(\frac{ds}{du}=\frac{1}{T}\)
\(\frac{\partial L_{\nu }}{\partial I_{\nu }}=\frac{1}{T}\) (5)

Um passo importante na determinação de \(L_{\nu }\) foi dado por Wien (1893). Não reproduziremos aqui toda a belíssima análise que efetuou, mas serão indicadas sumariamente as ideias principais. Wien imaginou uma diminuição adiabática do volume ocupado pela radiação e considerou o que se passa junto a uma das paredes, refletor perfeito, por hipótese. Essa parede move-se lentamente; como consequência, a radiação nela incidente com uma frequência \(\nu\) é refletida com uma frequência ligeiramente maior (efeito Doppler). A relação entre a frequência da radiação incidente e a frequência da radiação refletida é bem conhecida. Wien considerou, a seguir, o balanço energético na superfície do espelho – em cada segundo, desaparece energia do feixe incidente porque se refletiu no espelho (alterando a direção de propagação) e aumenta a intensidade da onda refletida. A diferença, que seria nula se o espelho estivesse parado, não é, agora, nula, por duas razões: por um lado, o espelho realiza trabalho contra as forças de pressão e, por outro lado, no seu movimento o espelho rouba volume, diminuindo a energia associada quer com a radiação incidente quer com a radiação refletida. Entrando em conta com todos estes fatores, Wien concluiu que \(\frac{I_{\nu }}{\nu ^{3}}\) permanece constante durante o movimento lento do espelho. Mas sendo lento, a transformação é adiabática e, portanto, a entropia não pode variar. Repetindo a análise feita para a energia (mas com uma simplificação – o movimento do espelho gera trabalho mas não entropia), obtemos outra conclusão: \(\frac{L_{\nu }}{\nu ^{2}}\) deve ser constante. Ora, sendo \(L_{\nu }\) função de \(I_{\nu }\),eq. (5), e permanecendo \(\frac{I_{\nu }}{\nu ^{3}}\) e \(\frac{L_{\nu }}{\nu ^{2}}\) constantes, então deve ser:
\(\frac{L_{\nu }}{\nu ^{2}}=F\left ( \frac{I_{\nu }}{\nu ^{3}} \right )\)
onde \(F\) é uma função desconhecida. Mas usando a eq. (5), obtemos:
\(\frac{1}{T}=\frac{\partial }{\partial I_{\nu }}\left [ \nu ^{2}F\left ( \frac{I_{\nu }}{\nu^{3}} \right ) \right ]=\frac{1}{\nu}F'\left ( \frac{I_{\nu}}{\nu^{3}} \right )\)
onde a plica designa a derivada da função \(F\) em ordem ao seu argumento. Podemos reescrever este resultado de outra forma:
\(\frac{I_{\nu }}{\nu ^{3}}=f\left ( \frac{\nu }{T} \right )\) (6)
Foi dado um grande passo na solução do problema proposto por Kirchhoff – a intensidade espectral, função da frequência e da temperatura, depende de uma função de uma única variável. O problema ficou consideravelmente simplificado – encontrar a função \(f\left ( x \right )\)! Notar-se-á como a lei de Stefan é reobtida, mesmo sem conhecermos esta função:
\(u=\frac{4\pi}{c}\int_{0}^{\infty }d\nu I_{\nu }=\frac{4\pi}{c}\int_{0}^{\infty }d\nu \nu^{3}f\left ( \frac{\nu}{T} \right )=\frac{4\pi}{c}T^{4}\int_{0}^{\infty }dxx^{3}f\left ( x \right )\) (7)
Assim, a constante de Stefan-Boltzmann é deduzida, se conhecermos este integral. O simples facto do integral ser finito indica-nos que a função \(f\left ( x \right )\) deve anular-se, mais rapidamente que \(\frac{1}{x^{4}}\), para \(x\rightarrow \infty \). Por outro lado, ela também se deve anular para frequência nula \(\left ( \nu =0 \right )\), correspondente a um campo estático e que, portanto, não pode transmitir energia. Assim sendo, a intensidade espectral \(I_{\nu}\), considerada como função da frequência \(\nu\), deve passar por um máximo, e facilmente se conclui que a frequência deste máximo \(\left ( \nu _{m} \right )\) é proporcional à temperatura:
\(\nu_{m}\propto T\)
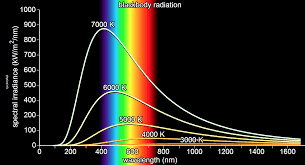
Deste modo, quantomaior for a temperatura, tanto maior é a frequência onde é máxima a intensidade espectral – em linguagem simples, obtemos a cor do objeto quente. Esta relação é conhecida por lei de deslocamento de Wien (justificação do prémio Nobel que recebeu em 1911) e está bem de acordo com a nossa experiência – quando aquecemos um corpo, ele começa a emitir radiação no infravermelho, depois no vermelho, amarelo, azul, ultravioleta... Os sucessivos menores comprimentos de onda traduzem fielmente as sucessivas maiores frequências da radiação dominante (FIGURA 4). Da experiência, obteve-se:
\(\lambda _{m}T=0,2898cmK\) (8)
Assim, à temperatura ambiente \(\left ( T=300K \right )\), a radiação térmica dominante tem comprimento de onda \(\lambda_{m}\approx 96\mu m\), isto é, no infravermelho. Um corpo que assim emitisse parecer-nos-ia bem negro!
Falta determinar a função \(f\left ( x \right )\). Resultados experimentais levaram Wien (1896) a propor:
\(I_{\nu}=\alpha \nu^{3}e^{-\frac{b\nu}{T}}\) (9)
onde \(\alpha\) e \(b\) são constantes ajustáveis. A fórmula parecia funcionar muito bem: medidas efetuadas por Friederich Paschen (1897), no infravermelho próximo \(\lambda =1-8 \mu m\) e numa extensa gama de temperaturas \(\left ( T=400-1600K \right )\), mostraram-se em excelente acordo com a fórmula de Wien. Contudo, em 1900, dois grupos experimentais em Berlim encontram desvios à fórmula de Wien, tanto mais pronunciados quanto maior fosse o comprimento de onda ou maior a temperatura. Curiosamente, os resultados experimentais para essas regiões pareciam aproximar-se bastante bem de uma fórmula desenvolvida por Lord Rayleigh nesse mesmo ano (1900). Vejamos os passos essenciais que conduzem a essa fórmula.
Como vimos, a função \(f\left ( x \right )\), eq. (6), é universal e independente da natureza dos corpos que geram a radiação. E, obtido o equilíbrio térmico, podemos mesmo dispensar os corpos, considerando, apenas, a radiação que enche uma cavidade rodeada por paredes reflectoras. É fácil mostrar que a energia da radiação está associada com as diferentes radiações, independentes umas das outras, cada uma das quais comportando-se como se fosse um oscilador harmónico. Em Junho de 1900, Rayleigh aplicou diretamente a Mecânica Estatística Clássica a este conjunto de osciladores de radiação, obtendo:
\(u_{\nu}=\frac{8\pi}{c^{3}}\nu ^{2}k_{B}T\)
O leitor logo se apercebe que algo está mal – se esta expressão fosse verdadeira, então o integral na eq.(7) diverge! O próprio Lord Rayleigh se apercebeu deste absurdo e sugeriu que a sua fórmula seria uma lei limite, válida se \(\frac{T}{\nu}\) for grande. Mais tarde, no mesmo ano, propôs, sem justificar, a forma:
\(u_{\nu}=\alpha \nu^{2}Te^{-\frac{\beta \nu}{T}}\)
conhecida por fórmula de Rayleigh. Tentou ajustar as constantes, mas cometeu um erro que seria corrigido por James Jeans (1905), passando a chamar-se fórmula de Rayleigh Jeans à primeira expressão de Rayleigh. Esta designação, que o uso consagrou, é um pouco injusta, porque Einstein, em Março de 1905, no seu famoso artigo sobre o efeito fotoeléctrico, reobtém a primeira fórmula de Rayleigh usando um modelo para o oscilador harmónico material, como veremos a seguir. Esse modelo havia já sido considerado por Planck, em 1900, e a importância do trabalho de Einstein consiste em exibir, claramente, que o falhanço da Mecânica Estatística Clássica está não só na sua aplicação aos osciladores de radiação (como fez Rayleigh) mas aos próprios osciladores materiais.

Qualquer modelo suficientemente realista da matéria serve para calcular a função \(f\left ( x \right )\). Em 1897, J. J. Thomson descobre o eletrão e torna-se possível modelizar o átomo, como o fez, logo em 1898, H. Lorentz, obtendo excelentes resultados para a interpretação das propriedades dieléctricas e magnéticas da matéria. O modelo de Lorentz supõe que o eletrão está preso por uma força elástica ao resto do átomo. Imaginemos, então, um oscilador harmónico linear, movendo-se na direção \(x\), sujeito a atrito (para haver absorção de energia – mas não é necessário discutir a natureza deste atrito e podemos, mesmo, considerar a sua grandeza arbitrariamente pequena) e submetido à acção do campo elétrico da radiação[3]:
\(m\ddot{x}+m\gamma x+m\omega _{0}^{2}x=q_{e}E_{x}\left ( t \right )\) (10)
Aqui, \(-m\gamma x\) é a força de atrito e \(m\omega _{0}^{2}\) é a constante elástica, sendo, pois, \(\omega_{0}\) a frequência própria do oscilador. Como referi, esta equação havia já sido utilizado por Lorentz para calcular a suscetibilidade elétrica, e por Planck (1900) que considerou o campo elétrico da radiação. É fácil calcular a resposta do oscilador a um campo elétrico harmónico. Por sobreposição destas soluções, obtemos a resposta para um campo eléctrico arbitrário. Assim, podemos calcular a potência média absorvida, pelo oscilador, do campo de radiação. Se o amortecimento for pequeno, essa absorção é máxima para frequências próximas da ressonância \(\left ( \nu =\frac{\omega _{0}}{2\pi} \right )\), encontrando-se:
\(\left ( \frac{dW}{dt} \right )_{abs}=\left \langle q_{e}E_{x}\left ( t \right )x\left ( t \right ) \right \rangle =\frac{1}{12\epsilon _{0}}\frac{q_{e}^{2}}{m}u_{\nu}\) (11)
Mas se o oscilador tem uma carga \(\left ( q_{e} \right )\), então vai emitir radiação – é, também, relativamente simples, embora demorado, calcular a potência média emitida sob a forma de radiação. Trata-se de radiação dipolar e, sob as hipóteses (que simplificam o cálculo, mas não restringem as conclusões) de fraco amortecimento e pequenas velocidades do oscilador (comparadas com a da luz, no vazio), encontramos:
\(\left ( \frac{dW}{dt} \right )_{em}=\frac{1}{6\pi \epsilon _{0}}\frac{q_{e}^{2}}{m}\omega ^{2}\left \langle E \right \rangle\) (12)
onde \(\left \langle E \right \rangle\) designa o valor médio da energia do oscilador (soma das energias cinética e elástica). No equilíbrio, o oscilador deve absorver, em cada segundo, tanta energia quanto a que emite. Assim, obtemos:
\(u_{\nu}=\frac{8\pi k_{B}}{c^{3}}\nu^{2}T\) (13)
Estes resultados eram, então, bem conhecidos em 1900. Se usássemos a Física Estatística Clássica para calcular o valor médio da energia do oscilador (igual a \(k_{b}T\), onde \(k_{b}\) é a constante de Boltzmann, razão da constante dos gases perfeitos pelo número de Avogadro), encontrávamos a fórmula de Rayleigh-Jeans:
\(u_{\nu}=\frac{8\pi k_{B}}{c^{3}}\nu^{2}T\) (14)
Foi o que fez Einstein, em 1905, para mostrar que algo errado se passava com a Física Estatística Clássica. Ao fazê-lo, reproduziu o resultado de Rayleigh, mas, curiosamente, não foi isto que fez Planck, em 1900, como veremos noutro artigo[4].
O leitor notará que a expressão anterior satisfaz à forma genérica deduzida por Wien. Mas a intensidade espectral assim obtida, para além de originar um valor divergente para a constante de Stefan-Boltzmann, indicava que um corpo radia tanto mais energia quanto maior for a frequência da radiação. Se o leitor abrisse uma fornalha, receberia intensa radiação ultravioleta e ainda mais intensa radiação-X. Algo estava muito errado, passando a designar-se por catástrofe ultravioleta este comportamento absurdo previsto pela Física Clássica.
Referências
- ↑ LAGE, E., A radiação térmica, Rev. Ciência Elem., V8(3):032. (2020). DOI: 10.24927/rce2020.032.
- ↑ LAGE, E., Introdução à Termodinâmica, Rev. Ciência Elem., V7(2):020. (2019). DOI: 10.24927/rce2019.020.
- ↑ LAGE, E., O oscilador harmónico, Rev. Ciência Elem., V7(2):033. (2019). DOI: 10.24927/rce2019.033.
- ↑ LAGE, E., Introdução à Termodinâmica, Rev. Ciência Elem., V7(2):020. (2019). DOI: 10.24927/rce2019.020.
Criada em 10 de Fevereiro de 2020
Revista em 11 de Abril de 2020
Aceite pelo editor em 15 de Junho de 2021

