Força de Lorentz
Referência : Araújo, M., (2015) Força de Lorentz, Rev. Ciência Elem., V3(1):013
Autor: Mariana de Araújo
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2015.013]

A força de Lorentz é a força exercida numa partícula carregada devido à existência de um campo electromagnético. Pode ser considerada como a sobreposição da força devida ao campo eléctrico e da força devida ao campo magnético. Matematicamente, a força de Lorentz é dada pela expressão:
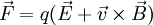 .
.
Índice |
Força Eléctrica
A força exercida por um campo eléctrico numa carga pontual q é proporcional à carga e ao campo na posição ocupada pela carga, e tem a direcção deste:
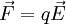
No caso mais simples, o da força entre duas cargas pontuais q1 e q2 em repouso, a força eléctrica entre elas é dada pela força de Coulomb:
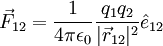 .
.
Em que 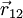 é o vector com origem na carga q1 e extremidade na carga q2, e
é o vector com origem na carga q1 e extremidade na carga q2, e 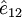 é um vector unitário com a direcção e sentido de
é um vector unitário com a direcção e sentido de 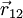 . A constante
. A constante 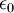 é a permitividade eléctrica do vazio, e tem o valor
é a permitividade eléctrica do vazio, e tem o valor 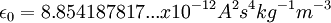 [1].
[1].
Se as cargas tiverem o mesmo sinal, esta força é repulsiva, e se tiverem sinais opostos é atractiva. Note-se que a descrição matemática da força de Coulomb é formalmente semelhante à da força gravítica de Newton. No entanto, a origem do fenómeno electrostático é diferente da do fenómeno gravitacional.
Mais geralmente, o campo eléctrico poderá tomar outra forma, dependendo da distribuição de cargas que cria o campo eléctrico onde a carga q se encontra. Alguns exemplos encontram-se no artigo Campo Eléctrico.
Força Magnética
A força exercida por um campo magnético sobre uma carga pontual q, animada com velocidade 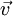 , é proporcional à carga, ao campo magnético, e à velocidade da carga. A direcção da força magnética é perpendicular ao plano definido pelo campo magnético e pela velocidade da carga, e é dada pela expressão:
, é proporcional à carga, ao campo magnético, e à velocidade da carga. A direcção da força magnética é perpendicular ao plano definido pelo campo magnético e pela velocidade da carga, e é dada pela expressão:
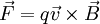 .
.
Uma consequência imediata da força magnética ser perpendicular à velocidade é que esta força não realiza trabalho; contudo, a força magnética altera a direcção da velocidade da partícula. Note-se que, contrariamente à força de Coulomb, a força magnética não é central.
Há duas situações limite de interesse. Uma delas corresponde à situação em que a velocidade da partícula tem a mesma direcção do campo magnético. Nesta situação, a força magnética é nula e, se a partícula estiver livre de outras forças, o seu movimento será rectilíneo e uniforme.
A outra situação corresponde ao caso em que a velocidade da partícula é perpendicular ao campo magnético. Suponhamos, então, a situação em que uma partícula não relativista (v << c), de massa m, carga q e velocidade 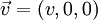 entra numa região onde existe um campo magnético uniforme e estacionário
entra numa região onde existe um campo magnético uniforme e estacionário 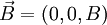 . A força magnética que actua na partícula dá origem a uma aceleração, que se determina através da segunda lei de newton:
. A força magnética que actua na partícula dá origem a uma aceleração, que se determina através da segunda lei de newton:
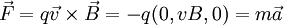
A partícula terá então uma aceleração, cujo valor é 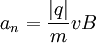 , e direcção sempre perpendicular à velocidade. neste caso, a partícula terá movimento circular e uniforme. O raio da trajectória é dado por:
, e direcção sempre perpendicular à velocidade. neste caso, a partícula terá movimento circular e uniforme. O raio da trajectória é dado por:
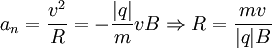
Este raio é chamado o raio ciclotrónico, de Larmor, ou gyroradius. A frequência do movimento, frequência ciclotrónica, é:
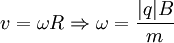
e é independente da velocidade inicial da partícula.
Podemos ver desta análise que:
- Se tivermos uma amostra de partículas todas com a mesma velocidade e carga, e as fizermos passar numa zona onde existe um campo magnético uniforme, o raio da trajectória de cada uma depende unicamente da sua massa. Este facto é a base do funcionamento de um Espectrómetro de Massa.
- É possível determinar a velocidade de uma partícula de massa e carga conhecidas, medindo apenas o raio da trajectória.
- Sabendo a direcção do campo magnético a que a partícula está sujeita, é possível determinar o sinal da sua carga observando a sua trajectória, pois partículas com carga de sinais opostos irão curvar em sentidos opostos.
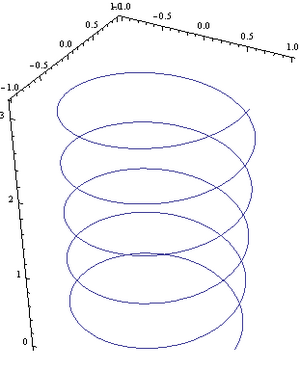
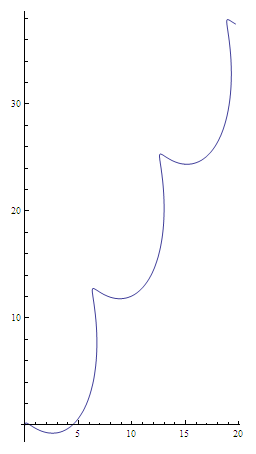
Movimento helicoidal
No caso de a velocidade da partícula ter uma componente paralela e outra perpendicular ao campo, o seu movimento será uma sobreposição de um movimento circular uniforme com um movimento rectilíneo uniforme, e a trajectória resultante é helicoidal, como ilustrado na figura. A componente da velocidade paralela ao campo não é alterada por este, enquanto que a perpendicular ao plano irá sofrer uma força centrípeta que irá curvar a trajectória fazendo a partícula descrever um círculo no plano perpendicular a 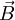 .
.
Sobreposição
Uma carga pontual em movimento numa região do espaço onde estão definidos simultaneamente um campo eléctrico e um campo magnético, fica sujeita à força:
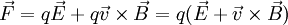 .
.
em situações não-relativistas, a razão entre as intensidades das forças magnética (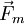 ) e eléctrica (
) e eléctrica ( 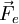 ) é:
) é:
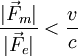 ,
,
em que c é a velocidade da luz no vazio. Assim, para velocidades não-relativistas, temos que o valor da força magnética é inferior ao da força eléctrica. Esta desigualdade não implica que se deva desprezar a força magnética em relação à força eléctrica em qualquer situação (ver exemplos em Ciclotrão e em Espectrómetro de Massa).
Referências
1. 2006 CODATA recommended values, http://physics.nist.gov/cgi-bin/cuu/Value?eqep0%7Csearch_for=permitivity+vaccum
2. Feynman, R., Leighton, R. & Sands, M., The Feynman Lectures on Physics, Vol,. 2, Addison-Wesley Publishing, 1963.
3. Deus, J.D., Pimenta, M., Noronha, A., Peña, T. & Brogueira, P., Introdução à Física, 2ª edição, McGraw-Hill, 2000.
Criada em 05 de Abril de 2011
Revista em 21 de Agosto de 2011
Aceite pelo editor em 21 de Agosto de 2011