Leis da dinâmica de Newton
Referência : Araújo, M., (2013) Leis da dinâmica de Newton, Rev. Ciência Elem., V1(1):014
Autor: Mariana de Araújo
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2013.014]

As leis de Newton são um conjunto de três leis que relacionam as forças exercidas sobre um corpo com o seu movimento, e são suficientes para descrever completamente e de forma determinista a dinâmica de qualquer sistema clássico, conhecidas as forças que sobre ele actuam, e as posições e velocidades de cada partícula num instante 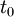 . Foram enunciadas por Sir Isaac Newton no seu livro Philosophiae Naturalis Principia Mathematica em 1687.[1]
. Foram enunciadas por Sir Isaac Newton no seu livro Philosophiae Naturalis Principia Mathematica em 1687.[1]
- Primeira Lei (Lei da inércia): Um corpo em repouso ou em movimento rectilíneo uniforme permanecerá nesse estado, se a resultante das forças que nele actuam for nula.
- Segunda Lei (Lei fundamental da dinâmica): A taxa de variação temporal da quantidade de movimento de um corpo é igual à força resultante nele exercida, e tem a direcção dessa força.
- Terceira Lei (Lei da acção-reacção): Para cada acção existe uma reacção igual e oposta; i.e, as forças resultantes da interacção entre dois corpos são iguais e simétricas, cada uma delas aplicada a um dos corpos.
Os sistemas físicos governados por estas leis são usualmente chamados sistemas clássicos. Estas leis, na sua formulação original, falham no limite quântico, e situações de altas velocidades e de altas energias, em que é necessário aplicar a Mecânica Quântica e Relatividade Geral.
É de notar também que a terceira lei, na formulação aqui apresentada, implica que a perturbação que origina as forças se propagou a uma velocidade infinita. Uma formulação mais geral e correcta não impõe a simetria das forças. No entanto, na generalidade dos casos clássicos (exceptuando a electrodinâmica), esta lei pode ser assim utilizada, uma vez que as velocidades dos corpos envolvidos são muito inferiores à velocidade de propagação da interacção, podendo-se desprezar o intervalo de tempo de propagação e considerar, para todos os efeitos práticos, como instantânea.
Primeira Lei ou lei da inércia
Um corpo em repouso ou em movimento rectilíneo uniforme permanecerá nesse estado, se a resultante das forças que nele actuam for nula.
Esta lei é utilizada na definição de um referencial inercial. Apesar de poder aparentar ser um corolário da segunda lei, na verdade ela define os referenciais em que a segunda lei é válida.
Segunda Lei
A taxa de variação temporal da quantidade de movimento de um corpo é igual à força resultante nele exercida, e tem a direcção dessa força.
Em notação vectorial, sendo que a força resultante a soma vectorial de todas as forças que actuam no corpo:
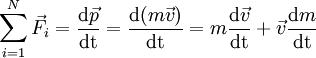
Nos casos em que a massa do corpo não varia, esta lei toma a forma mais conhecida:
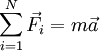
Traduz também a conservação do momento linear do corpo no caso da resultante das forças ser nula:
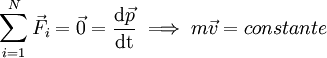
Considere-se agora um sistema formado por N corpos. De um modo geral, estes corpos interactuam entre si e com os corpos exteriores ao sistema. As interacções entre os corpos do sistema satisfazem a terceira lei de Newton, pelo que a sua resultante é nula. Contudo, a resultante das forças com origem na interacção do sistema com a vizinhança, pode não ser nula. A aplicação da segunda lei de Newton ao sistema de N corpos conduz à equação:
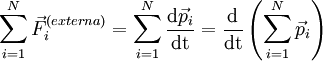
sendo 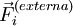 a força resultante das interacções externas sobre o corpo i, e
a força resultante das interacções externas sobre o corpo i, e 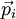 a sua quantidade de movimento. Utilizando a definição de quantidade de movimento do centro de massa, é imediato verificar que:
a sua quantidade de movimento. Utilizando a definição de quantidade de movimento do centro de massa, é imediato verificar que:
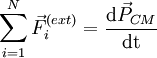 ,
,
isto quer dizer que o movimento global de translação do sistema, sob a acção das forças externas, pode ser descrito pelo movimento do centro de massa. No entanto, podem actuar no corpo forças que, apesar de terem resultante nula, provocam movimento de rotação do corpo, não havendo movimento do seu centro de massa.
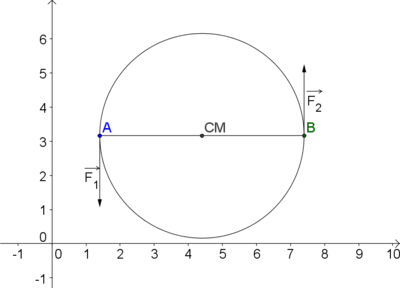
Consideremos o caso simples de um binário de forças, como ilustrado na figura. Os ponto A e B têm a mesma massa, estão rigidamente ligados pelo segmento entre eles, e o sistema está inicialmente em repouso num plano. Se aplicarmos duas forças 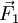 e
e 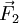 , de igual módulo e sentidos opostos, nos pontos A e B respectivamente, o centro de massa permanecerá fixo, mas os pontos A e B irão descrever um círculo em torno dele.
, de igual módulo e sentidos opostos, nos pontos A e B respectivamente, o centro de massa permanecerá fixo, mas os pontos A e B irão descrever um círculo em torno dele.
Referências
1. Newton, I., Philosophiae Naturalis Principia Mathematica (“Mathematical Principles of Natural Philosophy”), , London, 1687.
2. Halliday, D., Resnick, R., & Walker, J., Fundamentals of Physics, J. Wiley & Sons, 2001.
3. Feymnan, R., Leighton, R. & Sands, M., The Feynman Lectures on Physics, Vol,. 1, Addison-Wesley Publishing, 1963.
4. Alonso, M. & Finn, E., Física, Addison Wesley, 1999.
Criada em 03 de Novembro de 2010
Revista em 06 de Dezembro de 2010
Aceite pelo editor em 06 de Dezembro de 2010