Ciclotrão
Referência : Ferreira, M., (2014) Ciclotrão, Rev. Ciência Elem., V2(4):254
Autor: Miguel Ferreira
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2014.254]

O ciclotrão é um instrumento utilizado para acelerar partículas carregadas até altas energias cinéticas.
O ciclotrão é constituído por dois condutores semi-circulares ocos mantidos no vácuo e dispostos de maneira a formar dois D separados (ver figura 1). Entre estas duas peças aplica-se uma diferença de potencial alternada, cuja frequência é ajustada de modo a que, quando as partículas alcançam a separação entre os dois D, estas sejam aceleradas no mesmo sentido da sua velocidade. Na região dos D 's existe um campo magnético uniforme, independente do tempo, cuja direcção é perpendicular ao plano dos D 's.
Consideremos, por simplicidade, o caso não relativista.
Uma partícula electricamente carregada em movimento, sujeita à acção de um campo magnético uniforme perpendicular à sua velocidade, descreve uma trajectória circular cujo período é independente da velocidade:
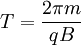 .
.
Os iões produzidos pela fonte, FI, colocada no centro do sistema formado pelos dois D 's, são acelerados pela diferença de potencial entre os D e, ao entrarem num deles, descrevem uma trajectória semi-circular até atingir, ao fim do intervalo de tempo 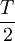 , a separação entre os D.
Entretanto, a diferença de potencial entre os D mudou de sentido e os iões são acelerados, aumentando a sua energia cinética.
No segundo D, o raio da trajectória semicircular é maior do que no primeiro, porque a velocidade da partícula é agora maior do que anteriormente. A partícula volta a alcançar a separação entre os D, passado o intervalo de tempo
, a separação entre os D.
Entretanto, a diferença de potencial entre os D mudou de sentido e os iões são acelerados, aumentando a sua energia cinética.
No segundo D, o raio da trajectória semicircular é maior do que no primeiro, porque a velocidade da partícula é agora maior do que anteriormente. A partícula volta a alcançar a separação entre os D, passado o intervalo de tempo 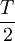 desde a entrada no segundo D. Se a frequência de oscilação do potencial eléctrico for
desde a entrada no segundo D. Se a frequência de oscilação do potencial eléctrico for 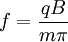 , há uma alternância do sentido da diferença de potencial aceleradora cada
, há uma alternância do sentido da diferença de potencial aceleradora cada 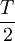 segundos, garantindo que a partícula será acelerada no sentido da sua velocidade, ou seja, havendo sempre um aumento da sua energia cinética, no valor de
segundos, garantindo que a partícula será acelerada no sentido da sua velocidade, ou seja, havendo sempre um aumento da sua energia cinética, no valor de 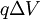 .
.
O processo descrito atrás repete-se várias vezes até que uma placa deflectora desvia a partícula para fora do sistema.
A energia cinética da partícula que sai do ciclotrão está relacionada com o raio máximo que esta descreve antes de sair do sistema:
Sabe-se que o raio de uma partícula de carga 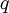 sujeita ao efeito de um campo magnético constante é
sujeita ao efeito de um campo magnético constante é 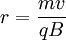 ,
,
então 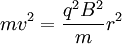 e
e
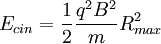 .
.
Aumento relativista da massa
O ciclotrão não pode aumentar indefinidamente a energia de uma partícula carregada. Quando a partícula atinge uma velocidade tal que os efeitos relativistas se tornam apreciáveis, a sua massa efectiva vai aumentar e vai depender da velocidade a que se movimenta. Por essa razão, o tempo que demora a percorrer o a trajectória circular vai deixar de ser independente da sua velocidade:
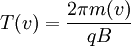
em que 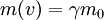
em que 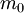 é a massa de repouso da partícula e
é a massa de repouso da partícula e 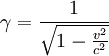 o factor de Lorentz.
o factor de Lorentz.
A sincronização que havia no regime não-relativista entre o movimento da partícula e as oscilações da diferença de potencial deixa de existir. Diz-se que a partícula e a oscilação do potencial estão desfasados. Para terminar, chama-se a atenção de que uma carga acelerada perde energia por radiação.
Ver também
Criada em 21 de Julho de 2011
Revista em 03 de Outubro de 2011
Aceite pelo editor em 03 de Outubro de 2011
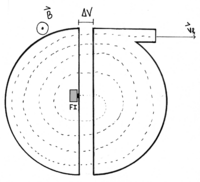
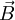 aponta para fora da página,
aponta para fora da página, 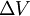 é a diferença de potencial entre as duas peças,
é a diferença de potencial entre as duas peças, 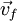 é a velocidade final da partícula e FI representa a fonte de iões que vão descrever trajectórias semi-circulares no ciclotrão.
é a velocidade final da partícula e FI representa a fonte de iões que vão descrever trajectórias semi-circulares no ciclotrão.
