Conjugado de um número complexo
Referência : Ramos, F., (2015) Conjugado de um número complexo, Rev. Ciência Elem., V3(2):123
Autor: Filipe Ramos
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.123]

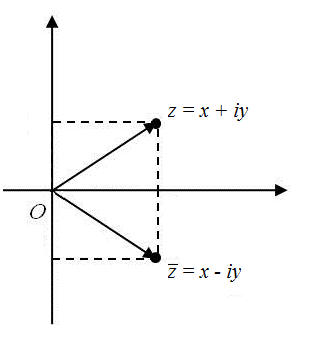
Considerando um número complexo \(z=x+iy\), com \(x,\, y\mathbb{\in R}\),o seu conjugado, escrito na forma algébrica, é o número complexo \(\bar{z}=x-iy\).
Geometricamente:
Nota
- O conjugado de um número complexo cuja parte imaginária é nula (número real) é o próprio número, pois sendo \(z=x\), temos \(\bar{z}=x\).
- O conjugado de um número complexo cuja parte real é nula (imaginário puro), \(z=iy\), é \(\bar{z}=-iy\).
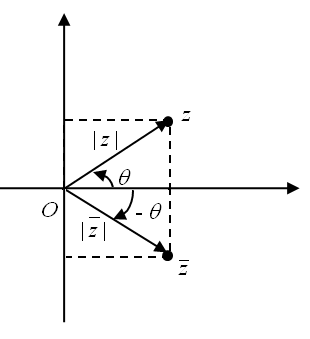
Se \(z\) é um número complexo não nulo e \(\theta = arg(z)\) tem-se, na forma trigonométrica,
\(z =|z|\left(\cos\theta+i\sin\theta\right)\) e \(\bar{z}=|z|\left(\cos\theta-i\sin\theta\right)\).
Como \(|z|=|\bar{z}|\), \(\sin\left(-\theta\right)=-\sin\theta\) (a função seno é ímpar) e \(\cos\left(-\theta\right)=\cos\theta\) (a função cosseno é par), tem-se:
\(\bar{z}=|z|\left(\cos\theta-i\sin\theta\right)\) = \(\bar{z}=|\bar z|\left(\cos( -\theta) +i\sin(-\theta)\right)\),
pelo que \(\left(-\theta\right)\) é um argumento de \(\bar{z}\).
Nota
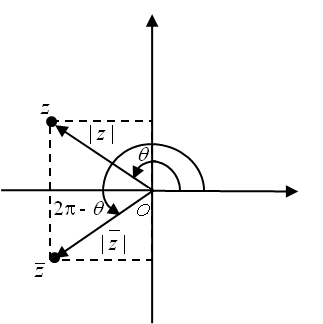
Caso se considere \(\theta\) o argumento positivo mínimo do número complexo \(z\), \(\theta\in\left[0,\,2\pi\right[\), então, o argumento o argumento mínimo de \(\bar{z}\) é \(2\pi-\theta\).
Considerando, por exemplo, \(z\) um número complexo do segundo quadrante, tem-se, geometricamente:
Se um número complexo \(z\), não nulo, está expresso na forma exponencial \(z=|z|\, e^{i\theta}\), onde \(\theta=\arg(z)\), o seu conjugado \(\bar{z}\),na forma exponencial, é \(\bar{z}=|z|\, e^{-i\theta}\).
Em particular, o conjugado do número complexo \(z=e^{ix}\), com \(x\mathbb{\in R}\),
é \(\bar{z}=e^{-ix}\).
Propriedades
Para dois números complexos, \(z\) e \(w\), tem-se:
- \(\overline{z+w}=\overline{z}+\overline{w}\)
- \(\overline{z.w}=\overline{z}.\overline{w}\)
- \(\displaystyle \overline{\left(\frac{z}{w}\right)}=\frac{\overline{z}}{\overline{w}}\) se \(w\neq0\)
- \(\overline{\bar{z}}=z\)
- \(z.\overline{z}=|\, z\,|^{2}\)
- \(|\,\bar{z}\,|=|\, z\,|\)
- \(\displaystyle Re\left(z\right)=\frac{z+\overline{z}}{2}\)
- \(\displaystyle Im\left(z\right)=\frac{z-\overline{z}}{2i}\)
- \(\arg\left(\bar{z}\right)=-\arg\left(z\right)+2k\pi\:,k\in\mathbb{Z}\) se \(z \neq 0\)
Referências
1. Carreira,A. Nápoles,S.(1998) -Variável Complexa: Teoria Elementar e Exercícios Resolvidos.McGraw-Hill, ISBN:972-8298-69-2.
2. Marsden,J.E., Hoffman,J.M. (1998) - Basic Complex Analysis,3ª edição,.W.H. Freeman and Company. ISBN-10: 0-7167-2877-X.
3. Silva,J.S. (1975) - Compêndio de Matemática, 1º Volume (2º TOMO), Gabinete de Estudos e Planeamento do Ministério da Educação e Cultura.
Criada em 22 de Fevereiro de 2012
Revista em 28 de Maio de 2012
Aceite pelo editor em 28 de Maio de 2012