Diferenças entre edições de "Argumento positivo mínimo de um número complexo"
| Linha 4: | Linha 4: | ||
<span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Rodrigue|José Francisco Rodrigues]]</i></span><br> | <span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Rodrigue|José Francisco Rodrigues]]</i></span><br> | ||
<span style="font-size:8pt"><b>DOI</b>: <i>[[http://doi.org/10.24927/rce2014.080 http://doi.org/10.24927/rce2014.080]]</i></span><br> | <span style="font-size:8pt"><b>DOI</b>: <i>[[http://doi.org/10.24927/rce2014.080 http://doi.org/10.24927/rce2014.080]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2014-080.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
---- | ---- | ||
Designa-se por '''argumento positivo mínimo de um número complexo''' \(z\) | Designa-se por '''argumento positivo mínimo de um número complexo''' \(z\) | ||
Edição actual desde as 10h24min de 6 de abril de 2022
Referência : Ramos, F., (2014) Argumento positivo mínimo de um número complexo, Rev. Ciência Elem., V2(4):080
Autor: Filipe Ramos
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2014.080]

Designa-se por argumento positivo mínimo de um número complexo \(z\) (não nulo) o seu argumento que pertence ao intervalo \(\left[0,\,2\pi\right[\).
Exemplo
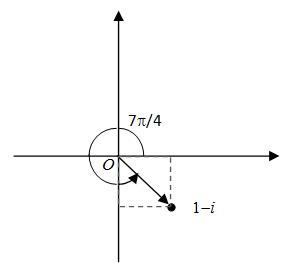
O argumento positivo de \(z=1-i\) é \(\theta=\frac{7\pi}{4}\).
Geometricamente:
Ver
- Argumento de um número complexo
- Argumento principal de um número complexo
- Representação polar (ou trigonométrica) de um número complexo
Referências
1. Carreira,A. Nápoles,S.(1998) -Variável Complexa: Teoria Elementar e Exercícios Resolvidos.McGraw-Hill, ISBN:972-8298-69-2.
2. Marsden,J.E., Hoffman,J.M. (1998) - Basic Complex Analysis,3ª edição,.W.H. Freeman and Company. ISBN-10: 0-7167-2877-X.
3. Silva,J.S. (1975) - Compêndio de Matemática, 1º Volume (2º TOMO), Gabinete de Estudos e Planeamento do Ministério da Educação e Cultura.
Criada em 22 de Fevereiro de 2012
Revista em 28 de Maio de 2012
Aceite pelo editor em 28 de Maio de 2012