Referência : Lage, E., (2023) Teoria da radiação eletromagnética,, Rev. Ciência Elem., V11(3):003
Autores: Eduardo Lage
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2023.003]

---

[editar] Resumo

O azul do céu e o vermelho no ocaso são manifestações da radiação eletromagnética gerada por cargas aceleradas. O campo da radiação deduz-se a partir dos potenciais retardados aqui definidos e obtidas as suas expressões exactas. Para grandes distâncias das fontes e pequenas velocidades das cargas, comparadas com a velocidade da luz, obtém-se uma boa aproximação para o campo de radiação caracterizado por depender da aceleração transversal, em relação à linha de visão do observador. Os resultados são aplicados ao estudo da radiação emitida por um oscilador harmónico e por uma carga em movimento circular, discutindo-se as difusões Thomson e Rayleigh, a instabilidade de modelos clássicos de átomos e a radiação emitida por um magneto em rotação que constitui um modelo aproximado para um pulsar.

As ondas eletromagnéticas são oscilações dos campos elétrico e magnético que se propagam no vazio com a velocidade da luz, sendo detetadas pelas suas interações com cargas e correntes. Inversamente, cargas e correntes que variam no tempo geram ondas eletromagnéticas — são as soluções particulares das equações^[1]:

$\frac{1}{c^2}\frac{\partial^2\varphi }{\partial t^2}-\Delta \varphi=\frac{\rho}{\varepsilon _0}$ (1)

$\frac{1}{c^2}\frac{\partial^2\vec{A} }{\partial t^2}-\Delta \vec{A}=\frac{\vec{i}}{\varepsilon _0c^2}$ (2)

Aqui, $\rho$ e $\vec{i}$ são as densidades de carga e corrente, as fontes do campo, enquanto que $\varphi$ e $\vec{A}$ são os potenciais eletromagnéticos a partir dos quais se deduzem os campos físicos:

$\vec{E}=-\bigtriangledown \varphi-\frac{\partial \vec{A}}{\partial t}$ (3)

$\vec{B}=\bigtriangledown \wedge \vec{A}$ (4)

Se se projetar a equação (2) nos eixos cartesianos, facilmente se percebe que as três equações assim obtidas são analiticamente idênticas à equação (1). Considerar-se-á, então, a solução particular desta equação, adaptando-se imediatamente o resultado final para a solução da equação (2). Considere-se um pequeno volume localizado na origem das coordenadas de modo que a carga instantânea nesse volume é:

$\delta Q(t)=\rho\left ( \vec{0},t \right )dV$ (5)

Será óbvio que a solução da equação (1) para esta carga apresenta simetria esférica. Assim, usando coordenadas esféricas^[2], procura-se soluções da forma:

$\varphi(r,t)=\frac{\psi (r,t)}{r}$ (6)

Considere-se $r\neq 0$, de modo que o segundo membro da equação (1) é nulo para aquela carga. Obtém-se:

$\frac{1}{c^2}\frac{\partial^2\psi} {\partial t^2}-\frac{\partial^2\psi}{\partial r^2}=0\; \; \; \; \; r>0$

A solução genérica desta equação é a sobreposição de duas funções arbitrárias, cada uma só dependente de um único argumento^[3]:

$\psi(r,t)=f(r-ct)+g(r+ct)$ (7)

A função $f$, designada por solução retardada, representa uma onda esférica que se propaga a partir da origem, enquanto a função $g$ (solução avançada) representa uma onda esférica que converge para a origem. Ora, é de esperar que a onda gerada pela carga $\delta Q (t)$ se propague a partir da carga como exige o princípio da causalidade. Assim, será ignorada a solução avançada, o que introduz uma assimetria no tempo que não está presente nas equações de Maxwell.

Regressando à equação (1), com o segundo membro incluído e representando a carga, é evidente que, quando $r\rightarrow 0$, se deve encontrar o potencial eletrostático:

$\varphi(r,t)\xrightarrow[r\rightarrow 0]{}\frac{\delta Q(t)}{4\pi\varepsilon _0r}$

Então, pelas equações (6) e (7), obtém-se:

$f(-ct)=\frac{\delta Q(t)}{4\pi\varepsilon _0}$

Ora, a função $f$ só tem um argumento, $r − ct$. Assim, com o resultado anterior, obtém-se a especificação completa desta função:

$f(r-ct)=\frac{\delta Q\left ( t-\frac{r}{c} \right )}{4\pi\varepsilon _0}=\frac{\rho\left ( \vec{0},t-\frac{r}{c} \right )dV}{4\pi\varepsilon _0}$

Invocando a equação (6), deduz-se o potencial elétrico para esta carga situada, por hipótese, na origem:

$\varphi \left ( \vec{r},t \right )=\frac{\rho\left ( \vec{0},t-\frac{r}{c} \right )dV}{4\pi\varepsilon _0r}$

É, agora, possível generalizar. Primeiro, suponha-se que a posição da carga é $\vec{r}\;'$ e o ponto de observação é $\vec{r}\;'$, de modo que a distância entre a carga e o ponto é $R=\left | \vec{r}\;-\vec{r}\;' \right |$, pelo que a expressão anterior fica:

$\varphi \left ( \vec{r},t \right )=\frac{\rho\left ( \vec{r}\;',t-\frac{R}{c} \right )dV'}{4\pi\varepsilon _0R}$

$\varphi\left ( \vec{r},t \right )=\frac{\rho\left ( \vec{r}\;',t-\frac{R}{c} \right )dV'}{4\pi\varepsilon _0R}$

Segundo, para uma distribuição contínua de cargas, a solução retardada obtém-se por simples aplicação do princípio da sobreposição:

$\varphi\left ( \vec{r},t \right )=\frac{1}{4\pi\varepsilon _0}\int dV'\frac{\rho\left ( \vec{r}\;',t-\frac{R}{c} \right )}{R}$ (8)

Como referido anteriormente, a solução da equação (2) é:

$\vec{A}\left ( \vec{r},t \right )=\frac{1}{4\pi\varepsilon _0c^2}\int dV'\frac{\vec{i}\left ( \vec{r}\;',t-\frac{R}{c} \right )}{R}$ (9)

Estas equações são as soluções exatas para distribuições arbitrárias de cargas e correntes. A partir delas deduzem-se os campos elétrico e magnético através das equações (3) e (4).

Interessa aqui considerar a geração de uma onda eletromagnética dentro de aproximações justificadas. Para isso, começa-se por notar que um raio de luz (FIGURA 1) é a propagação de energia no interior de um cone que subtende um ângulo sólido $d\Omega$ (FIGURA 2): o fluxo de energia, na unidade de tempo, através de qualquer base esférica à distância arbitrária, $r$,do seu vértice é $Ir^2d\Omega$, onde $I$ é a intensidade da radiação, i.e., a grandeza do vetor de Poynting^[4]:

$\vec{S}=\varepsilon _0c^2\vec{E}\wedge \vec{B}$

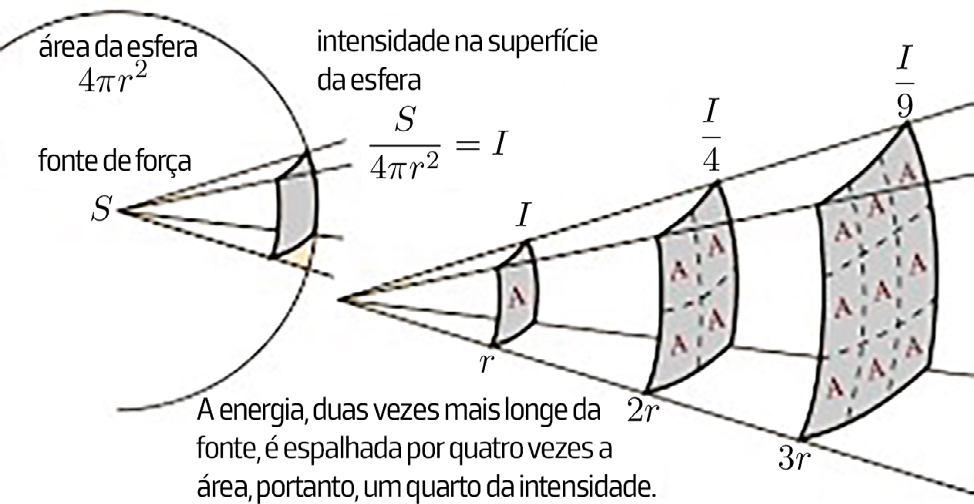
Ora, para uma onda eletromagnética propagando-se no vazio é $B=\frac{E}{c}$, pelo que $I=\left | \vec{S} \right |\propto E^2$. Assim, para um raio de luz, obtém-se $E\propto \frac{1}{r}$. É esta a característica fundamental do campo de radiação que se deve contrastar com o decaimento espacial do campo eletrostático para o qual é $E\propto \frac{1}{r^2}$. Considerando a origem de coordenadas num ponto qualquer no interior da região onde se situam as fontes da radiação, então, numa primeira aproximação, os potenciais ficam, para grandes distâncias dessas fontes:

$\varphi\left ( \vec{r},t \right )\simeq \frac{1}{4\pi \varepsilon _0r}\int dV'\rho\left ( \vec{r}\;',t-\frac{R}{c} \right )$ (11)

$\vec{A}\left ( \vec{r},t \right )\simeq \frac{1}{4\pi \varepsilon _0c^2r}\int dV'\vec{i}\left ( \vec{r}\;',t-\frac{R}{c} \right )$ (12)

O cálculo dos campos elétrico e magnético, equações (3) e (4), obriga a derivar estas expressões em ordem ao tempo e às coordenadas do vetor de posição $\vec{r}$. Ora, em relação a estas, irão ser ignoradas as derivadas do fator $\frac{1}{r}$, porque levam a um decaímento espacial ainda mais rápido dos potenciais. Assim, tais derivadas serão obtidas apenas do tempo retardado:

$t^*=t-\frac{R}{c}$ (13)

Tem-se:

$\bigtriangledown \varphi\simeq \frac{1}{4\pi\varepsilon _0r}\int dV'\frac{\partial \rho\left ( \vec{r}\;',t^* \right )}{\partial t}\left ( -\bigtriangledown \frac{R}{c} \right )$ (14)

Ora, sendo:

$\vec{R}=\vec{r}-\vec{r}\;'$ (15)

então:

$\bigtriangledown R=\frac{\vec{R}}{R}=\vec{e}_R$

onde $\vec{e}_R$ é o versor que aponta das cargas para o ponto de observação. Note-se que qualquer derivada em ordem a uma coordenada deste versor, é de ordem $\frac{1}{r}$ pelo que será ignorada. Reescrevendo a equação (14):

$\bigtriangledown \varphi\simeq -\frac{1}{4\pi\varepsilon _0cr}\int dV'\frac{\partial \rho\left ( \vec{r}\;',t^* \right )}{\partial t}\vec{e}_R$ (16)

Observa-se que a lei de conservação de carga^[5] permite substituir a derivada da densidade de carga:

$\frac{\partial\rho\left ( \vec{r},t \right )}{\partial t}=-\bigtriangledown '\cdot \vec{i}\left ( \vec{r}\;',t \right )$

Aqui, $\bigtriangledown '$ é o gradiente aplicado às componentes de $\vec{r}\;'$. Assim, na equação (16), tem-se:

$\frac{\partial\rho\left ( \vec{r}\;',t^* \right )}{\partial t}=-\left [ \bigtriangledown '\cdot \vec{i}\left ( \vec{r}\;',t' \right )\right ]_{t'=t^*}=-\bigtriangledown '\cdot \vec{i}\left ( \vec{r}\;',t^* \right )+\frac{\partial \vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}\cdot \bigtriangledown 't^*=$

$=-\bigtriangledown '\cdot \vec{i} \left ( \vec{r}\;',t^* \right )+\frac{\partial\vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}\cdot \frac{\vec{e}_R}{c}$ (17)

No segundo membro, o primeiro termo resulta da lei de conservação de carga na qual as derivadas em ordem às coordenadas são efectuadas com tempo fixo, posteriormente calculado no tempo retardado; no segundo termo, a primeira parcela efetua as derivadas espaciais da densidade de corrente incluindo o tempo retardado, corrigindo-se esta expressão na segunda parcela, com as derivadas espaciais do tempo retardado; no último termo, ficam explicitadas estas derivadas notando-se, apenas que $\bigtriangledown 'R=-\bigtriangledown R$. Substituindo na equação (16), tem-se:

$\bigtriangledown \varphi\simeq \frac{1}{4\pi\varepsilon _0cr}\int dV'\left [ \bigtriangledown '\cdot \vec{i}\left ( \vec{r}\;',t^* \right )-\frac{\partial \vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}\cdot\frac{\vec{e}_R}{c} \right ]\vec{e}_R$

No segundo membro, começa-se por incluir o versor $\vec{e}_R$ nas derivadas de $\bigtriangledown '$, subtraindo a ação deste gradiente naquele versor; no primeiro caso, o teorema de Gauss anula o integral e, no segundo caso, obtém-se termos em $\frac{1}{R}$ que se ignoram como atrás se referiu. Assim:

$\bigtriangledown \varphi\simeq \frac{1}{4\pi\varepsilon _0cr}\int dV'\left [ \frac{\partial \vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}\cdot\frac{\vec{e}_R}{c} \right ]\vec{e}_R$ (18)

Está calculada uma das parcelas do campo elétrico na equação (3). Quanto à outra parcela, usando a equação (12), tem-se, simplesmente:

$\frac{\partial \vec{A}\left ( \vec{r},t \right )}{\partial t}\simeq \frac{1}{4\pi\varepsilon _0c^2r}\int dV'\frac{\partial\vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}$

Usando a equação (3), obtém-se finalmente:

$\vec{E}\left ( \vec{r},t \right )=-\frac{1}{4\pi\varepsilon _0c^2r}\int dV'\left [ \frac{\partial\vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}-\left ( \frac{\partial\vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}\cdot \vec{e}_R \right ) \vec{e}_R \right ]=$

$=\frac{1}{4\pi\varepsilon _0c^2r}\int dV'\vec{e}_R\wedge \left ( \vec{e}_R\wedge \frac{\partial \vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t} \right )$ (19)

Quanto ao campo magnético, as equações (4) e (12) dão, nas aproximações referidas:

$\vec{B}\left ( \vec{r},t \right )\simeq \frac{1}{4\pi\varepsilon _0c^2r}\int dV'\bigtriangledown \wedge \vec{i}\left ( \vec{r}\;',t^* \right )=\frac{1}{4\pi\varepsilon _0c^2r}\int dV'\bigtriangledown t^*\wedge \frac{\partial\vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}=$

$=-\frac{1}{4\pi\varepsilon _0c^2r}\int dV'\frac{\vec{e}_R}{c}\wedge \frac{\partial \vec{i}\left ( \vec{r}\;',t^* \right )}{\partial t}$ (20)

Estas expressões serão agora utilizadas para obter uma fórmula aproximada para o campo de radiação originado por uma carga pontual $(q)$ em movimento. Para isso, começa-se por discutir o que é o tempo retardado para tal carga. Considere-se a origem de coordenadas no ponto de observação e designe-se por $\vec{r}\left ( t \right )$ a posição instantânea da partícula. Então, usando a equação (13), o tempo retardado é definido por:

$t^*=t-\frac{\left | \vec{r}\left ( t^* \right ) \right |}{c}$ (21)

Imagine-se uma onda esférica que converge para a origem no instante $t$ (FIGURA 3). A onda atinge antes a carga no instante retardado e a posição desta nesse instante é a sua posição retardada $\vec{r}\left ( t^* \right )$ — tal é o significado da equação (21).

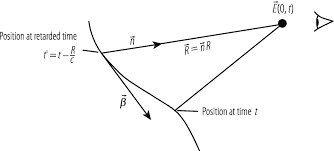
São o instante e posição da carga quando emitiu a radiação que chega ao observador no instante $t$. Quando se olha para o Sol agora, observa-se onde estava cerca de 500 segundos antes. Mas haverá apenas um instante retardado para cada instante t de observação? Se houvesse dois ou mais, haveria duas ou mais imagens da mesma carga a chegarem ao observador naquele mesmo instante $t$, o que só seria possível se a carga tivesse viajado a velocidades superiores à da luz. Do mesmo modo, só poderia não existir instante retardado, i.e., não haver solução da equação (21), se a imaginada onda esférica nunca atingisse a carga, o que manifestamente significa que a carga viaja a velocidades superiores à da luz. Assim, a realização pela experiência comum de cada objecto ter uma e uma só imagem significa que só existe uma solução da equação (21). Da equação (21) deduz-se uma primeira aproximação para o instante retardado, admitindo que a velocidade da carga é muito menor que a velocidade da luz:

$\vec{r}\left ( t^* \right )\simeq \vec{r}\left ( t \right )-\frac{\vec{v}\left ( t \right )}{c}\left | \vec{r}\left ( t^* \right ) \right |\rightarrow \left | \vec{r}\left ( t^* \right ) \right |\simeq \left | \vec{r}\left ( t \right ) \right |-\frac{\vec{r}\left ( t \right )\cdot \vec{v}\left ( t \right )}{c}$ (22)

Assim, para velocidades da carga muito menores que a velocidade da luz, a distância à posição retardada é, praticamente, a distância à posição atual. Como tal, a equação (21) fica:

$t^*=t-\frac{\left | \vec{r}\left ( t\right ) \right |}{c}$ (23)

Doravante, a condição de baixas velocidades $\left ( v\ll c \right )$ será assumida.

Interessa, aqui, considerar o campo eletromagnético gerado por uma carga em movimento em pontos muito afastados da região onde se move a carga. Assim, com uma origem de coordenadas escolhida dentro dessa região, tem-se $R\approx r$, a distância da origem ao observador, e $\vec{e}_R\simeq \vec{e}_r$, o versor que aponta dessa origem para o observador. Nestas condições, as equações (19) e (20) ficam:

$\vec{E}\left ( \vec{r},t \right )=\frac{1}{4\pi\varepsilon _0c^2r}\vec{e}_r\wedge \left [ \vec{e}_r\wedge \int dV'\frac{\partial \vec{i}\left ( \vec{r}\;',t-\frac{r}{c} \right )}{\partial t} \right ]=\frac{1}{4\pi\varepsilon _0c^2r}\vec{e}_r\wedge \left [ \vec{e}_r\wedge \frac{d}{dt}\int dV'\vec{i}\left ( \vec{r}\;',t-\frac{r}{c} \right ) \right ]$

$\vec{B}\left ( \vec{r},t \right )=\frac{1}{4\pi\varepsilon _0c^2}\frac{\vec{e}_r}{c}\wedge \frac{d}{dt}\int dV'\vec{i}\left ( \vec{r}',t-\frac{r}{c} \right )=\frac{\vec{e}_r}{c}\wedge \vec{E}\left ( \vec{r},t \right )$

Para uma corrente de transporte é $\vec{i}=\rho\vec{v}$, de modo que, para uma carga pontual, $q$, tem-se:

$\vec{E}\left ( \vec{r},t \right )\simeq \frac{q}{4\pi\varepsilon _0c^2r}\vec{e}_r\wedge \left [ \vec{e}_r\wedge \vec{a}\left ( t-\frac{r}{c} \right ) \right ]$ (24)

$\vec{B}\left ( \vec{r},t \right )=\frac{\vec{e}_r}{c}\wedge \vec{E}\left ( \vec{r},t \right )$ (25)

onde $\vec{a}$ é a aceleração da carga. O campo elétrico é determinado pela aceleração transversal da carga, i.e., perpendicular à direção definida pela carga e o observador. Tal facto explica o ângulo de Brewster^[6]: na ótica geométrica haveria um raio refletido naquela direção, mas os dipolos que constituem o meio dielétrico estão a vibrar exatamente naquela direção pelo que não há emissão nessa direção e, portanto, não há onda refletida.

Note-se que $\vec{E}$, $\vec{B}$, $\vec{e}_r$ formam um triedro direto. Com estes resultados, obtém-se o fluxo de energia:

$\vec{S}\left ( \vec{r},t \right )=\varepsilon _0c^2\vec{E}\wedge \vec{B}=\varepsilon _0c\left | \vec{E}\left ( \vec{r},t \right ) \right |^2\vec{e}_r$ (26)

Estes resultados são válidos, apenas, dentro das hipóteses referidas (grandes distâncias de observação, cargas com baixas velocidades). A solução exata das equações de campo para uma carga pontual, designadas por equações de Liénard-Wichert, pode ser encontrada na bibliografia, no final deste artigo.

Os exemplos seguintes clarificam estes resultados.

1.º Oscilador harmónico.

A FIGURA 4 representa um oscilador harmónico unidimensional^[7], um modelo simples para a emissão de radiação por dipólos elétricos moleculares. Com o eixo $z$ na direção das oscilações, consideram-se coordenadas esféricas para identificar a posição do observador.

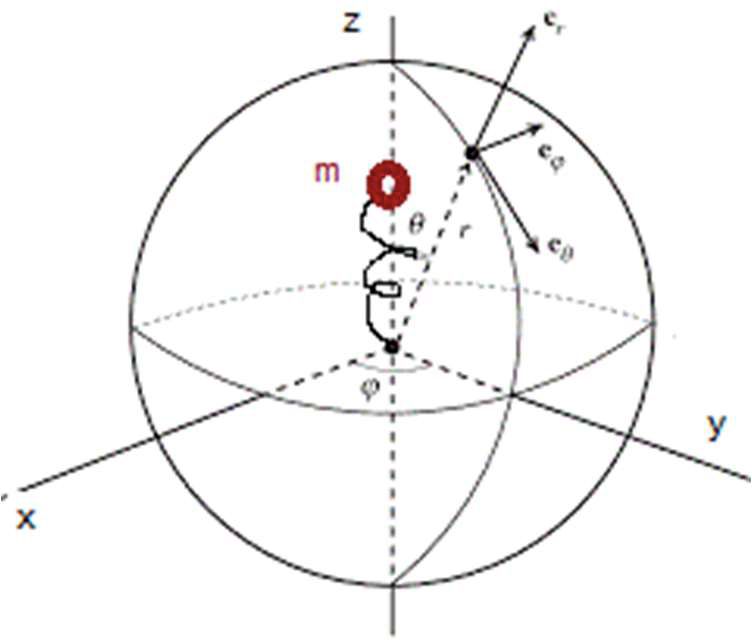
Designando por $\omega _0$ a frequência própria do oscilador, a sua posição em qualquer instante é:

$z=z_0\cos\left ( \omega _0t \right )$

onde $z_0$ é a amplitude da oscilação. Assim, a aceleração transversal para o observador é:

$\vec{a}_T=\omega _{0}^{2}z_0\cos\left ( \omega_0t \right )\sin\theta\vec{e}_\theta$

onde $\vec{e}_\theta$ é o versor dirigido no sentido em que $\theta$ cresce. Usando a equação (24), o campo elétrico da onda radiada é:

$\vec{E}\left ( \vec{r},t \right )\simeq -\frac{q}{4\pi\varepsilon _0c^2r}\vec{a}_T\left ( t-\frac{r}{c} \right )=-\frac{q}{4\pi\varepsilon _0c^2r}\omega_{0}^{2}z_0\sin\theta\textrm{Re}\left [ e^{-i\omega_0\left ( t-\frac{r}{c} \right )} \right ]\vec{e}_\theta$

A onda recebida pelo observador está polarizada linearmente. Para um observador a grandes distâncias do oscilador, a superfície esférica da fase pode ser substituída pelo plano tangente, pelo que o factor de fase se escreve:

$\omega_0\left ( t-\frac{r}{c} \right )=\omega_0t-\vec{k}\cdot\vec{r}$

com $\vec{k}=\frac{\omega_0}{c}\vec{e}_r$ o vetor de onda. Para o observador, trata-se de uma onda plana monocromática como foi já considerada em Ondas eletromagnéticas.

O fluxo de energia da radiação emitida é definido pelo vetor de Poynting, equação (26), obtendo- se para a intensidade (média do fluxo sobre um ciclo de oscilação:

$I\left ( \theta \right )=r^2\left \langle \vec{S}\cdot\vec{e}_r \right \rangle=\varepsilon _0cr^2\left \langle \left | \vec{E} \right |^2 \right \rangle=\frac{\varepsilon _0c}{2}\left ( \frac{q}{4\pi\varepsilon _0c^2}\omega_{0}^{2}z_0\sin\theta \right )^2$ (27)

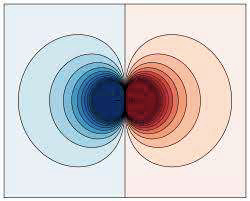
Esta intensidade é designada por dipolar, sendo preponderante no plano perpendicular às oscilações (FIGURA 5). A potência total emitida é:

$\frac{\delta W}{\delta t}=\int d\Omega I\left ( \theta \right )=\frac{q^2}{4\pi\varepsilon _0}\frac{\left ( \omega_{0}^{2}z_0 \right )^2}{3c^3}$

Consequentemente, o oscilador perde energia e vai amortecendo as oscilações. A energia do oscilador é $E_{osc}=\frac{1}{2}m\omega_{0}^{2}z_{0}^{2}$, pelo que:

$\frac{dE_{osc}}{dt}=-\frac{\delta W}{\delta t}\rightarrow \frac{dE_{osc}}{dt}-\gamma E_{osc}$

onde a constante de amortecimento, $\gamma$, é:

$\gamma=\frac{q^2}{4\pi\varepsilon _0}\frac{2\omega_{0}^{2}}{3mc^3}\rightarrow \frac{\gamma}{\omega_0}=\frac{q^2}{4\pi\varepsilon _0\left ( \frac{c}{\omega_0} \right )}\frac{2}{3mc^2}$

A última expressão mostra que a razão $\frac{\gamma}{\omega_0}$ é aproximadamente o quociente da energia potencial elétrica para uma distância da ordem do comprimento de onda $\left ( \lambda=\frac{2\pi c}{\omega_0} \right )$, pela energia em repouso do oscilador. Para a carga de um eletrão e para frequências no visível $\left ( \omega_0\approx 10^{14}s^{-1} \right )$, obtém-se $\frac{\gamma}{\omega_0}\sim 10^{-9}$.

Há um outro importante efeito que o amortecimento, qualquer que seja a sua natureza, introduz na radiação emitida pelo oscilador. Com efeito, a equação de movimento do oscilador dá:

$\frac{d^2z}{dt^2}+\gamma\frac{dz}{dt}+\omega_{0}^{2}z=0$

Procurando soluções da forma $e^{-i\omega t}$, encontram-se duas soluções complexas para $\omega$:

$\omega\pm =-i\frac{\gamma}{2}\pm \sqrt{\omega_{0}^{2}-\left ( \frac{\gamma}{2} \right )^2}$

O movimento genérico do oscilador é, pois, a sobreposição de duas oscilações amortecidas com a mesma frequência (a parte real de $\omega_\pm$). Para simplificar, admita-se que $\gamma\ll \omega_0$; então, a solução da equação de movimento é:

$z\left ( t \right )=z_0e^{-\frac{\gamma t}{2}}\cos\omega_0t$

A diminuição da amplitude processa-se muito lentamente: o oscilador efectua muitas vibrações com a frequência $\omega_0$ antes de diminuir ligeiramente a sua amplitude. Deste modo, pode-se tomar a média do fluxo de energia radiada para um ciclo de vibração, obtendo-se uma intensidade que decai exponencialmente no tempo:

$I\left ( t \right )=I_0e^{-\gamma t}$

onde $I_0$ é a intensidade atrás deduzida. Esta constante de amortecimento, $\gamma$, aparece, também, como a largura da risca espectral de frequência $\omega_0$. Com efeito, a aceleração da carga:

$a(t)=\ddot{z}\simeq -\omega_{0}^{2}z_0e^{-\frac{\gamma t}{2}}\cos\left ( \omega_0t \right )$

não é mais monocromática. Um detetor, por exemplo, rede de difração^[8] é sensível às diferentes frequências na decomposição de Fourier da radiação associada com esta aceleração. Ora:

$\hat{a}(\omega)=\int_{0}^{\infty }dte^{i\omega t}a(t)=\omega_{0}^{2}z_0\frac{i\omega-\frac{\gamma}{2}}{\omega_{0}^{2}-\omega^2-i\gamma\omega}$

A intensidade registada no detetor é proporcional a $\left | \hat{a}(\omega) \right |^2$:

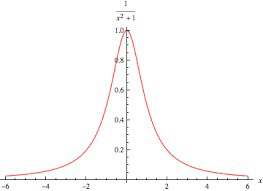
$\left | \hat{a}\left ( \omega \right ) \right |^2\simeq \left ( \omega_{0}^{2}z_0 \right )^2\frac{\omega^2}{\left ( \omega_{0}^{2}-\omega^2 \right )^2+\gamma^2\omega^2}$

A função da frequência no segundo membro, é conhecida por Lorentziana (FIGURA 6). Está concentrada nas vizinhanças da frequência natural do oscilador, apresentando uma largura $\gamma$. É, então, esta a largura da risca de frequência $\omega_0$ observada num espectroscópio.

Imagine-se agora que o oscilador é actuado por uma força externa originada por uma onda eletromagnética que sobre ele incida. A equação de movimento fica:

$\frac{d^2z}{dt^2}+\gamma\frac{dz}{dt}+\omega_{0}^{2}z=\frac{qEa}{m}e^{-i\omega t}$

onde $E_a$ é a amplitude do campo eléctrico da onda incidente. A resposta do oscilador a esta excitação é a solução particular da equação de movimento, apresentado a amplitude complexa:

$z=\frac{qEa}{m}\frac{1}{\omega_{0}^2{-\omega^2}-i\gamma \omega}$

Como consequência da aceleração assim induzida, o oscilador emite radiação dipolar com uma intensidade proporcional à média no tempo da aceleração:

$I\propto \frac{\omega^4}{\left ( \omega_{0}^{2}-\omega^2 \right )^2+\gamma^2\omega^2}$

onde $I_a$ é a intensidade da onda incidente. Reencontra-se a Lorentziana: a intensidade radiada é máxima na ressonância. Na atmosfera, as moléculas comportam-se como osciladores sob acção da luz solar. As frequências próprias destas moléculas (azoto, oxigénio) são muito superiores às frequências na luz visível (essas frequências próprias estão associadas com as energias de fótões que a molécula pode absorver). Nestas condições $\left ( \omega_0\gg \omega \right )$, a intensidade radiada é proporcional à quarta potência da frequência (dispersão Rayleigh, FIGURA 7).

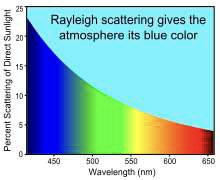
Com o Sol alto, a luz azul é muito mais difundida que a luz vermelha (a frequência do azul é quase 1,6 vezes maior que a do vermelho) — o céu é azul. Mais para Este, a radiação que lá chega já pouco azul ou amarelo contém pelo que o céu no ocaso é avermelhado.

2.º A instabilidade do átomo clássico de hidrogénio.

A FIGURA 8 representa um eletrão (carga $−q$, massa $m$) descrevendo um movimento circular (raio $b$) em torno de um prótão (carga $q$, massa $M\gg m$) praticamente imóvel. Este seria o modelo clássico do átomo de hidrogénio.

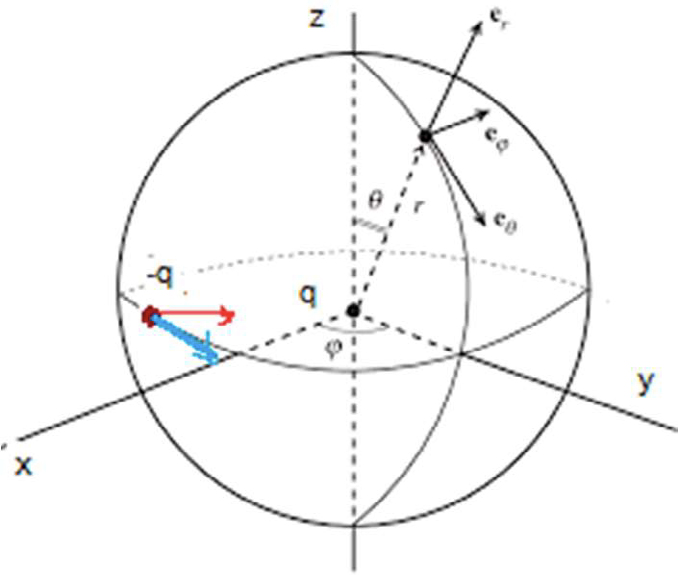
A aceleração do eletrão é centrípeta, $a = \omega^2b$, sendo a frequência angular $\omega$ determinada pela lei fundamental da dinâmica:

$m\omega^2b=\frac{q^2}{4\pi\varepsilon _0b^2}\rightarrow \omega^2b=\frac{q^2}{4\pi\varepsilon _0mb^2}$

O campo eléctrico de radiação gerado pelo eletrão num ponto a grandes distâncias do átomo $\left ( r\gg b \right )$ é:

$\vec{E}\left ( \vec{r},t \right )=\frac{q}{4\pi\varepsilon _0c^2r}\vec{a}_T$

onde $\vec{a}_T$ é a aceleração transversal, i.e., perpendicular ao versor $\vec{e}_r$ das coordenadas esféricas representadas na figura. Facilmente se encontra:

$\vec{a}_T=-\omega^2b\left [ \vec{e}_\theta\cos\theta\cos\left ( \omega t-\phi \right )+\vec{e}_\phi\sin\left ( \omega t-\phi \right ) \right ]$

O vetor de Poynting fica:

$\vec{S}=\varepsilon _0c\left | \vec{E} \right |^2\vec{e}_r=\varepsilon _0c\left ( \frac{q}{4\pi\varepsilon _0c^2r} \right )^2\left ( \omega^2b \right )^2\left [ \left ( \cos\theta\cos\left ( \omega t-\phi \right ) \right )^2+\left ( \sin\left ( \omega t-\phi \right ) \right )^2 \right ]\vec{e}_r$

Efetuando a média para um período de revolução, obtém-se para a intensidade radiada naquela direção:

$I\left ( \theta,\phi \right )=\varepsilon _0c\left ( \frac{q}{4\pi\varepsilon _0c^2} \right )^2 \left ( \omega^2b \right )^2\left ( 1+\left ( \cos\theta \right )^2 \right )$

O fluxo de energia dá-se predominantemente na direção perpendicular ao plano do movimento. Assim, a potência total radiada é:

$\frac{\delta W}{\delta t}=\int d\Omega I\left ( \theta,\phi \right )=\frac{\varepsilon _0c}{2}\left ( \frac{q}{4\pi\varepsilon _0c^2} \right )^2 \left ( \omega^2b \right )^2\frac{8\pi}{3}=\frac{1}{3}\frac{q^2}{4\pi\varepsilon _0c^3}\left ( \omega^2b \right )^2$

Note-se que esta também é, fundamentalmente, a energia radiada num acelerador circular de partículas, embora aí a velocidade das cargas seja próxima da velocidade da luz no vazio. Por tal motivo, esta radiação é designada por sincrotrónica. Com a aceleração da carga atrás deduzida, a potência radiada fica:

$\frac{\delta W}{\delta t}=\frac{c}{3b}\frac{\left ( \frac{q^2}{4\pi\varepsilon _0b} \right )^3}{\left ( mc^2 \right )^2}$

Considere-se $b\simeq 10^{-10}m\left ( 1\dot{\textrm{A}} \right )$ tal como se estima na teoria cinética dos gases. Então, para a carga do eletrão, é $\frac{q^2}{4\pi\varepsilon _0b}\simeq 17\textrm{eV}$, enquanto que $mc^2=5\times 10^5\textrm{eV}$, obtendo-se $\frac{\delta W}{\delta t}\simeq 2\times 10^{10}\textrm{eV/s}$. Ora, sendo $b$ o raio da órbita, a energia do electrão no seu movimento é $\frac{1}{2}m\left ( \omega b \right )^2-\frac{q^2}{4\pi\varepsilon _0b}\simeq -8,5\textrm{eV}$, pelo que em cerca de $10^{-9}s$ o electrão cairia para o núcleo!

Este resultado era do conhecimento de J. J. Thomson quando, em 1897, descobriu o electrão e apresentou o primeiro modelo do átomo: eletrões em repouso numa esfera de prótões. O modelo seria descartado após as experiências de difusão de partículas alfa (núcleos de hélio) por Rutherford, onde se verificou existir um núcleo de raio $10^{5}$ vezes menor que o raio do átomo. Rutherford recupera o modelo planetário do átomo, percebendo-se melhor a enorme audácia de N. Bohr quando, em 1913, postula que o eletrão se situa em órbitas estacionárias onde não radia, só aparecendo radiação quando o eletrão salta de uma dessas órbitas para outra de menor energia, emitindo então um fótão, o quantum da radiação.

3.º A difusão Thomson.

Imagine-se uma onda electromagnética plana e monocromática a incidir sobre uma carga elétrica livre. Escolhendo o eixo $z$ com a direção do vetor de onda incidente, a carga movese no plano perpendicular, oscilando com a frequência da onda incidente e emitindo radiação com a mesma frequência, designada por difusão Thomson (1898). A aceleração é, simplesmente, $\vec{a}=\frac{q}{m}\vec{E}_ae^{-i\omega t}$ (ignora-se o efeito, muito menor, do campo magnético). Usando a geometria da FIGURA 8, encontra-se facilmente a intensidade da radiação emitida:

$I\left ( \theta,\phi \right )=\frac{\varepsilon _cc}{2}\left ( \frac{q^2}{4\pi\varepsilon _0mc^2} \right )^{2}\left [ \left ( \cos\theta \right )^2\left | E_x\cos\phi+E_y\sin\phi \right |^2+\left | E_x\sin\phi+E_y\cos\phi \right |^2 \right ]$

Para radiação incidente não polarizada, obtém-se:

$I\left ( \theta,\phi \right )=\frac{1}{4}\left ( \frac{q^2}{e\pi\varepsilon _0mc^2} \right )^2\left [ \left ( \cos\theta \right )^2+1 \right ]I_{inc}$

onde $I_{inc}$ é a intensidade da radiação incidente. A intensidade total radiada obtém-se por integração sobre o ângulo sólido:

$I=\int d\Omega I=\frac{4}{3}\left ( \frac{q^2}{4\pi\varepsilon _0mc^2} \right )^2I_{inc}=\frac{4\pi}{3}r_{c}^{2}I_{inc}$

onde $r_c$ é o raio clássico do eletrão. Recordar-se-á que $I$ é a potência total difundida enquanto $I_{inc}$ é a potência incidente na unidade de área.

A difusão Thomson é importante no estudo de plasmas ou em Cosmologia onde aparece sobreposta à radiação cósmica de fundo.

4.º Radiação emitia por um magneto em rotação.

Um pulsar é uma estrela de neutrões com a massa do Sol e o raio da Terra. É o que resta da explosão de uma supernova, rodando rapidamente (com períodos do milissegundo) e conservando um fortíssimo campo magnético cujo eixo não coincide com o eixo de rotação. Cargas elétricas, sobretudo eletrões, confinados pelo campo magnético, descrevem órbitas helicoidais em torno do eixo magnético, originando uma fortíssima radiação que atingirá a Terra se o planeta, por acaso, se encontrar na direção do feixe emitido. O movimento das cargas é semelhante ao que ocorre num solenóide gigante, podendo este ser modelizado por um magneto em rotação. Considere-se então a radiação emitida por uma magnetização $\vec{M}$ definindo uma corrente $\vec{i}=\bigtriangledown \wedge \vec{M}$. Substituindo na equação (12), obtém-se:

$\vec{A}\left ( \vec{r},t \right )\simeq \frac{\mu_0}{4\pi r}\int dV'\left ( \bigtriangledown '\wedge \vec{M}\left ( \vec{r}\;',t' \right ) \right )_{t'=t-\frac{R}{c}}$

onde se usou a relação de Maxwell $\varepsilon _0\mu_0c^2=1$.

Procedendo como anteriormente, substitui-se o integrando pela identidade:

$\left ( \bigtriangledown '\wedge \vec{M}\left ( \vec{r}\;',t' \right ) \right )_{t'=t-\frac{R}{c}}=\bigtriangledown '\wedge \vec{M}\left ( \vec{r}\;',t-\frac{R}{c} \right )+\frac{1}{c}\bigtriangledown 'R\wedge \dot{\vec{M}}\left ( \vec{r}\;',t-\frac{R}{c} \right )=$

$=\bigtriangledown '\wedge \dot{\vec{M}}\left ( \vec{r}\;',t-\frac{R}{c} \right )-\frac{\vec{e}_R}{c}\wedge \dot{\vec{M}}\left ( \vec{r}\;',t-\frac{R}{c} \right )$

Aqui, o ponto sobre a magnetização indica derivada em ordem ao tempo. O primeiro termo do último membro, substituído no integral, dá 0, pelo teorema de Gauss. Deste modo, obtém-se:

$\vec{A}\left ( \vec{r},t \right )\simeq -\frac{\mu_0}{4\pi rc}\int dV'\vec{e}_R\wedge \dot{\vec{M}}\left ( \vec{r},t-\frac{R}{c} \right )\simeq -\frac{\mu_0}{4\pi rc}\vec{e}_r\wedge \int dV'\dot{\vec{M}}\left ( \vec{r}\;',t-\frac{r}{c} \right )=$

$=-\frac{\mu_0}{4\pi rc}\vec{e}_r\wedge \dot{\vec{\mu}}\left ( \vec{r}\;',t-\frac{r}{c} \right )$

onde se admitiu grande distância entre o magneto e o observador para se ter $R\simeq r$. Nesta expressão final, $\vec{\mu}$ é o momento magnético do sistema. O campo de radiação é agora facilmente deduzido a partir das equações (3) e (4):

$\vec{E}\left ( \vec{r},t \right )=-\frac{\partial \vec{A}}{\partial t}=\frac{\mu_0}{4\pi rc}\vec{e}_r\wedge \ddot{\vec{\mu}}\left ( \vec{r}\;',t-\frac{r}{c} \right )$

$\vec{B}\left ( \vec{r},t \right )=\bigtriangledown \wedge \vec{A}\simeq -\frac{\mu_0}{4\pi rc}\bigtriangledown \wedge \left [ \vec{e}_r\wedge \dot{\vec{\mu}}\left ( \vec{r}\;',t-\frac{r}{c} \right ) \right ]\simeq$

$\simeq \frac{\mu_0}{4\pi rc^2}\vec{e}_r\wedge \left [ \vec{e}_r\wedge \ddot{\vec{\mu}}\left ( \vec{r}\;',t-\frac{r}{c} \right ) \right ]=\frac{1}{c}\vec{e}_r\wedge \vec{E}$

O magneto roda com a velocidade angular $\vec{\omega}$, pelo que $\dot{\vec{\mu}}=\vec{\omega}\wedge \vec{\mu}$. Escrevendo o momento magnético como soma de uma componente paralela ao eixo de rotação, $\vec{\mu}_{\left | \right |}$, e outra perpendicular àquele eixo, $\vec{\mu}_{\perp }$, é apenas esta que varia no tempo, tendo-se:

$\dot{\vec{\mu}}_\perp =\vec{\omega}\wedge \vec{\mu}_\perp \rightarrow \ddot{\vec{\mu}}_\perp =-\omega^2\vec{\mu}_\perp$

Observe-se que $\left | \vec{\mu}_\perp \right |=\mu\sin\alpha$, onde $\alpha$ é o ângulo entre os eixos de rotação e magnético. O fluxo de energia radiada é obtido através do vetor de Poynting:

$\vec{S}=\vec{E}\wedge \frac{\vec{B}}{\mu_0}=\frac{1}{\mu_0c}\left | \vec{E} \right |^2\vec{e}_r=\frac{\mu_0\omega^4}{\left ( 4\pi c \right )^2c}\left [ \vec{e}_r\wedge \left ( \vec{e}_r\wedge \vec{\mu_\perp }\left ( t-\frac{r}{c} \right ) \right ) \right ]^2\frac{\vec{e}_r}{r^2}$

Note-se a proporcionalidade a $\omega$^[9] tal como na difusão Rayleigh. Para uma observação ao longo do eixo de rotação, a radiação tem polarização circular e para uma observação normal àquele eixo, a radiação apresenta polarização linear. Para outras latitudes, a polarização é elíptica.

A radiação emitida por um pulsar não só informa sobre a sua frequência de rotação como sobre o momento magnético efectivo e o ângulo que este faz com o eixo de rotação. A frequência de rotação é extremamente estável tornando os pulsares em relógios de grande precisão utilizados para navegação de sondas espaciais de longo curso.

Apêndice: Campo electromagnético gerado por carga pontual em movimento arbitrário.

Considere-se a FIGURA 3 onde $\vec{r}(t)$ e $\vec{r}$ designam respetivamente, a posição instantânea da carga e a posição do observador (imóvel), ambas referidas a uma origem de um sistema de eixos cartesianos arbitrário. A posição do observador em relação à carga é notada por $\vec{R}\equiv \vec{r}-\vec{r}(t)$, definindo-se o versor $\vec{e}(t)\equiv \frac{\vec{R}(r)}{R(t)}$. O instante retardado, $t^*$ é determinado pela solução da equação $t^*=t-\frac{R^*}{c}$, onde $R^*=R(t^*)$ é a distância do observador à posição retardada da carga (doravante, o asterisco designa grandezas referidas ao instante retardado). Os potenciais de Liénard-Wichert são as soluções das equações de Maxwell para os potenciais eletromagnéticos gerados pela carga pontual:

$\varphi\left ( \vec{r},t \right )=\frac{q}{4\pi\varepsilon _0R^*}\frac{1}{1-\frac{\vec{v}^*\cdot\vec{e}^*}{c}}$

$\vec{A}\left ( \vec{r},t \right )=\frac{\vec{v}^*}{c^2}\varphi\left ( \vec{r},t \right )$

Aqui, $\vec{v}$ é a velocidade instantânea da carga. O potencial magnético, $\vec{A}$ , é idêntico ao que se obteria para uma carga em movimento uniforme apenas tendo que se referir a velocidade ao instante retardado. O potencial eléctrico é o potencial de Coulomb calculado na posição retardada com uma correcção que o faz aproximar do seu valor na posição actual (veja-se a expressão aproximada para o tempo retardado, equação (22)).

As intensidades dos campos elétrico e magnético deduzem-se destes potenciais usando as equações (3) e (4). O cálculo é bastante extenso não sendo aqui reproduzido, remetendo-se o leitor interessado para a bibliografia sugerida. O resultado final é:

$\frac{4\pi\varepsilon _0}{q}\vec{E}\left ( \vec{r},t \right )=\frac{1}{R^{*2}}\frac{1}{\left ( 1-\frac{\vec{v}^*\cdot \vec{e}^*}{c} \right )^3}\left [ \left ( \vec{e}^*-\frac{\vec{v}^*}{c} \right )\left ( 1-\frac{v^{*2}}{c^2} \right )+\frac{R^*}{c^2}\vec{e}^*\wedge \left ( \left ( \vec{e}^*-\frac{\vec{v}^*}{c} \right )\wedge \vec{a}^* \right ) \right ]$

$\vec{B}\left ( \vec{r},t \right )=\frac{\vec{e}^*}{c^2}\wedge \vec{E}\left ( \vec{r},t \right )$

onde $\vec{a}$ é a aceleração da carga.

O campo elétrico é a soma de um campo de Coulomb, variando como $R^{*^{-2}}$, corrigido por termos que só dependem da velocidade, com o campo de radiação, variando como $R^{*^{-1}}$. Para baixas velocidades da carga, $v\ll c$, o campo de radiação reduz-se à equação (24).

[editar] Referências

1. ↑ LAGE, E., Ondas electromagnética, Rev. Ciência Elem., V9(2):048. (2021). DOI: 10.24927/rce2021.048.
2. ↑ LAGE, E., Gradiente, divergência e rotacional, Rev. Ciência Elem., V8(2):029. (2020). DOI: 10.24927/rce2020.029.
3. ↑ LAGE, E., Campos (Física), Rev. Ciência Elem., V6(2):039. (2018). DOI: 10.24927/rce2018.039.
4. ↑ LAGE, E., Ondas electromagnética, Rev. Ciência Elem., V9(2):048. (2021). DOI: 10.24927/rce2021.048.
5. ↑ LAGE, E., Os fundamentos do Eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
6. ↑ LAGE, E., As equações de Fresnel, Rev. Ciência Elem., V11(1):000. (2023).
7. ↑ LAGE, E., O oscilador harmónico, Rev. Ciência Elem., V7(2):033. (2019). DOI: 10.24927/rce2019.033.
8. ↑ LAGE, E., Ondas, Rev. Ciência Elem., V8(1):016. (2020). DOI: 10.24927/rce2020.016.
9. ↑ LAGE, E., Os fundamentos do Eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.

---

Criada em 26 de Abril de 2022
Revista em 14 de Junho de 2022
Aceite pelo editor em 15 de Março de 2023