Mecânica dos Fluidos
Referência : Lage, E., (2018) Mecânica dos Fluidos, Rev. Ciência Elem., V6(4):084
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2018.084]

Perante a enorme variedade e natureza dos fluidos e o vasto e diverso tipo de comportamentos que apresentam, podíamos ser levados a pensar que não haveria uma descrição universal da sua mecânica. Contudo, não é assim: as leis que regem a dinâmica de qualquer fluido são bem conhecidas e derivam de princípios universais. Sendo assim, onde está a dificuldade em descrevermos quantitativamente o escoamento de um fluido nas suas múltiplas manifestações?
A resposta pode ser já adiantada, embora só mais adiante se perceberá cabalmente a sua essência: as equações básicas são altamente não lineares, um capítulo da matemática ainda por desenvolver completamente. Mesmo a simulação numérica destas equações apresenta, muitas vezes, o fenómeno de caos onde a evolução, para os mesmos dados, da dinâmica de um fluido, embora inteiramente determinista, acaba por originar soluções que divergem exponencialmente ao longo do tempo quer porque a introdução dos dados num computador necessariamente introduz arredondamentos, quer porque as próprias equações têm que ser discretizadas originando uma dependência na “finura” da malha utilizada. É devido ao caos que previsões meteorológicas só são fiáveis para poucos dias, mesmo quando se recorre aos computadores mais avançados. Perante isto, percebe-se que soluções analíticas daquelas equações não são frequentes, mas existem e são de grande importância porque têm um grande domínio de aplicações e porque permitem aferir o grau de fiabilidade de soluções numéricas. Compreende-se, também, que, na prática, aquelas equações fundamentais sejam objeto de aproximações determinadas por números adimensionais (Mach, Taylor, Froude, Prandtl, Rayleigh, Reynolds, etc.), os quais medem a importância relativa de vários termos nas equações, justificando a aproximação utilizada e o âmbito da sua aplicação. Mais abaixo, ver-se-á um exemplo.
Genericamente, um fluido em movimento é descrito por vários campos[1] que mutuamente se influenciam.
a) Em primeiro lugar, temos, evidentemente, o campo (vetorial) de velocidades \({\overrightarrow{\upsilon} \ (\overrightarrow{r},t)}\) ele indica, em cada ponto, a velocidade da pequena porção de fluido aí localizada, em cada instante. Uma linha de corrente é, em cada instante, tangente, em cada ponto, à velocidade naquele ponto e instante; em geral, não coincide com a trajetória de qualquer pequena massa, como se pode observar, com bastante atenção, no movimento de um ribeiro. Só no caso do movimento permanente (i.e. nada depende explicìtamente do tempo) uma linha de corrente coincide com a trajetória das partículas que nela se localizem A partir do campo de velocidades, constrói-se o campo (vetorial) de acelerações \({\overrightarrow{a} \ (\overrightarrow{r},t)}\) - é a aceleração a que está submetida a pequena massa naquele ponto e naquele instante. Esta descrição é conhecida por formulação de Euler mas, apesar da sua simplicidade, esconde uma relação nada trivial entre os dois campos considerados. Com efeito, para obter a aceleração da pequena massa temos de comparar a sua velocidade inicial com a velocidade que tem noutro instante: ora, durante este pequeno intervalo de tempo, a pequena massa deslocou-se da primeira para a segunda posição, isto é:
\(\color{black} {\overrightarrow{a}}\ ({\overrightarrow{r},t})=\frac{1}{\delta t} \left[ {\overrightarrow{\upsilon}} ({\overrightarrow{r}}+{\overrightarrow{\upsilon}} \ \delta t, t + \delta t)- {\overrightarrow{\upsilon}} ({\overrightarrow{r},t})\right]=\frac{\partial {\overrightarrow{\upsilon}}}{\partial t}+{\overrightarrow{\upsilon}}.∇{\overrightarrow{\upsilon}}\equiv\frac{d{\overrightarrow{\upsilon}}}{dt}\)
Introduzimos, aqui, o operador \(\color{black} {\frac{d}{dt}\equiv\frac{\partial }{\partial t}+\overrightarrow{\upsilon}.∇}\) designado por derivada hidrodinâmica: ele determina, para qualquer grandeza, a taxa de evolução temporal dessa grandeza quando acompanhamos uma pequena massa.
b) Em segundo lugar, surge o campo (escalar) da massa específica \(\color{black} {\rho \ (\overrightarrow{r},t)}\), a massa por unidade de volume. Se não existirem reações químicas ou nucleares, a massa de qualquer pequena porção do fluido conserva-se, evidentemente, mas irá, em geral, ocupar diferentes volumes ao longo do tempo e, portanto haverá alterações locais da massa específica. Deixamos, aqui, registada a equação a que tem de obedecer a massa específica, conhecida por equação da continuidade, remetendo para outro lugar a sua dedução:
\(\color{black} {\frac{\partial \rho}{\partial t}}+∇.(\rho\overrightarrow{\upsilon)}=0 \ \ \ \ \ \leftrightarrow \ \ \ \ \ {\frac{\partial \rho}{\partial t}}+\overrightarrow{\upsilon}∇\rho + \rho∇\overrightarrow{\upsilon}\equiv \frac{d\rho}{dt}+\rho∇\overrightarrow{\upsilon}=0\)
Podemos dar uma outra forma a esta equação de maneira a torna-la mais transparente. Designemos por \(υ\) o volume ocupado pela unidade de massa (não confundir o símbolo \(υ\) com o símbolo da velocidade). É óbvio que \(\color{black} \upsilon=\frac{1}{\rho}\). Então:
\(\color{black} {\frac{d\upsilon}{dt}}=-\frac{1}{\rho^2}\frac{d\rho}{dt}=\frac{1}{\rho}∇.\overrightarrow{\upsilon}=\upsilon∇.\overrightarrow{\upsilon}\)
Isto é, a taxa de variação percentual do volume por unidade de massa, \(\color{black} {\frac{1}{\upsilon}\frac{d\upsilon}{dt}}\), é simplesmente determinada pela divergência do campo de velocidades: \(\color{black} {\frac{1}{\upsilon}\frac{d\upsilon}{dt}}=∇.\overrightarrow{\upsilon}\). Então, se pudermos considerar o fluido como incompressível, i.e., a mesma massa ocupa sempre o mesmo volume, o campo de velocidades tem divergência nula, resultado de grande importância em várias aplicações.

c) Em terceiro lugar, temos de considerar os campos de forças que atuam sobre o fluido. Desde logo, o peso que origina a densidade volúmica \(\color{black} {\rho\overrightarrow{g}}\), mas para várias situações, sobretudo em meteorologia ou geofísica, também a força de Coriolis[2] devida à rotação da Terra. O campo de pressões determina outra importante força: se a pequena massa está submetida a uma pressão não uniforme, surgirá uma força que aponta da maior para a menor pressão, i.e., oposta ao gradiente de pressões, originando a densidade volumíca \(\color{black} {-\nabla p}\). Em fluidos viscosos há, também que incluir as tensões viscosas; no caso de fluidos newtonianos[3] e isotrópicos, a tensão é proporcional o gradiente da velocidade, daqui resultando a densidade volumíca[4] \(\color{black} {\eta \Delta \overrightarrow{\upsilon}+\left( \frac{\eta}{3}+ζ \right)∇(∇.\overrightarrow{\upsilon})}\) onde é o coeficiente de \(\eta\) viscosidade dinâmica e ζ é o coeficiente de viscosidade volúmica, ambos, aqui supostos constantes. Note-se que o último termo da expressão anterior, desaparece para fluidos incompressíveis; em qualquer caso, ele será ignorado no que se segue (tal termo, porque proporcional a um gradiente, pode ser adicionado ao termo de pressão, redefinindo, assim, este último campo).
Com estes resultados, a equação fundamental da dinâmica escreve-se:
\(\color{black} {\rho\overrightarrow{a}=\rho\overrightarrow{g}-∇p+\eta \Delta \overrightarrow{\upsilon}}\)
É a equação de Navier-Stokes, a equação fundamental para fluidos viscosos[5]. Ela tem de ser completada com as condições fronteira: perfeita aderência a corpos sólidos (i.e., as velocidades do fluido e do sólido são iguais nos pontos de contacto) ou na superfície que separa dois fluidos viscosos e imiscíveis.
Como aplicação, considere-se o escoamento entre dois planos horizontais, estando fixo o de baixo e movendo-se o de cima com velocidade uniforme [6] (ver FIGURA 1 em “Viscosidade”). O escoamento é suposto permanente e o fluido é considerado incompressível. Tomemos o eixo \(x\) no plano horizontal, alinhado com a direção do movimento do fluido, e o eixo \(y\) na vertical; o terceiro eixo \(z\), normal aos anteriores, não desempenha, aqui qualquer papel. É óbvio que as linhas de corrente são horizontais, coincidindo com as trajetórias das pequenas massas. O campo de velocidades reduz-se à componente \(υ_x\) que não pode depender do tempo (movimento permanente), nem da coordenada \(x\) (fluido incompressível), nem da coordenada \(z\) (por simetria). Assim, \(υx (y)\), apenas. Então, a velocidade de qualquer pequena massa permanece constante ao longo da linha de corrente, i.e., é nula a sua aceleração. Projetando a equação de Navier-Stokes segundo o eixo \(y\), obtemos o campo de pressões que se reduz, afinal, à pressão hidrostática. Projetando segundo o eixo \(x\), obtemos \(\color{black} {\frac{d^2}{dy^2}\upsilon_x=0}\), que se integra facilmente com as condições de aderência aos dois planos: \(\color{black} {\upsilon_x=\frac{U}{h}y}\), onde \(h\) é a distância entre os planos. Assim, o caudal (em volume), por unidade de comprimento transversal (i.e., segundo \(z\)) é \(\color{black} {Q=∫_0^h \ dy\upsilon_x=\frac{Uh}{2} }\). O plano superior exerce a tensão tangencial \(\color{black} {\tau=\eta\left( \frac{d\upsilon_ x}{dy}\right)_ {y=h}=\eta\frac{U}{h} }\), mas move-se uniformemente pelo que a potência das forças que temos de aplicar para manter o seu movimento é \(\color{black} {\eta\frac{U^2}{h} }\) dissipada sob a forma de calor no seio do fluido.
d) O exemplo atrás elaborado mostra que, em fluidos viscosos, deve, também, ser considerado o campo (escalar) da temperatura, o qual se revela responsável por dois efeitos importantes: por um lado, os coeficientes de viscosidade variam fortemente com a temperatura[7] e, portanto, não poderão, em geral, ser considerados constantes; por outro lado, se a temperatura não for uniforme, haverá propagação de calor por condução ou por convexão, surgindo esta última pela dilatação térmica do fluido. Não prosseguiremos aqui estes importantes tópicos, mas a que retornaremos noutras publicações.
e) Por último, temos de analisar o campo de pressões. Cada pequena massa deve ser encarada como um sistema termodinâmico, o que pressupõe ser formada por um número de átomos ou moléculas da ordem do número de Avogadro. Além disso, admitimos que tal pequena massa está em equilíbrio termodinâmico, obedecendo a uma equação de estado que relaciona a pressão, temperatura e massa específica. Por exemplo, para um gás ideal é \(\color{black} {p=\frac{R}{M}\rho T }\), onde \(M\) é a massa molecular, \(R\) a constante dos gases perfeitos e \(T\) a temperatura absoluta. Este equilíbrio é designado por equilíbrio local porque assumido para qualquer pequena massa, embora possa não haver, e geralmente não há, equilíbrio global de todo o fluido como se depreende da existência de um campo de temperaturas, em geral não uniforme.
Os considerandos anteriores servem, essencialmente, para fazer intuír que o escoamento de um fluido apresenta um enorme desafio matemático que só em casos relativamente simples, embora importantes, é suscetível de solução analítica. Um dos principais recursos utilizados em muitas aplicações, consiste em tornar adimensional a equação de Navier-Stokes como, a seguir, ilustraremos com um exemplo simples. Imaginemos um fluido viscoso e incompressível mover-se através de uma configuração geométrica caracterizada por um comprimento \(L\) típico, por exemplo o diâmetro de uma esfera ou de um cilindro imóveis no seio do fluido obrigado, assim, a escoar-se em torno destas figuras. Designemos por \(V\) uma velocidade típica do fluido, por exemplo a velocidade em regiões afastadas daquelas figuras ou determinado pelo caudal. Podemos, agora, mudar para variáveis adimensionais, notadas por uma plica, definidas como segue: \(\color{black} {\overrightarrow{r}'=\frac{\overrightarrow{r}}{L}, t' = \frac{V}{L}t, p'=\frac{p}{\rho V^2},\overrightarrow{g}'=\frac{L\overrightarrow{g}}{V^2} }\). Substituindo na equação, obtém-se:
\(\color{black} {\frac{d\overrightarrow{\upsilon}'}{dt'}=-∇'p'+\frac{1}{Re}\Delta'\upsilon' + \overrightarrow{g}'}\)
onde \(\color{black} {Re=\frac{\rho LV}{\eta}}\) é o número de Reynolds (adimensional). Daqui decorre que, se dois fluidos, em geometrias semelhantes, obedecem a esta mesma equação adimensional, então o comportamento dos dois fluidos é idêntico, apenas tendo que se mudar as escalas. É assim que aviões e automóveis são “experimentados” em túneis de vento, bastando efetuar as experiências com miniaturas geometricamente semelhantes, desde que se garanta que objeto e miniatura estão submetidos ao mesmo número de Reynolds. O ponto mais interessante destas leis de escala é não ser necessário resolver qualquer equação para se conseguir obter respostas adequadas para o sistema de interesse. Por exemplo, a tensão viscosa \(\color{black} {\eta \frac{d\upsilon}{dx}=\frac{\eta V}{L}\frac{d\upsilon'}{dx'}}\) quando integrada sobre a superfície do sólido em contacto com o fluido, origina uma força \(\color{black} {A\eta VL}\), onde \(A\) é um número adimensional que dependerá do número de Reynolds; do mesmo modo, a pressão, integrada sobre a mesma superfície determina uma resultante \(\color{black} {B \rho V^2L^2}\), onde \(B\) é outra constante adimensional que também depende do número de Reynolds. Estas constantes \(A\) e \(B\) podem ser medidas experimentalmente, daqui resultando que a força exercida pelo fluido sobre o sólido tem a forma \(\color{black} {A\eta VL + B \rho V^2L^2}=\eta VL(A+BRe)\).
Voltando à equação anterior, vemos que para grandes números de Reynolds, poderemos, como primeira aproximação, ignorar o termo da viscosidade, simplificando a equação fundamental da dinâmica para a seguinte forma:
\(\rho \overrightarrow{a}=\rho \overrightarrow{g}-∇p\)
Esta é a equação de Euler que rege a mecânica de fluidos perfeitos, i.e., sem viscosidade. Embora de forma aproximada, esta equação descreve um inúmero conjunto de aplicações, como se verá noutras publicações. Aqui, importa realçar que uma solução da equação de Euler como aproximação para um fluido viscoso, falha nas proximidades de corpos sólidos ou nas interfaces entre líquidos. Tal acontece devido às diferentes condições fronteira que fluidos viscosos e perfeitos apresentam naquelas circunstâncias.
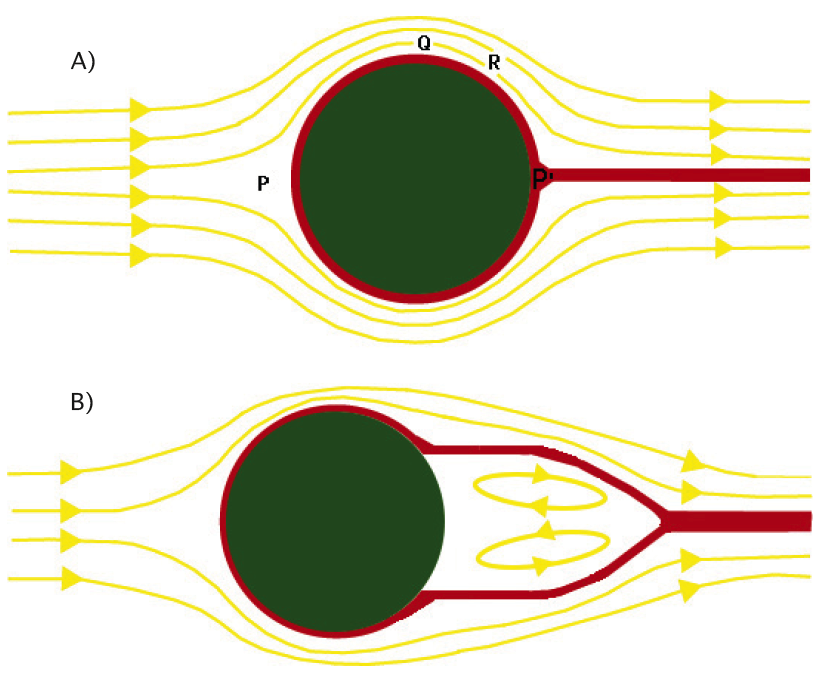
vermelho, separando-se da esfera para maior número de Reynolds, aparecendo, neste caso, vórtices no seu
interior. O fluído é livre de vorticidade fora da camada limite, representada pelo sombreado. Em A) a camada
limite ainda está ligada à esfera, apesar de continuar para além dela. Em B) o fluido separou-se, formando
vortices por trás da esfera.
Um fluido viscoso adere ao sólido enquanto que um fluido perfeito apenas satisfaz a condição de não entrar nem sair do sólido. Deste modo, um fluido viscoso comportar-se-á como perfeito até uma certa distância do corpo sólido ou da interface com outro fluido. Define-se, assim, a camada limite, a região dentro da qual a diferença relativa entre os campos de velocidade de um fluido viscoso e de um fluido perfeito é superior a, por exemplo, 10%. No exterior dessa camada limite, a equação de Euler constituirá uma excelente aproximação da equação de Navier-Stokes.
[editar] Notas
- ↑ Ver “Campos”.
- ↑ Ver “Força”.
- ↑ Ver “Fluidos”.
- ↑ O símbolo Δ representa o laplaciano: \(\color{black} {\Delta = \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+ \frac{\partial ^2}{\partial z^2}}\)
- ↑ A existência e unicidade de solução desta equação para condições gerais, é um dos problemas do Prémio Milénio ainda sem solução.
- ↑ Ver “Viscosidade”.
- ↑ Ver “Viscosidade”.
[editar] Referências
- Massey, B. S., Ward-Smith, A. J., Mechanics of Fluids (9th ed.). London & New York: Spon Press, 2011. ISBN 978-0-415-60259-4. OCLC 690084654
- Tritton, D.J., Physical fluids dynamics. New York: Van Nostrand-Reinhold, 1977.
- J.F. DOUGLAS, J.M. GASIOREK, J.A. SWAFFIELD, Fluid Mechanics, Longman Scientific & Technical, Essex, 1995.
- Lamb, W. Hydrodynamics.
- Lai, W. M. et al., Introduction to continuum mechanics. Butterworth-Heinemann, 2009.
- Prandtl, L., & Tietjens, O. G., Applied Hydrodynamics.
- CURLE, N., DAVIES, H. J., Modern fluid dynamics, 1968.
- Fetter, A. L., & Walecka, J. D., Theoretical mechanics of particles and continua. Courier Corporation, 2003.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 7 de Fevereiro de 2018
Revista em 15 de Fevereiro de 2018
Aceite pelo editor em 4 de Dezembro de 2018

