Massa
Referência : Araújo, M., (2014) Massa, Rev. Ciência Elem., V2(2):154
Autor: Miguel F.
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2014.154]

Em ciência, o termo "massa de um corpo" pode referir-se à sua massa inercial, bem como à sua massa gravitacional, apesar de estar verificado que as duas são equivalentes. Também é comum, no contexto da relatividade restrita, designar por "massa" a massa em repouso do corpo.
A massa inercial (mi) de um corpo é a constante de proporcionalidade entre a força resultante que actua nele e a sua aceleração (excepto se considerarmos um sistema de massa variável). A massa inercial pode ser medida através de um método dinâmico, fazendo colidir frontalmente o corpo com outro em repouso, cuja massa é tomada como unidade. Temos então que:
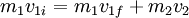 .
.
Medindo as velocidades finais dos dois corpos e conhecida a massa do corpo de referência, podemos calcular a massa inercial do outro.
A massa gravitacional (mg)é a propriedade dos corpos responsável pela interacção gravítica entre eles, tal como a carga é reponsável pela interacção eléctrica e magnética. A massa gravitacional é medida através de um método estático, utilizando uma balança de dois pratos em equilíbrio. Quando os pratos da balança estão equilibrados, a força gravítica exercida pela Terra em cada corpo colocado nos pratos da balança é igual.
A equivalência entre massa inercial e gravitacional foi observada pela primeira vez por Galileo, ao verificar que corpos com massas diferentes em queda livre têm a mesma aceleração. Pela segunda lei de Newton e pela lei da gravitação universal (próximo da superfície da Terra) temos:
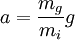
pelo que a aceleração de um corpo em queda livre é sempre igual a g se para todos os corpos 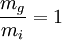 . Esta relação é chamada princípio da equivalência, de grande importância na teoria da relatividade geral. Actualmente a razão entre massa inercial e gravítica está confirmada com uma precisão de 10-13 [1].
. Esta relação é chamada princípio da equivalência, de grande importância na teoria da relatividade geral. Actualmente a razão entre massa inercial e gravítica está confirmada com uma precisão de 10-13 [1].
Referências
1. Adelberger, E.G., “New tests of Einstein’s equivalence principle and Newton’s inverse-square law”, Class. Quantum Grav., 18, 2397–2405, (2001).
Criada em 06 de Setembro de 2010
Revista em 28 de Dezembro de 2010
Aceite pelo editor em 28 de Dezembro de 2010

