Equação de Continuidade de um Fluido em Escoamento
Referência : Ferreira, M., (2014) Equação de Continuidade de um Fluido em Escoamento, Rev. Ciência Elem., V2(4):075
Autor: Miguel Ferreira
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2014.075]

A equação de continuidade é uma consequência da aplicação da conservação da massa no caso do escoamento de um fluido incompressível.
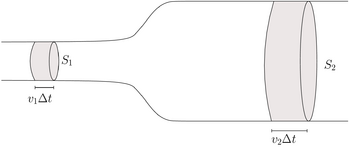
Consideremos que um fluido incompressível (de densidade 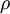 ) se move num tubo rígido, de secção variável. A massa de fluido (
) se move num tubo rígido, de secção variável. A massa de fluido (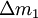 ) que atravessa uma secção recta
) que atravessa uma secção recta 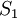 no intervalo de tempo
no intervalo de tempo 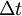 é dada pela expressão:
é dada pela expressão:
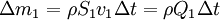 ,
,
em que 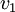 é a componente da velocidade do fluido que é perpendicular à secção recta
é a componente da velocidade do fluido que é perpendicular à secção recta 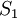 . Reparemos que
. Reparemos que 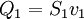 é o caudal volumétrico.
é o caudal volumétrico.
No mesmo intervalo de tempo, a quantidade de massa (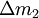 ) que atravessa outra secção recta
) que atravessa outra secção recta 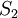 do tubo é:
do tubo é:
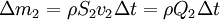 ,
,
com 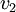 a representar a componente da velocidade de fluido perpendicular a
a representar a componente da velocidade de fluido perpendicular a 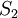 . reparemos que
. reparemos que 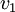 e
e 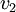 têm o mesmo sentido.
têm o mesmo sentido.
Admitindo que não há fontes nem sorvedouros de fluido no tubo e lembrando que o fluido é incompressível, toda a massa que atravessa a secção 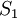 num dado intervalo de tempo vai ter que atravessar, no mesmo intervalo de tempo, a secção
num dado intervalo de tempo vai ter que atravessar, no mesmo intervalo de tempo, a secção 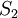 , pelo que:
, pelo que:
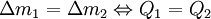 .
.
A última expressão constitui a formulação matemática da equação de continuidade.
Como 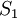 e
e 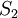 são duas secção rectas arbitrárias, conclui-se que o caudal, medido em qualquer secção de um tubo num dado intervalo de tempo, é constante.
são duas secção rectas arbitrárias, conclui-se que o caudal, medido em qualquer secção de um tubo num dado intervalo de tempo, é constante.
Ver também
Criada em 07 de Agosto de 2011
Revista em 27 de Novembro de 2011
Aceite pelo editor em 27 de Novembro de 2011
 .
.
