Pi
Referência : Tavares, JN, Geraldo, A (2017) Pi, Rev. Ciência Elem., V5(01):004
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Francisco Rodrigues
DOI: doi.org/10.24927/rce2017.004

Resumo
O número \(\pi\) define-se através de
\(\pi=\displaystyle \frac{\mbox{perímetro de uma circunferência}}{\mbox{diâmetro dessa circunferência}}\)
A definição anterior tem uma dificuldade - como se define o perímetro de uma circunferência?
No seu livro "Medição de um círculo", Arquimedes mostrou que \(\pi\)
tem um valor situado entre \(3\displaystyle \frac{10}{71}\) e
\(3\displaystyle \frac{10}{70}\). A ideia é encaixar a circunferência
entre polígonos regulares, respetivamente inscritos e
circunscritos, com um número de lados cada vez maior.
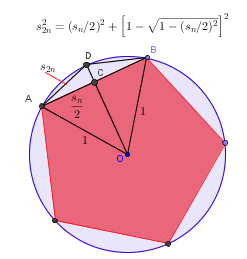
A figura 1 mostra uma circunferência de raio 1, e um polígono regular inscrito com n lados (na figura n=5). \(s_n=AB =\) comprimento de um lado desse polígono. D bisseta o arco AB e portanto \(s_{2n}=AD=DB\) = comprimento de um lado de um polígono regular inscrito com 2n lados.
Aplicando o teorema de Pitágoras ao triângulo ACD, retângulo em C, obtemos
\(s_{2n}^2=AD^2=AC^2+CD^2=AC^2+(OD-OC)^2=\left(\displaystyle \frac{s_n}{2}\right)^2+(1-OC)^2\)
Uma segunda aplicação do teorema de Pitágoras, desta vez ao triângulo ACO, retângulo em C, dá
\(OC=\sqrt{OA^2-AC^2}= \sqrt{1- \left(\displaystyle \frac{s_n}{2}\right)^2}\)
Substituindo na primeira equação e fazendo alguns cálculos simples obtemos então (verifique)
\(s_{2n}=\sqrt{2-\sqrt{4-s_n^2}}\)
o que nos permite calcular \(s_{2n}\) à custa de \(s_n\).
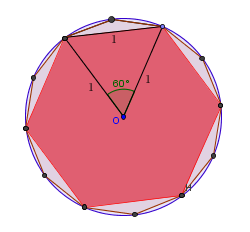
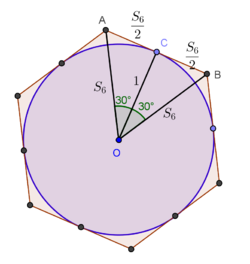
Se agora fizermos n=6 (um hexágono regular inscrito), sabemos que \(s_6=1\) (figura 2). Aplicando sucessivamente a fórmula anterior, e após alguns cálculos simples, vem que\(\begin{eqnarray*} s_{12} &=& \sqrt{2-\sqrt{3}}\nonumber\\ s_{24} &=& \sqrt{2-\sqrt{2+\sqrt{3}}}\nonumber\\ s_{48} &=& \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\nonumber\\ s_{96} &=& \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\nonumber \end{eqnarray*}\)
e assim sucessivamente.
O perímetro de um polígono regular de 96 lados, inscrito numa circunferência de raio 1, é pois igual a \(\displaystyle 96\times s_{96}\) o que dá uma boa aproximação do perímetro dessa circunferência. Como
\(\pi=\displaystyle \frac{\mbox{perímetro de uma circunferência}}{\mbox{diâmetro dessa circunferência}}\),
obtemos a seguinte aproximação de \(\pi\)
\(\pi\approx 48 \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}\approx 3.14103 \approx 3\displaystyle \frac{10}{71}\)
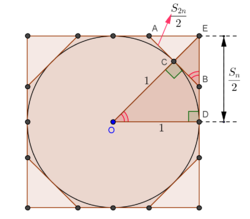
\(S_{2n}=\displaystyle \frac{2\sqrt{4+S_n^2}-4}{S_n} \ \ \ \ \ \ \ \ (*)\)
\(\pi\approx 3.14271\approx \displaystyle3\frac{1}{7}\)
Referências
C.H. Edwards, Jr., The Historical Development of the Calculus, Springer-Verlag, New York, 1979.
T.L. Heath, The Works of Archimedes. Cambridge University Press, 1897 (Dover reprint).
Criada em 12 de Novembro de 2012
Revista em 15 de Março de 2017
Aceite pelo editor em 15 de Março de 2017