Diferencial
Referência : Tavares, J. N., (2018) Diferencial, Rev. Ciência Elem., V6(1):088
Autor: João Nuno Tavares
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2018.088]

Dada uma função 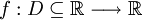 , suponha que existe a derivada de f num ponto a, interior ao domínio de f.
Considere os pontos
, suponha que existe a derivada de f num ponto a, interior ao domínio de f.
Considere os pontos 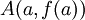 e
e 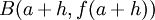 , com
, com 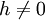 , ambos sobre o gráfico de f, e a recta que os une.
, ambos sobre o gráfico de f, e a recta que os une.
Qual a equação cartesiana desta recta?
Como se sabe da geometria analítica plana, a equação da recta que une os pontos A e B é:
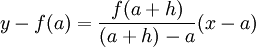
ou:
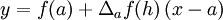
Portanto o declive desta recta, isto é, a tangente do ângulo positivo que esta recta faz com a parte positiva do eixo dos xx, é igual à taxa média de variação de f em a.
Qual a posição limite desta recta quando 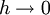 ?
?
Quando 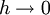 a taxa média de variação de f em a,
a taxa média de variação de f em a, 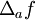 , converge para a taxa instantânea de variação de f em a, isto é, converge para a derivada f'(a) de f em a (supondo que esta existe).
, converge para a taxa instantânea de variação de f em a, isto é, converge para a derivada f'(a) de f em a (supondo que esta existe).
Portanto a recta que une A e B tem uma posição limite que não é mais do que a recta tangente ao gráfico de f no ponto 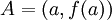 . A respectiva
equação é obtida a partir da equação anterior em , fazendo
. A respectiva
equação é obtida a partir da equação anterior em , fazendo 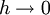 :
:
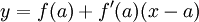
O declive da recta tangente ao gráfico de f no ponto 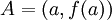 , é pois igual à derivada
, é pois igual à derivada 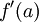 de f em a.
de f em a.
Considere ainda os pontos seguintes:
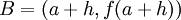 , no gráfico de f e
, no gráfico de f e 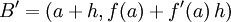 , na recta tangente ao gráfico de f no ponto
, na recta tangente ao gráfico de f no ponto 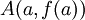
A diferença das ordenadas destes dois pontos é igual a:
![\displaystyle f(a+h)- [f(a)+f'(a)\,h]](/wiki/images/math/0/3/2/032c9e8f080af6e585263cdbc8a5d129.png) e esta diferença é cada vez mais pequena quanto mais próximo de 0 estiver o "acréscimo" h. Neste sentido podemos pois dizer que o valor exacto
e esta diferença é cada vez mais pequena quanto mais próximo de 0 estiver o "acréscimo" h. Neste sentido podemos pois dizer que o valor exacto 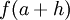 é aproximadamente igual a
é aproximadamente igual a 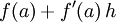 , sendo esta aproximação cada vez mais precisa quanto mais pequeno é o valor de h:
, sendo esta aproximação cada vez mais precisa quanto mais pequeno é o valor de h:
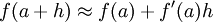
Mais concretamente: se definirmos o erro 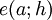 através da diferença:
através da diferença:
![\displaystyle e(a;h) \doteq f(a+h)- [f(a)+ f'(a)h ]](/wiki/images/math/6/4/9/649bed1bb43d26551376b199a72b9ad4.png) podemos dizer que:
podemos dizer que:
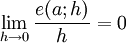 Diz-se então que o erro
Diz-se então que o erro 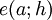 é um infinitésimo de ordem superior a h.
é um infinitésimo de ordem superior a h.
A diferencial da função f no ponto a, é a função 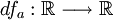 que a cada acréscimo
que a cada acréscimo 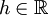 associa o valor
associa o valor
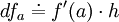 . É pois uma função linear em
. É pois uma função linear em 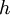 - de facto a função linear que melhor aproxima f em a, no sentido em que:
- de facto a função linear que melhor aproxima f em a, no sentido em que:
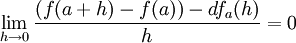
que não é mais do que a versão formal do que se disse antes, e que se presta a generalização.
Criada em 25 de Novembro de 2009
Revista em 14 de Janeiro de 2010
Aceite pelo editor em 31 de Março de 2018

