Fórmulas da soma e da diferença de dois ângulos

Referência : Tavares, J., Geraldo, A., (2017) Fórmulas da soma e da diferenaça de dois ângulos, Rev. Ciência Elem., V5(3):076
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.076]

---

Adição de dois ângulos

Figura 1

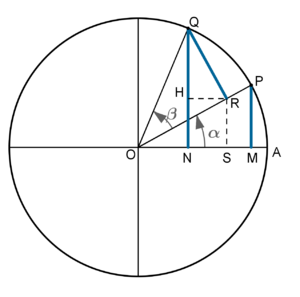
Consideremos um círculo trigonométrico e sejam \(\alpha\) e \(\beta\) dois ângulos positivos de vértice no centro \(O\) do círculo. Por simplicidade vamos considerar o caso em que a soma \(\alpha+\beta\) é menor do que \(\displaystyle \frac{\pi}{2} \mbox{ rad}\). Os outros casos tratam-se de forma análoga, recorrendo a relações trigonométricas.

Os lados extremidades dos ângulos \(\alpha\) e \(\beta\) intersectam a circunferência em dois pontos, denominados \(P\) e \(Q\), respetivamente. Por esses dois pontos, traçamos dois segmentos de reta perpendiculares a \(OA\), \([PM]\) e \([QN]\), respectivamente (Fig.1). Por \(Q\) tracemos um segmento de reta \([QR]\) perpendicular a \(OP\) e por \(R\) tracemos um segmento de reta \([HR]\) paralelo a \(OA\) e um segmento de reta \([RS]\) perpendicular a \(OA\) (ver figura 1).

Obtemos assim três triângulos retângulos \([OPM]\), \([ORS]\) e \([HQR]\) que são semelhantes.

Como se trata de um círculo cujo raio tem uma unidade, as definições de seno e cosseno de um ângulo agudo permitem-nos estabelecer as seguintes relações:

\(\sin \alpha= \overline{PM}\)  ; \(\cos \alpha= \overline{OM}\)  ; \(\sin \beta= \overline{QR}\)  ; \(\cos \beta= \overline{OR}\)

\(\sin (\alpha+\beta)\)\(= \overline{QN}=\overline{QH}+\overline{RS}\)  ; \(\cos (\alpha+\beta)\)\(= \overline{ON}=\overline{OS}-\overline{HR}\)

O facto de \([ORS]\) e \([OPM]\) serem triângulos semelhantes permite estabelecer a seguinte igualdade \(\displaystyle \frac {\overline{RS}}{\overline{PM}}=\frac{\overline{OS}}{\overline{OM}}=\frac{\overline{OR}}{\overline{OP}}\) que, atendendo as relações estabelecidas anteriormente é equivalente a \(\displaystyle \frac {\overline{RS}}{\sin \alpha}=\frac{\overline{OS}}{\cos \alpha}=\frac{\cos \beta}{1}\). Daqui resulta que, \(\overline{RS}\) \(=\sin \alpha \, \cos \beta\) e \(\overline{OS}\) \(=\cos \alpha \, \cos \beta\).

Atendendo ao facto de \([HQR]\) e \([OPM]\) também serem triângulos semelhantes podemos da mesma forma estabelecer a seguinte igualdade \(\displaystyle \frac {\overline{HR}}{\overline{PM}}=\frac{\overline{QH}}{\overline{OM}}=\frac{\overline{QR}}{\overline{OP}}\) que, usando as relações estabelecidas anteriormente para o seno e cosseno dos ângulos é equivalente a \(\displaystyle \frac {\overline{HR}}{\sin \alpha}=\frac{\overline{QH}}{\cos \alpha}=\frac{\sin \beta}{1}\). Daqui resulta que, \(\overline{HR}\)\(=\sin \alpha \, \sin \beta\) e \(\overline{QH}\)\(=\cos \alpha \, \sin \beta\).

Deduzimos então, das igualdades e relações estabelecidas anteriormente, que:

\[\quad \sin (\alpha +\beta)=\sin \alpha \, \cos \beta + \sin \beta \, \cos \alpha \quad\]		\[\quad \cos (\alpha +\beta)=\cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta \quad\]

Sabemos ainda que, para todo o ângulo \(\alpha +\beta\) com \(\cos (\alpha+\beta) \neq 0\) se tem \(\displaystyle \tan (\alpha+\beta)=\frac{\sin (\alpha+\beta)}{\cos (\alpha+\beta}\).

Dividindo ambos os termos da fração por \(\cos \alpha \, \cos \beta\) (\(\cos \alpha \neq 0\) e \(\cos \beta \neq 0\)) a igualdade anterior é equivalente a:

\[\quad \displaystyle \tan (\alpha+\beta)=\frac{\tan \alpha +\tan \beta}{1-\tan \alpha \, \tan \beta} \quad\]

Uma outra prova da fórmula do seno da soma

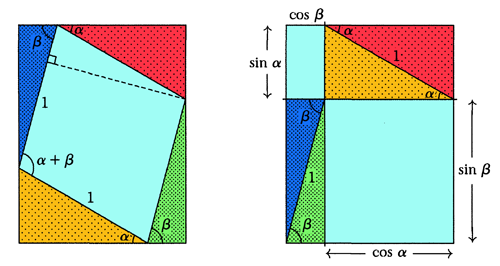
A demostração seguinte deve-se a Volker Priebe e Edgar A. Ramos ``Proof without Words: The Sine of a Sum"; Mathematics Magazine, Vol. 73, No. 5 (Dec., 2000), p. 392. A figura fala por si:

Mas eis algumas indicações:

1. os dois rectângulos têm a mesma largura e o mesmo comprimento (e portanto a mesma área). Porquê?
2. o quadrilátero azul claro contido no rectângulo da esquerda é um paralelogramo. Porquê? A área desse paralelogramo é igual a \(\sin(\alpha+\beta)\). Porquê?
3. A área do paralelogramo azul claro contido no rectângulo da esquerda é igual à soma das áreas dos dois rectângulos azul claro contidos no rectângulo da direita. Porquê? A soma destas áreas é pois \(\sin\alpha \cos \beta + \cos\alpha \sin \beta\). Porquê?
4. Portanto:

\(\sin(\alpha+\beta)= \sin\alpha \cos \beta + \cos\beta \sin \alpha \)

Subtração de dois ângulos

O problema da subtração de dois ângulos pode ser reduzido ao anterior se considerarmos a diferença \(\alpha -\beta\) como a soma do ângulo \(\alpha\) com o ângulo \(-\beta\), ou seja,

\(\sin (\alpha - \beta)=\sin \, [\alpha + (-\beta)]\, = \sin \alpha \, \cos(-\beta)+\sin (-\beta) \, \cos \alpha\quad\) como \(\quad\cos (-\beta)=\cos(\beta)\) e \(\sin (-\beta)=-\sin \beta\) temos então que:

\[\quad \sin (\alpha - \beta)=\sin \alpha \, \cos \beta - \sin \beta \, \cos \alpha \quad\]

Da mesma forma, temos que \(\cos (\alpha - \beta)=\cos \, [\alpha + (-\beta)]\, = \cos \alpha \, \cos(-\beta)-\sin \alpha \, \sin (-\beta)\) é então equivalente a:

\[\quad \cos (\alpha - \beta)=\cos \alpha \, \cos \beta + \sin \alpha \, \sin \beta \quad\]

Sabemos ainda que, para todo o ângulo \(\alpha -\beta\) com \(\cos (\alpha-\beta) \neq 0\) se tem \(\displaystyle \tan (\alpha-\beta)=\frac{\sin (\alpha-\beta)}{\cos (\alpha-\beta}\).

Dividindo ambos os termos da fração por \(\cos \alpha \, \cos \beta\) (\(\cos \alpha \neq 0\) e \(\cos \beta \neq 0\)) a igualdade anterior é equivalente a:

\[\quad \displaystyle \tan (\alpha-\beta)=\frac{\tan \alpha -\tan \beta}{1+\tan \alpha \, \tan \beta} \quad\]

Referências

1. J. Jorge G. Calado (1974) "Compêndio de Trigonometria" 4ªedição. Liv. Popular de Francisco Franco, Lisboa.

---

Criada em 15 de Janeiro de 2013
Revista em 30 de Março de 2013
Aceite pelo editor em 30 de Setembro de 2017