Diagrama de Venn
Referência : Martins, E.G.M., (2014) Diagrama de Venn, Rev. Ciência Elem., V2(1):020
Autores: Maria Eugénia Graça Martins
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2014.020]

Dá-se o nome de diagrama de Venn a todo o diagrama que possibilita a visualização de propriedades e de relações entre um número finito de conjuntos.
Os diagramas de Venn são representados por linhas fechadas, desenhadas sobre um plano, de forma a representar os conjuntos e as diferentes relações existentes entre conjuntos e elementos.
Exemplo:
Considerando o conjunto dos números naturais \(\mathbb{N}=\{1,2,3,4,\cdots\}\), sejam U o conjunto dos números naturais até 25 e \(\rm A\) e \(\rm B\), respetivamente, os conjuntos dos números primos até 25 e números pares até 25:
\[\rm{A}=\{2,3,5,7,11,13,17,19,23\}, \, \rm{B}=\{2,4,6,8,10,12,14,16,18,20,22,24\}\] Recorrendo à utilização de Diagramas de Venn podemos visualizar os conjuntos anteriores, assim como as seguintes operações:
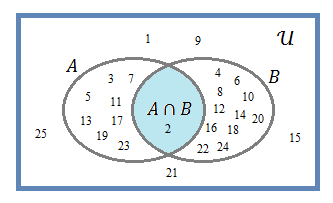
- Interseção entre A e B
\(\quad \rm{A}\cap\rm{B}=\{2\}\)
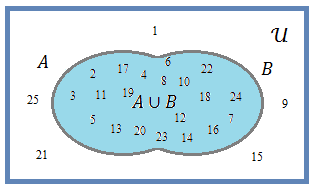
- Reunião entre A e B
\(\quad \rm{A}\cup\rm{B}=\{2,3,4,5,6,7,8,10,11,12,13,14,16,17,18,19,20,22,23,24\}\)
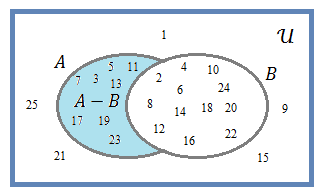
- Diferença entre A e B ou complementar relativo de A em B (A\B ou A-B)
\(\quad \rm{A}-\rm{B}=\{3,5,7,11,13,17,19,23\}\)
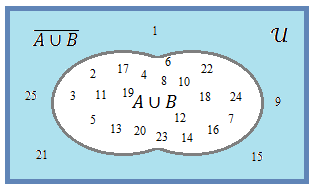
- Complementar da reunião entre A e B
\(\quad \overline{\rm{A\cup B}}:=\)U\(- \left(\rm{A}\cup\rm{B}\right) = \{1,9,15,21,25\}\)
Observação:
Dado um conjunto \(\rm{M}\) o seu conjunto complementar pode ser designado simbolicamente por \(\rm{\bar{M}}\), \(\rm{M^C}\) e C\(\rm{M}\).
Em Estatística utilizam-se diagramas de Venn para visualizar o espaço de resultados e os acontecimentos associados a um fenómeno aleatório. Para representar o espaço de resultados S utiliza-se um retângulo e no seu interior regiões fechadas para representar os acontecimentos \(\rm{A}\), \(\rm{B}\),...
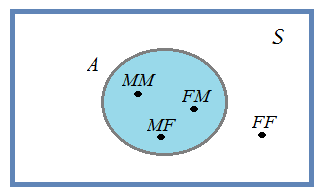
Consideremos, por exemplo, a experiência aleatória que consiste em verificar o sexo dos filhos das famílias com 2 filhos. O espaço de resultados é constituído pelos resultados S \(= \rm{\{ MM, MF, FM, FF \}}\). Seja \(A\) o acontecimento “Pelo menos um dos filhos é do sexo masculino”. Representando num diagrama de Venn, temos
Notas históricas
Os diagramas de Venn foram desenvolvidos pelo matemático britânico John Venn
Ver
Criada em 27 de Fevereiro de 2012
Revista em 02 de Janeiro de 2013
Aceite pelo editor em 02 de Janeiro de 2013