Movimento rectilíneo uniforme
Referência : Araújo, M., (2013) Movimento retilíneo uniforme, Rev. Ciência Elem., V1(1):016
Autor: Mariana de Araújo
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2013.016]

Uma partícula, de massa constante, livre de forças ou sujeita a um sistema de forças com resultante nula, mantém a sua velocidade constante, descrevendo uma trajectória rectilínea (ver Segunda Lei da dinâmica de Newton). Neste caso, diz-se que a partícula tem movimento rectilíneo uniforme. O termo "uniforme" diz respeito ao facto do valor da velocidade não se alterar.
Lei das velocidades
Uma vez que a resultante do sistema de forças que actua na partícula é nula, a aceleração também é nula1. Assim, num movimento rectilíneo uniforme a velocidade é constante - lei das velocidades.
Matematicamente, podemos excrever:
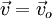 ,
,
sendo 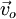 a velocidade no instante inicial.
a velocidade no instante inicial.
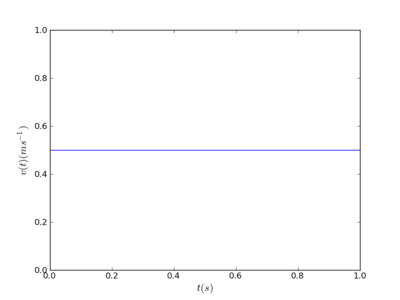
O gráfico do valor da velocidade em função do tempo é, pois, uma recta horizontal, podendo ser esboçado como se mostra na figura 1.
Lei dos espaços
Uma vez que a velocidade é constante, a partícula descreve uma trajectória rectilínea sem inversão. Assim, o módulo do deslocamento, 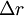 , que o corpo efectua num dado intervalo de tempo
, que o corpo efectua num dado intervalo de tempo 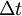 , é igual ao espaço percorrido,
, é igual ao espaço percorrido, 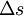 , nesse mesmo intervalo de tempo. Lembremos que a velocidade é a taxa temporal com que a partícula se desloca. Neste caso, como o movimento é uniforme, a taxa temporal de deslocamento é constante e é igual ao valor da velocidade média:
, nesse mesmo intervalo de tempo. Lembremos que a velocidade é a taxa temporal com que a partícula se desloca. Neste caso, como o movimento é uniforme, a taxa temporal de deslocamento é constante e é igual ao valor da velocidade média:
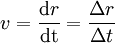
Uma vez que não há alteração da direcção da velocidade, o valor da velocidade é igual à taxa temporal média com que a partícula percorre o espaço:
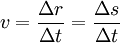
Atendendo à última igualdade, verificamos que num movimento rectilíneo uniforme o espaço percorrido é directamente proporcional ao intervalo de tempo gasto a percorrê-lo:
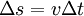 (1)
(1)
Uma outra forma de se chegar a este resultado seria interpretar o gráfico velocidade em função do tempo. A área entre o gráfico da função v(t) e o eixo do tempo entre os instantes 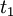 e
e 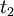 é igual ao espaço percorrido nesse intervalo de tempo. Assim sendo:
é igual ao espaço percorrido nesse intervalo de tempo. Assim sendo:
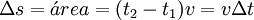
Que é igual à equação (1).
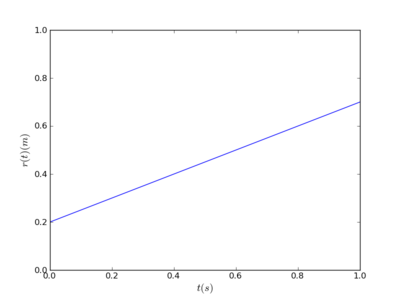
O gráfico das posições em função do tempo está esboçado na figura 2.
Admitindo que a trajectória do corpo coincide com o eixo dos xx, a equação das posições pode escrever-se do seguinte modo:
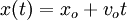 ,
,
sendo 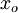 , a posição inicial da partícula.
, a posição inicial da partícula.
Criada em 01 de Agosto de 2011
Revista em 14 de Agosto de 2011
Aceite pelo editor em 14 de Agosto de 2011