Leis da refração da luz

Referência : Paiva, R., (2014) Leis da refração da luz, Rev. Ciência Elem., V2(3):203
Autores: Rodrigo de Paiva
Editor: M. A. Salgueiro da Silva
DOI: [http://doi.org/10.24927/rce2014.203]

---

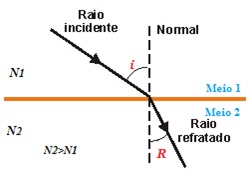
Consideremos um raio de luz monocromática propagando-se de um meio de índice de refração n₁ para um outro meio com maior índice de refração, n₂ (Figura 1). Seja i o ângulo de incidência. Devido à refração na interface dos dois meios, o raio incidente dá origem a um raio refratado que se propaga no segundo meio. O raio refratado forma com a normal um ângulo R, denominado ângulo de refração.

Figura 1 - Refração da luz na interface de dois meios com índices de refração diferentes.

OBS:  Se n₁ < n₂ , o ângulo de incidência ( i ) será maior que o ângulo de refração ( R ).
          Se n₁ > n₂ , o ângulo de incidência ( i ) será menor que o ângulo de refração ( R ).
          Se n₁ = n₂ , o ângulo de incidência ( i ) será igual ao ângulo de refração ( R ).

A refração da luz é regida por duas leis:

  1ª Lei : O raio incidente, o raio refratado e a normal à superfície de separação dos dois meios pertencem ao mesmo plano.
  2ª Lei ou Lei de Snell-Descartes: Os ângulos de incidência e de refração satisfazem a condição:

                  $\displaystyle n_1 \sin \left ( i \right ) = n_2 \sin \left ( R \right )$

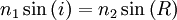
Assim, se n₂ > n₁, então sin( R ) < sin( i ), resultando R  <  i. Portanto, para incidência oblíqua da luz, quando esta passa de um meio com menor índice de refração para outro com maior índice, o raio luminoso aproxima-se da normal.

Podemos, também, escrever a lei de Snell-Descartes na forma :

                  $n_{21} = {n_2 \over n_1} = {\sin \left ( i \right ) \over \sin \left ( R \right )}$

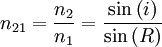
Em que n₂₁ é o índice de refração relativo do meio 2 em relação ao meio 1.

Referências

1. Francisco R. Júnior, Nicolau G. Ferraro, Paulo T. Soares, Os Fundamentos da Física 2, 8ª ed., Editora Moderna, São Paulo, 2003.
2. Paul A. Tipler, Gene Mosca, Física para Cientistas e Engenheiros, 6ª ed., Vol. 2, Editora LTC, 2009.

---

Criada em 17 de Junho de 2012
Revista em 12 de Novembro de 2012
Aceite pelo editor em 12 de Novembro de 2012