Diferenças entre edições de "Relações trigonométricas num triângulo retângulo"
| Linha 4: | Linha 4: | ||
<span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Rodrigue|José Francisco Rodrigues]]</i></span><br> | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Rodrigue|José Francisco Rodrigues]]</i></span><br> | ||
<b>DOI</b>: <i>[[http://doi.org/10.24927/rce2013.023 http://doi.org/10.24927/rce2013.023]]</i></span><br> | <b>DOI</b>: <i>[[http://doi.org/10.24927/rce2013.023 http://doi.org/10.24927/rce2013.023]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/pdf/2013/023/" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
---- | ---- | ||
==Razões trigonométricas== | ==Razões trigonométricas== | ||
Edição actual desde as 16h59min de 6 de junho de 2019
Referência : Tavares, J.N., (2013) Relações trigonométricas num triângulo retângulo, Rev. Ciência Elem., V1(1):023
Autores: João Nuno Tavares
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2013.023]

Razões trigonométricas
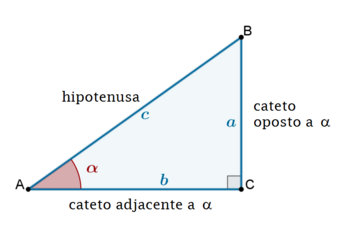
Seja \(\alpha\) um ângulo agudo \((0<\alpha<90º)\) de um triângulo retângulo, como se mostra no applet, podemos definir as três razões trigonométricas como:
\(\sin\alpha =\displaystyle \frac{\mbox{comprimento do cateto oposto}}{\mbox{comprimento da hipotenusa}} = \frac{a}{c}\)
\(\cos\alpha =\displaystyle \frac{\mbox{comprimento do cateto adjacente}}{\mbox{comprimento da hipotenusa}} = \frac{b}{c}\)
\(\tan\alpha =\displaystyle \frac{\mbox{comprimento do cateto oposto}}{\mbox{comprimento do lado adjacente}} = \frac{a}{b}\)
Fórmula Fundamental da Trigonometria
A Fórmula Fundamental da Trigonometria é uma consequência direta da aplicação do Teorema de Pitágoras ao triângulo retângulo da figura 1. Assim,
\((\mbox{hipotenusa})^2 = (\mbox{cateto oposto})^2+(\mbox{cateto adjacente})^2\)
Usando as letras da figura obtemos,
\(c^2=a^2+b^2\)
Dividindo ambos os membros da equação por \(a^2\neq 0\) concluímos, então, que \(1=\displaystyle \left(\frac{a}{c}\right)^2 + \left(\frac{b}{c}\right)^2 = \sin^2\alpha+\cos^2\alpha \), isto é,
| \[\qquad \sin^2\alpha+\cos^2\alpha=1\qquad\] |
Outras relações
Considerando agora a divisão das razões trigonométricas \(\sin\alpha\) e \(\cos\alpha\) obtemos, \(\displaystyle\frac{\sin\alpha}{\cos\alpha} = {\Large\frac{\frac{a}{c}}{\frac{b}{c}}}=\frac{a}{b}=\tan\alpha \), isto é,
| \[\quad\tan\alpha=\displaystyle\frac{\sin\alpha}{\cos\alpha}\qquad\] |
Olhando novamente para a fórmula fundamental da trigonometria, \(\sin^2\alpha+\cos^2\alpha=1\), e aplicando a ambos os membros da mesma uma divisão por \(\,\cos^2\alpha\,\) obtemos mais uma relação trigonométrica:
| \[\qquad\tan^2\alpha + 1 = \frac{1}{\cos^2\alpha}\qquad\] |
| Considerando esta aplicação podemos verificar mais algumas relações trigonométricas, neste caso, entre os dois ângulos agudos do triângulo retângulo representado, \(\alpha\) e \(\beta\).
Resulta facilmente do facto da soma dos ângulos internos de um triângulo ser \(180º\) que \(\alpha+\beta=90º\). Como se mostra na aplicação:
Mova os pontos B e C e verifique a validade das relações estabelecidas acima. |
Criada em 09 de Novembro de 2012
Revista em 27 de Dezembro de 2012
Aceite pelo editor em 27 de Dezembro de 2012