Diferenças entre edições de "Função quadrática"
| (98 edições intermédias de 2 utilizadores não apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | <span style="font-size:8pt"><b>Referência : </b> | + | <span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) '' Função quadrática'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(1):069 |
<br> | <br> | ||
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | <span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | ||
| − | <span style="font-size:8pt"><b>Editor</b>: <i> | + | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Jfgomes47|José Ferreira Gomes]]</i></span><br> |
| + | <span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.069 https://doi.org/10.24927/rce2017.069]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-069.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
| + | ---- | ||
| − | |||
==Definição== | ==Definição== | ||
Uma função \(f: \mathbb{R} \longrightarrow \mathbb{R}\) chama-se uma ''função quadrática'' quando existem números reais \(a\), \(b\) e \(c\), com \(a \neq 0\), tais que \(f(x)=ax^2+bx+c\) para todo \(x \in \mathbb{R}\). | Uma função \(f: \mathbb{R} \longrightarrow \mathbb{R}\) chama-se uma ''função quadrática'' quando existem números reais \(a\), \(b\) e \(c\), com \(a \neq 0\), tais que \(f(x)=ax^2+bx+c\) para todo \(x \in \mathbb{R}\). | ||
| − | |||
==Propriedades== | ==Propriedades== | ||
| − | + | '''Sinal:''' | |
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | A função quadrática tem no máximo dois zeros. Determinar os zeros de uma função quadrática é equivalente a resolver a equação do 2ºgrau \(ax^2+bx+c=0\), assim poderá ser necessário recorrer à [[Fórmulas resolventes|fórmula resolvente]] para equações do 2ºgrau. | ||
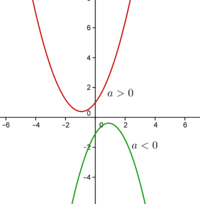
| − | + | * Se o discriminante \(\Delta=b^2-4ac\) for negativo, a função quadrática não tem zeros e portanto ou é sempre positiva ou sempre negativa. Se \(a >0\) a função é positiva para \(x \in \mathbb{R}\), pelo contrário se o coeficiente \(a<0\) então a função é negativa em todo o seu domínio. Ver figura 1. | |
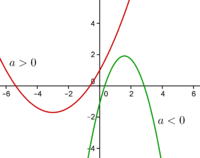
| − | * Se | + | * Se \(\Delta>0\) a função tem dois zeros, respetivamente: \(x_1=(-b-\sqrt{\Delta})/2a\quad\) ; \(\quad x_2=(-b+\sqrt{\Delta})/2a \quad\) com \(x_1<x_2\). Neste caso, se \(a>0\) a função é positiva no intervalo \(]-\infty,x_1[ \, \cup \, ]x_2,+\infty[\) e negativa para \(x \in \, ]x_1,x_2[\). Já se \(a<0\) a função toma valores positivos para \(x \in \, ]x_1,x_2[\) e valores negativos no intervalo \(]-\infty,x_1[ \, \cup \, ]x_2,+\infty[\). Ver figura 2. |
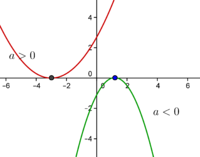
| − | * | + | * Finalmente se \(\Delta=0\) a função quadrática possui um único zero em \(x=-b/2a\). Neste caso, se \(a>0\) a função é positiva em \(x \in \, \mathbb{R} \backslash \{-b/2a\}\). Já se \(a<0\), a função é negativa em \(x \in \, \mathbb{R} \backslash \{-b/2a\}\). Ver figura 3. |
| + | | | ||
| + | | | ||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(a>0\) e zeros={\(x_1\), \(x_2\)}''' | ||
| + | |- | ||
| + | ! style="background: #F5F5DC;" | \[x\] | ||
| + | ! style="background: #F5F5DC;" | \[-\infty\] | ||
| + | ! style="background: #F5F5DC;" | \[x_1\] | ||
| + | ! style="background: #F5F5DC;" | \[\quad\] | ||
| + | ! style="background: #F5F5DC;" | \[x_2\] | ||
| + | ! style="background: #F5F5DC;" | \[+\infty\] | ||
| + | |- | ||
| + | | \(f(x)\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |} | ||
| − | |||
| − | + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | |
| + | |+'''\(a<0\) e zeros={\(x_1\), \(x_2\)}''' | ||
| + | |- | ||
| + | ! style="background: #F5F5DC;" | \[x\] | ||
| + | ! style="background: #F5F5DC;" | \[-\infty\] | ||
| + | ! style="background: #F5F5DC;" | \[x_1\] | ||
| + | ! style="background: #F5F5DC;" | \[\quad\] | ||
| + | ! style="background: #F5F5DC;" | \[x_2\] | ||
| + | ! style="background: #F5F5DC;" | \[+\infty\] | ||
| + | |- | ||
| + | | \(f(x)\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |} | ||
| − | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | [[Ficheiro:Fquadratica.png|thumb|right|200px|'''Figura 1 -''']] || [[Ficheiro:Fquadratica2.png|thumb|right|200px|'''Figura 2 -''']] || [[Ficheiro:Fquadratica3.png|thumb|right|200px|'''Figura 3 -''']] | ||
| + | |} | ||
| + | '''Monotonia:''' | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Suponhamos \(a>0\) e consideremos a forma canónica para a função quadrática \(f(x)\), | ||
| + | |||
| + | \(\displaystyle f(x)=ax^2+bx+c=a\left[ \left( x+\frac{b}{2a} \right)^2+ \frac{4ac-b^2}{4a^2} \right]\) | ||
| + | |||
| + | Considerando a soma da duas parcelas no interior dos parêntesis retos, verificamos que a primeira depende de \(x\) e é sempre positiva. A segunda parcela é constante. Portanto, o menor valor desta soma é atingido quando \(\displaystyle \left( x+\frac{b}{2a} \right)^2\) é igual a zero, ou seja, quando \(x=-b/2a\). Neste ponto, \(f(x)\) também assume o seu valor mínimo. Concluímos assim que, quando \(a>0\) o menor valor (mínimo da função) assumido por \(f(x)\) é: \(f(-b/2a)=c-(b^2/4a)\). | ||
| + | |||
| + | Se \(a<0\), o valor \(f(-b/2a)\) é o maior dos números \(f(x)\) (máximo da função), para qualquer \(x \in \mathbb{R}\). | ||
| + | |||
| + | Quando \(a>0\), \(f(x)=ax^2+bx+c\) não assume valor máximo, é assim uma função ilimitada superiormente. Analogamente, quando \(a<0\), \(f(x)\) não assume valor mínimo sendo assim uma função ilimitada inferiormente. | ||
| + | | | ||
| + | | | ||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''Se \(a>0\)''' | ||
| + | |- | ||
| + | ! style="background: #CAE1FF;" | \[x\] | ||
| + | ! style="background: #CAE1FF;" | \[-\infty\] | ||
| + | ! style="background: #CAE1FF;" | \[-b/2a\] | ||
| + | ! style="background: #CAE1FF;" | \[+\infty\] | ||
| + | |- | ||
| + | | \(f(x)\) | ||
| + | | \(\searrow\) | ||
| + | | Mín. | ||
| + | \(f(-b/2a)\) | ||
| + | | \(\nearrow\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''Se \(a<0\)''' | ||
| + | |- | ||
| + | ! style="background: #CAE1FF;" | \[x\] | ||
| + | ! style="background: #CAE1FF;" | \[-\infty\] | ||
| + | ! style="background: #CAE1FF;" | \[-b/2a\] | ||
| + | ! style="background: #CAE1FF;" | \[+\infty\] | ||
| + | |- | ||
| + | | \(f(x)\) | ||
| + | | \(\nearrow\) | ||
| + | | Máx. | ||
| + | \(f(-b/2a)\) | ||
| + | | \(\searrow\) | ||
| + | |} | ||
| + | |} | ||
==Representação gráfica== | ==Representação gráfica== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | O gráfico de uma função quadrática é uma parábola. A concavidade da parábola é determinada pelo valor de \(a\). Se \(a>0\) a concavidade da parábola que representa a função quadrática é voltada para cima, se \(a<0\) a concavidade da parábola é voltada para baixo. | ||
| + | A ordenada do ponto de interseção da parábola com o eixo dos \(yy\) é dado pelo valor de \(c\) pois, nesse ponto de interseção a abcissa é nula, ou seja \(x=0\), logo \(f(0)=a \times 0^2+b\times 0+c=c\). | ||
| + | |||
| + | O '''vértice''' da parábola é o ponto onde a função quadrática toma o seu valor máximo (quando \(a<0\)) ou mínimo (quando \(a>0\)). Portanto as coordenadas deste ponto correspondem ao maximizante e máximo da função ou ao minimizante e mínimo da função, respetivamente. As coordenadas do vértice da parábola são \(\displaystyle \left(\frac{-b}{2a}, f\left(\frac{-b}{2a}\right)\right)=\left(\frac{-b}{2a}, c-\frac{b^2}{4a}\right)\). | ||
| + | |||
| + | A reta de equação \(x=-b/2a\) define o <u>eixo de simetria</u> da parábola. Assim, o eixo de simetria da parábola contém sempre o vértice da mesma. | ||
| + | |||
| + | Os '''zeros''' da função quadrática são os pontos em que a função se anula, este pontos correspondem aos pontos de interseção da parábola com o eixo dos \(xx\). Como já foi estudado anteriormente a função quadrática pode ter no máximo dois zeros. | ||
| + | |||
| + | |||
| + | ''Mova os seletores a, b e c para alterar a função quadrática \(f(x)\). Verifique as propriedades acima enunciadas nomeadamente, as coordenadas dos pontos de interseção com os eixos coordenados. '' | ||
| + | || | ||
| + | <html><iframe scrolling="no" title="Função quadrática" src="https://www.geogebra.org/material/iframe/id/s2pdjcup/width/550/height/400/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="550px" height="400px" style="border:0px;"> </iframe></html> | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Aplicação== | ||
| + | |||
| + | A trajetória de um projétil lançado a partir de uma posição inicial \(P_o\), com uma velocidade inicial \({\bf v}_o\), é uma parábola. Estamos a supôr que a distância percorrida é pequena, que o projétil está apenas submetido à acção da força gravítica à superfície da terra suposta plana (não há atrito, por exemplo). | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <html><iframe scrolling="no" title="Função quadrática" src="https://www.geogebra.org/material/iframe/id/gycturn3/width/550/height/400/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="550px" height="400px" style="border:0px;"> </iframe></html> | ||
| + | || | ||
| + | ''Comece por mover o ponto \(P_0\) e estabelecer a posição inicial do projétil.'' | ||
| + | ''Mova os seletores \(v_0\), \(\theta\) e \(m\) para alterar respetivamente, a velocidade inicial \(v_0\) do projétil, o ângulo \(\theta\) que o vetor velocidade inicial faz com a parte positiva do eixo dos xx, e a massa \(m\) do projétil.'' | ||
| + | ''O seletor \(g\) permite variar a aceleração da gravidade (em \(m/s^2\)). Por exemplo, à superfície da terra \(g=9.8 m/s^2\). Finalmente, \(t\) indica o tempo decorrido após o lançamento do projétil.'' | ||
| + | |||
| + | ''Clique no botão'' <u>play</u> '' para observar o movimento do projétil. Note que a trajectória é independente da massa \(m\) do projétil!'' | ||
| + | |} | ||
| + | |||
| + | ==Ver também== | ||
| + | |||
| + | * [[Equação do 2º grau]]; | ||
| + | |||
| + | |||
| + | ==Referências== | ||
| − | + | * LIMA, Elon Lages, CARVALHO Paulo Cezar, WAGNER Eduardo, MORGADO Augusto César (1997) ''"A Matemática do Ensino Médio - Volume 1"'' 2ªedição, Coleção do Professor de Matemática, Sociedade Brasileira de Matemática, Rio de Janeiro; | |
| − | [[Category: | + | ---- <br>Criada em 30 de Maio de 2013<br> Revista em 27 de Junho de 2013<br> Aceite pelo editor em 31 de Março de 2017<br> |
| + | [[Category:Matemática]] | ||
Edição actual desde as 10h13min de 8 de julho de 2021
Referência : Tavares, J., Geraldo, A., (2017) Função quadrática, Rev. Ciência Elem., V5(1):069
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.069]

Índice |
Definição
Uma função \(f: \mathbb{R} \longrightarrow \mathbb{R}\) chama-se uma função quadrática quando existem números reais \(a\), \(b\) e \(c\), com \(a \neq 0\), tais que \(f(x)=ax^2+bx+c\) para todo \(x \in \mathbb{R}\).
Propriedades
Sinal:
A função quadrática tem no máximo dois zeros. Determinar os zeros de uma função quadrática é equivalente a resolver a equação do 2ºgrau \(ax^2+bx+c=0\), assim poderá ser necessário recorrer à fórmula resolvente para equações do 2ºgrau.
|
|
Monotonia:
| Suponhamos \(a>0\) e consideremos a forma canónica para a função quadrática \(f(x)\),
\(\displaystyle f(x)=ax^2+bx+c=a\left[ \left( x+\frac{b}{2a} \right)^2+ \frac{4ac-b^2}{4a^2} \right]\) Considerando a soma da duas parcelas no interior dos parêntesis retos, verificamos que a primeira depende de \(x\) e é sempre positiva. A segunda parcela é constante. Portanto, o menor valor desta soma é atingido quando \(\displaystyle \left( x+\frac{b}{2a} \right)^2\) é igual a zero, ou seja, quando \(x=-b/2a\). Neste ponto, \(f(x)\) também assume o seu valor mínimo. Concluímos assim que, quando \(a>0\) o menor valor (mínimo da função) assumido por \(f(x)\) é: \(f(-b/2a)=c-(b^2/4a)\). Se \(a<0\), o valor \(f(-b/2a)\) é o maior dos números \(f(x)\) (máximo da função), para qualquer \(x \in \mathbb{R}\). Quando \(a>0\), \(f(x)=ax^2+bx+c\) não assume valor máximo, é assim uma função ilimitada superiormente. Analogamente, quando \(a<0\), \(f(x)\) não assume valor mínimo sendo assim uma função ilimitada inferiormente. |
|
Representação gráfica
| O gráfico de uma função quadrática é uma parábola. A concavidade da parábola é determinada pelo valor de \(a\). Se \(a>0\) a concavidade da parábola que representa a função quadrática é voltada para cima, se \(a<0\) a concavidade da parábola é voltada para baixo.
A ordenada do ponto de interseção da parábola com o eixo dos \(yy\) é dado pelo valor de \(c\) pois, nesse ponto de interseção a abcissa é nula, ou seja \(x=0\), logo \(f(0)=a \times 0^2+b\times 0+c=c\). O vértice da parábola é o ponto onde a função quadrática toma o seu valor máximo (quando \(a<0\)) ou mínimo (quando \(a>0\)). Portanto as coordenadas deste ponto correspondem ao maximizante e máximo da função ou ao minimizante e mínimo da função, respetivamente. As coordenadas do vértice da parábola são \(\displaystyle \left(\frac{-b}{2a}, f\left(\frac{-b}{2a}\right)\right)=\left(\frac{-b}{2a}, c-\frac{b^2}{4a}\right)\). A reta de equação \(x=-b/2a\) define o eixo de simetria da parábola. Assim, o eixo de simetria da parábola contém sempre o vértice da mesma. Os zeros da função quadrática são os pontos em que a função se anula, este pontos correspondem aos pontos de interseção da parábola com o eixo dos \(xx\). Como já foi estudado anteriormente a função quadrática pode ter no máximo dois zeros.
|
|
Aplicação
A trajetória de um projétil lançado a partir de uma posição inicial \(P_o\), com uma velocidade inicial \({\bf v}_o\), é uma parábola. Estamos a supôr que a distância percorrida é pequena, que o projétil está apenas submetido à acção da força gravítica à superfície da terra suposta plana (não há atrito, por exemplo).
|
Comece por mover o ponto \(P_0\) e estabelecer a posição inicial do projétil. Mova os seletores \(v_0\), \(\theta\) e \(m\) para alterar respetivamente, a velocidade inicial \(v_0\) do projétil, o ângulo \(\theta\) que o vetor velocidade inicial faz com a parte positiva do eixo dos xx, e a massa \(m\) do projétil. O seletor \(g\) permite variar a aceleração da gravidade (em \(m/s^2\)). Por exemplo, à superfície da terra \(g=9.8 m/s^2\). Finalmente, \(t\) indica o tempo decorrido após o lançamento do projétil. Clique no botão play para observar o movimento do projétil. Note que a trajectória é independente da massa \(m\) do projétil! |
Ver também
Referências
- LIMA, Elon Lages, CARVALHO Paulo Cezar, WAGNER Eduardo, MORGADO Augusto César (1997) "A Matemática do Ensino Médio - Volume 1" 2ªedição, Coleção do Professor de Matemática, Sociedade Brasileira de Matemática, Rio de Janeiro;
Criada em 30 de Maio de 2013
Revista em 27 de Junho de 2013
Aceite pelo editor em 31 de Março de 2017