Diferenças entre edições de "Referenciais"
(→Ortogonal e normado) |
|||
| (54 edições intermédias de 2 utilizadores não apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | <span style="font-size:8pt"><b>Referência : </b> | + | <span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) '' Referenciais'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(2):072 |
<br> | <br> | ||
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | <span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | ||
| − | <span style="font-size:8pt"><b>Editor</b>: <i> | + | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Jfgomes47|José Ferreira Gomes]]</i></span><br> |
| + | <span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.072 https://doi.org/10.24927/rce2017.072]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-072.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
| + | ---- | ||
| − | |||
__TOC__ | __TOC__ | ||
| Linha 12: | Linha 15: | ||
{| class="wikitable" cellspacing="20" | {| class="wikitable" cellspacing="20" | ||
|- | |- | ||
| − | | < | + | | <html><iframe scrolling="no" title="Referenciais" src="https://www.geogebra.org/material/iframe/id/bdhax43n/width/390/height/100/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="390px" height="100px" style="border:0px;"> </iframe></html> |
| || | | || | ||
Um '''referencial cartesiano''' (afim) numa reta \(r\), é definido por dois pontos distintos \(O,U\in r\). \(O\) diz-se a '''origem''' e \(U\) o '''ponto unidade''' do referencial. O vector \(\overrightarrow{OU}\) diz-se o vector unitário do referencial e define uma orientação na reta: positiva quando esta é percorrida de \(O\) para \(U\) e negativa no outro caso. | Um '''referencial cartesiano''' (afim) numa reta \(r\), é definido por dois pontos distintos \(O,U\in r\). \(O\) diz-se a '''origem''' e \(U\) o '''ponto unidade''' do referencial. O vector \(\overrightarrow{OU}\) diz-se o vector unitário do referencial e define uma orientação na reta: positiva quando esta é percorrida de \(O\) para \(U\) e negativa no outro caso. | ||
|} | |} | ||
| − | O referencial \(\mathcal{R}=(O,U)\), permite estabelecer uma correspondência bijectiva entre os pontos da reta \(r\) e o conjunto dos números reais. De facto, dado um ponto qualquer \(A\in r\), o vector \(\overrightarrow{OA}\) é colinear com \(\overrightarrow{OU}\) e, por isso, existe um e só número real \(a\in\mathbb{R}\) tal que \(\overrightarrow{OA} =a\ \overrightarrow{OU} \). Este número \(a\) é a chamada '''coordenada''' (afim) de \(A\) relativamente ao referencial \(\mathcal{R}\). Em particular, a coordenada do ponto \(O\) é \(0\) e a coordenada do ponto \(U\) é \(1\) (veja o applet. Comece por seleccionar \(U\) e depois mova o ponto \(A\). A coordenada de \(A\) é o número \(a\) indicado no applet, aproximado às 3 casas decimais). | + | O referencial \(\mathcal{R}=(O,U)\), permite estabelecer uma correspondência bijectiva entre os pontos da reta \(r\) e o conjunto dos números reais. De facto, dado um ponto qualquer \(A\in r\), o vector \(\overrightarrow{OA}\) é colinear com \(\overrightarrow{OU}\) e, por isso, existe um e só número real \(a\in\mathbb{R}\) tal que \(\overrightarrow{OA} =a\ \overrightarrow{OU} \). Este número \(a\) é a chamada '''coordenada''' (afim) de \(A\) relativamente ao referencial \(\mathcal{R}\). Em particular, a coordenada do ponto \(O\) é \(0\) e a coordenada do ponto \(U\) é \(1\) ''(veja o applet. Comece por seleccionar \(U\) e depois mova o ponto \(A\). A coordenada de \(A\) é o número \(a\) indicado no applet, aproximado às 3 casas decimais)''. |
| − | + | ||
=Referencial Cartesiano no plano= | =Referencial Cartesiano no plano= | ||
| Linha 24: | Linha 26: | ||
{| class="wikitable" cellspacing="15" | {| class="wikitable" cellspacing="15" | ||
|- | |- | ||
| − | | < | + | | <html><iframe scrolling="no" title="Referenciais" src="https://www.geogebra.org/material/iframe/id/mrhuuc8s/width/480/height/390/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="480px" height="390px" style="border:0px;"> </iframe></html> |
| || | | || | ||
Um '''referencial cartesiano''' (afim) no plano é um sistema constituído por 3 pontos \(O,I,J\) não colineares. \(O\) diz-se a <span style="color:red">'''origem do referencial'''</span>. Os outros dois pontos determinam duas retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\) e \(\overrightarrow{OJ}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\) e de \(O\) para \(J\), respetivamente, e negativa nos outros casos. | Um '''referencial cartesiano''' (afim) no plano é um sistema constituído por 3 pontos \(O,I,J\) não colineares. \(O\) diz-se a <span style="color:red">'''origem do referencial'''</span>. Os outros dois pontos determinam duas retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\) e \(\overrightarrow{OJ}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\) e de \(O\) para \(J\), respetivamente, e negativa nos outros casos. | ||
| − | Dado um ponto \(P\) do plano, por este ponto traçamos uma reta | + | Dado um ponto \(P\) do plano, por este ponto traçamos uma reta paralela a cada um dos eixos orientados. Encontramos assim os pontos \(A\) e \(B\), pontos de intersecção dessas retas com os eixos orientados (como se ilustra no applet). Estes pontos definem dois vetores, o vetor \(\overrightarrow{OA}\) colinear com \(\overrightarrow{OI}\), \(\overrightarrow{OA}=x \, \overrightarrow{OI}\), \(x \in \mathbb{R}\), e o vetor \(\overrightarrow{OB}\) colinear com \(\overrightarrow{OJ}\), \(\overrightarrow{OB}=y \, \overrightarrow{OJ}\), com \(y \in \mathbb{R}\). |
Os números \(x\) e \(y\) são então as '''coordenadas''' do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J)\). | Os números \(x\) e \(y\) são então as '''coordenadas''' do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J)\). | ||
| Linha 50: | Linha 52: | ||
Um referencial cartesiano no plano serve para estudar geometria plana com ajuda de álgebra, isto é, estudar Geometria Analítica em duas dimensões (2D). | Um referencial cartesiano no plano serve para estudar geometria plana com ajuda de álgebra, isto é, estudar Geometria Analítica em duas dimensões (2D). | ||
| − | As figuras do plano, tais como, retas, curvas, polígonos, e outros lugares geométricos, podem então ser descritos por equações ou inequações nas variáveis \(x\) e \(y\), onde \(P(x,y)\) designa um ponto genérico desse lugar. | + | As figuras do plano, tais como, retas, curvas, polígonos, e outros lugares geométricos, podem então ser descritos por (sistemas de) equações ou inequações nas variáveis \(x\) e \(y\), onde \(P(x,y)\) designa um ponto genérico desse lugar. |
==Ortogonal e normado== | ==Ortogonal e normado== | ||
| + | Quando no plano \(\mathbb{R}^2\) está definida uma [[Produto escalar|estrutura Euclideana]] e portanto as noções de ortogonalidade, ângulo, comprimento, etc. faz sentido falar em referenciais ortogonais e/ou normados. | ||
| − | + | {| border="0" cellspacing="20" | |
| + | |- | ||
| + | | | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | O referencial denomina-se de '''ortogonal''' quando os vetores unitários são ortogonais, ou seja, quando o ângulo entre esses dois vetores é um ângulo reto (amplitude \(90º\)). |
| + | ''Mova as extremidades dos vetores \(\vec i\) e \(\vec j\) para obter diferentes referenciais ortogonais. Verifique que a norma desses vetores é diferente o ângulo entre os mesmo é sempre de \(90º\).'' | ||
| + | || | ||
| + | <html><iframe scrolling="no" title="Referenciais" src="https://www.geogebra.org/material/iframe/id/ack8tpdc/width/220/height/190/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="220px" height="190px" style="border:0px;"> </iframe></html> | ||
| + | |} | ||
| + | || | ||
| + | {| class="wikitable" | ||
|- | |- | ||
| − | | | + | | Se os vetores unitários, \(\vec i\) e \(\vec j\), têm a mesma norma, ou seja, o mesmo comprimento, dizemos que o referencial é '''normado'''. |
| + | ''No applet mova as extremidades dos vetores \(\vec i\) e \(\vec j\) para obter diferentes referenciais normados. Verifique que ao mover esses pontos pode também alterar a norma dos vetores, que é sempre igual para os dois vetores.'' | ||
| + | || | ||
| + | <html><iframe scrolling="no" title="Referenciais" src="https://www.geogebra.org/material/iframe/id/ktcva6cu/width/220/height/190/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="220px" height="190px" style="border:0px;"> </iframe></html> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Um referencial '''ortonormado''' é um referencial que é simultaneamente <u>ortogonal</u> e <u>normado</u>. | ||
| + | ''Mova a extremidade do vetor \(\vec j\) para obter diferentes referenciais ortonormados''. | ||
| + | || | ||
| + | <html><iframe scrolling="no" title="Referenciais" src="https://www.geogebra.org/material/iframe/id/uyhwm6at/width/220/height/190/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="220px" height="190px" style="border:0px;"> </iframe></html> | ||
| + | |} | ||
|} | |} | ||
=Referencial Cartesiano no espaço= | =Referencial Cartesiano no espaço= | ||
| − | |||
| Linha 74: | Linha 97: | ||
Um '''referencial cartesiano''' (afim) no espaço é um sistema constituído por 4 pontos \(O,I,J,K\) não colineares. \(O\) diz-se a <span style="color:red">'''origem do referencial'''</span>. Os outros três pontos determinam três retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\), \(\overrightarrow{OJ}\) e \(\overrightarrow{OK}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\), de \(O\) para \(J\) e de \(O\) para \(K\), respetivamente, e negativa nos outros casos. | Um '''referencial cartesiano''' (afim) no espaço é um sistema constituído por 4 pontos \(O,I,J,K\) não colineares. \(O\) diz-se a <span style="color:red">'''origem do referencial'''</span>. Os outros três pontos determinam três retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\), \(\overrightarrow{OJ}\) e \(\overrightarrow{OK}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\), de \(O\) para \(J\) e de \(O\) para \(K\), respetivamente, e negativa nos outros casos. | ||
| − | Dado um ponto \(P\) do espaço, por este ponto fazemos passar um plano | + | Dado um ponto \(P\) do espaço, por este ponto fazemos passar um plano paralelo a cada um dos eixos orientados. Encontramos assim os pontos \(A\), \(B\) e \(C\), pontos de intersecção dos três planos com os eixos orientados. Estes pontos definem três vetores, o vetor \(\overrightarrow{OA}\) colinear com \(\overrightarrow{OI}\), \(\overrightarrow{OA}=x \, \overrightarrow{OI}\), \(x \in \mathbb{R}\), o vetor \(\overrightarrow{OB}\) colinear com \(\overrightarrow{OJ}\), \(\overrightarrow{OB}=y \, \overrightarrow{OJ}\), com \(y \in \mathbb{R}\) e o vetor \(\overrightarrow{OC}\) colinear com \(\overrightarrow{OK}\), \(\overrightarrow{OC}=z \, \overrightarrow{OK}\), com \(z \in \mathbb{R}\). |
Os números \(x\), \(y\) e \(z\) são então as '''coordenadas''' do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J,K)\). | Os números \(x\), \(y\) e \(z\) são então as '''coordenadas''' do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J,K)\). | ||
| Linha 95: | Linha 118: | ||
Um referencial cartesiano no espaço serve para estudar geometria espacial com ajuda de álgebra, isto é, estudar Geometria Analítica em três dimensões (3D). | Um referencial cartesiano no espaço serve para estudar geometria espacial com ajuda de álgebra, isto é, estudar Geometria Analítica em três dimensões (3D). | ||
| − | As figuras do espaço, tais como, retas, planos, curvas, superfícies, poliedros, e outros lugares geométricos, podem então ser descritos por equações ou inequações nas variáveis \(x\), \(y\) e \(z\), onde \(P(x,y,z)\) designa um ponto genérico desse lugar. | + | As figuras do espaço, tais como, retas, planos, curvas, superfícies, poliedros, e outros lugares geométricos, podem então ser descritos por (sistemas de) equações ou inequações nas variáveis \(x\), \(y\) e \(z\), onde \(P(x,y,z)\) designa um ponto genérico desse lugar. |
| + | |||
| + | |||
| + | |||
=Quadrantes e Octantes= | =Quadrantes e Octantes= | ||
| Linha 139: | Linha 165: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =Referências= | ||
| + | |||
| + | <span style="color:#4169E1">\([1]\)</span> BARUK, Stella, ''Dictionnaire de Mathemátiques Elémentaires'', 1992, Editions du Seuil, traduzido por SILVA, Maria do Céu, MIRRA, Maria Elisa, RIBEIRO, Maria de Fátima, 2005, Edições Afrontamento. | ||
| + | |||
| + | |||
| + | ---- <br>Criada em 30 de Janeiro de 2013<br> Revista em 19 de Fevereiro de 2013<br> Aceite pelo editor em 30 de Junho de 2017<br> | ||
[[Category:Matemática]] | [[Category:Matemática]] | ||
Edição actual desde as 13h04min de 9 de julho de 2021
Referência : Tavares, J., Geraldo, A., (2017) Referenciais, Rev. Ciência Elem., V5(2):072
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.072]

Índice |
Referencial Cartesiano na reta
|
Um referencial cartesiano (afim) numa reta \(r\), é definido por dois pontos distintos \(O,U\in r\). \(O\) diz-se a origem e \(U\) o ponto unidade do referencial. O vector \(\overrightarrow{OU}\) diz-se o vector unitário do referencial e define uma orientação na reta: positiva quando esta é percorrida de \(O\) para \(U\) e negativa no outro caso. |
O referencial \(\mathcal{R}=(O,U)\), permite estabelecer uma correspondência bijectiva entre os pontos da reta \(r\) e o conjunto dos números reais. De facto, dado um ponto qualquer \(A\in r\), o vector \(\overrightarrow{OA}\) é colinear com \(\overrightarrow{OU}\) e, por isso, existe um e só número real \(a\in\mathbb{R}\) tal que \(\overrightarrow{OA} =a\ \overrightarrow{OU} \). Este número \(a\) é a chamada coordenada (afim) de \(A\) relativamente ao referencial \(\mathcal{R}\). Em particular, a coordenada do ponto \(O\) é \(0\) e a coordenada do ponto \(U\) é \(1\) (veja o applet. Comece por seleccionar \(U\) e depois mova o ponto \(A\). A coordenada de \(A\) é o número \(a\) indicado no applet, aproximado às 3 casas decimais).
Referencial Cartesiano no plano
|
Um referencial cartesiano (afim) no plano é um sistema constituído por 3 pontos \(O,I,J\) não colineares. \(O\) diz-se a origem do referencial. Os outros dois pontos determinam duas retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\) e \(\overrightarrow{OJ}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\) e de \(O\) para \(J\), respetivamente, e negativa nos outros casos. Dado um ponto \(P\) do plano, por este ponto traçamos uma reta paralela a cada um dos eixos orientados. Encontramos assim os pontos \(A\) e \(B\), pontos de intersecção dessas retas com os eixos orientados (como se ilustra no applet). Estes pontos definem dois vetores, o vetor \(\overrightarrow{OA}\) colinear com \(\overrightarrow{OI}\), \(\overrightarrow{OA}=x \, \overrightarrow{OI}\), \(x \in \mathbb{R}\), e o vetor \(\overrightarrow{OB}\) colinear com \(\overrightarrow{OJ}\), \(\overrightarrow{OB}=y \, \overrightarrow{OJ}\), com \(y \in \mathbb{R}\). Os números \(x\) e \(y\) são então as coordenadas do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J)\). A cada ponto \(P\) do plano associamos, de forma unívoca, o par de coordenadas relativas a esse sistema de eixos (ou referencial). \[P \quad \longleftrightarrow \quad (x,y) \in \mathbb{R}^2\] \(x\) diz-se a abcissa e \(y\) a ordenada do ponto \(P\). Escrevemos então:
No applet comece por selecionar \(I\) e \(J\) e depois mova o ponto \(P\), as coordenadas de \(P\) são os números \(x\) e \(y\) indicados com aproximação às milésimas. |
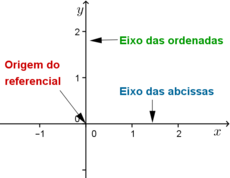
As duas retas orientadas são denominadas de eixos do referencial. Em particular, à reta orientada pelo vetor \(\overrightarrow{OI}\) chamamos de eixo das abcissas ou eixo dos \(xx\) e à reta orientada pelo vetor \(\overrightarrow{OJ}\) chamamos de eixo das ordenadas ou eixo dos \(yy\). Na figura 1 podemos ver a indicação de cada um dos eixos coordenados e da origem do referencial representado.
Um referencial cartesiano no plano serve para estudar geometria plana com ajuda de álgebra, isto é, estudar Geometria Analítica em duas dimensões (2D).
As figuras do plano, tais como, retas, curvas, polígonos, e outros lugares geométricos, podem então ser descritos por (sistemas de) equações ou inequações nas variáveis \(x\) e \(y\), onde \(P(x,y)\) designa um ponto genérico desse lugar.
Ortogonal e normado
Quando no plano \(\mathbb{R}^2\) está definida uma estrutura Euclideana e portanto as noções de ortogonalidade, ângulo, comprimento, etc. faz sentido falar em referenciais ortogonais e/ou normados.
|
| ||||
|
Referencial Cartesiano no espaço
|
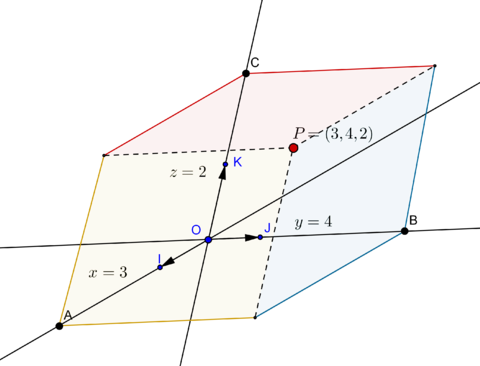
Um referencial cartesiano (afim) no espaço é um sistema constituído por 4 pontos \(O,I,J,K\) não colineares. \(O\) diz-se a origem do referencial. Os outros três pontos determinam três retas orientadas, respetivamente pelos vectores \(\overrightarrow{OI}\), \(\overrightarrow{OJ}\) e \(\overrightarrow{OK}\). A orientação de cada uma dessas retas é positiva quando são percorridas de \(O\) para \(I\), de \(O\) para \(J\) e de \(O\) para \(K\), respetivamente, e negativa nos outros casos. Dado um ponto \(P\) do espaço, por este ponto fazemos passar um plano paralelo a cada um dos eixos orientados. Encontramos assim os pontos \(A\), \(B\) e \(C\), pontos de intersecção dos três planos com os eixos orientados. Estes pontos definem três vetores, o vetor \(\overrightarrow{OA}\) colinear com \(\overrightarrow{OI}\), \(\overrightarrow{OA}=x \, \overrightarrow{OI}\), \(x \in \mathbb{R}\), o vetor \(\overrightarrow{OB}\) colinear com \(\overrightarrow{OJ}\), \(\overrightarrow{OB}=y \, \overrightarrow{OJ}\), com \(y \in \mathbb{R}\) e o vetor \(\overrightarrow{OC}\) colinear com \(\overrightarrow{OK}\), \(\overrightarrow{OC}=z \, \overrightarrow{OK}\), com \(z \in \mathbb{R}\). Os números \(x\), \(y\) e \(z\) são então as coordenadas do ponto \(P\) relativamente ao referencial \(\mathcal{R}=(O,I,J,K)\). A cada ponto \(P\) do espaço associamos, de forma unívoca, o terno de coordenadas relativas a esse sistema de eixos (ou referencial). \[P \quad \longleftrightarrow \quad (x,y,z) \in \mathbb{R}^3\] \(x\) diz-se a abcissa, \(y\) a ordenada e \(z\) a cota do ponto \(P\). Escrevemos então:
|
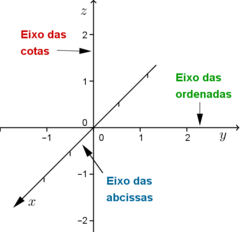
Da mesma forma que no plano, no espaço as três retas orientadas são também denominadas de eixos do referencial. A reta orientada por \(\overrightarrow{OI}\) é denominada de eixo das abcissas, a reta orientada por \(\overrightarrow{OJ}\) será o eixo das ordenadas e a reta orientada por \(\overrightarrow{OK}\) é chamada de eixo das cotas ou eixo dos \(zz\). Na figura 3 estão indicados cada um dos eixos coordenados do referencial representado.
Um referencial cartesiano no espaço serve para estudar geometria espacial com ajuda de álgebra, isto é, estudar Geometria Analítica em três dimensões (3D).
As figuras do espaço, tais como, retas, planos, curvas, superfícies, poliedros, e outros lugares geométricos, podem então ser descritos por (sistemas de) equações ou inequações nas variáveis \(x\), \(y\) e \(z\), onde \(P(x,y,z)\) designa um ponto genérico desse lugar.
Quadrantes e Octantes
Os eixos de um referencial cartesiano dividem o plano em quatro partes aos quais chamamos de quadrantes, existe por isso quatro quadrantes. A figura seguinte ilustra esse divisão.
|
Como se pode verificar pela figura ao lado, no \(1º\) e \(4º\) quadrantes as coordenadas têm o mesmo sinal, ou são ambas positivas (\(1ºQ\)) ou ambas negativas (\(4ºQ\)). Já no \(2º\) e \(3º\) quadrantes as coordenadas têm sinais diferentes, no \(2ºQ\) as abcissas são negativas e as ordenadas positivas já no \(3ºQ\) é o contrário. |
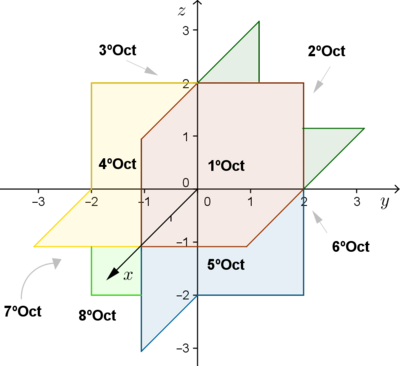
O espaço é também dividido em partes pelos eixos coordenados, às quais chamamos de octantes, existem assim oito octantes. A figura 5 ilustra essa divisão.
O sinal das coordenadas dos pontos em cada um dos octantes pode ser resumido na seguinte tabela:
| Octante | \((x,y,z)\) |
|---|---|
| \(1º\) | \((+,+,+)\) |
| \(2º\) | \((-,+,+)\) |
| \(3º\) | \((-,-,+)\) |
| \(4º\) | \((+,-,+)\) |
| \(5º\) | \((+,+,-)\) |
| \(6º\) | \((-,+,-)\) |
| \(7º\) | \((-,-,-)\) |
| \(8º\) | \((+,-,-)\) |
Referências
\([1]\) BARUK, Stella, Dictionnaire de Mathemátiques Elémentaires, 1992, Editions du Seuil, traduzido por SILVA, Maria do Céu, MIRRA, Maria Elisa, RIBEIRO, Maria de Fátima, 2005, Edições Afrontamento.
Criada em 30 de Janeiro de 2013
Revista em 19 de Fevereiro de 2013
Aceite pelo editor em 30 de Junho de 2017