Diferenças entre edições de "Acontecimentos independentes"

Da WikiCiências
Share/Save/Bookmark
Ir para: navegação, pesquisa
(Criou nova página com '<span style="font-size:8pt"><b>Referência : </b><font color="#003600" >Não citável</font></span> <span style="font-size:8pt"><font color="red">'''''Esta página ainda n…')
 
 
(64 edições intermédias de 3 utilizadores não apresentadas)
Linha 1: Linha 1:
−
<span style="font-size:8pt"><b>Referência : </b><font color="#003600" >Não citável</font></span>  <span style="font-size:8pt"><font color="red">'''''Esta página ainda não foi aprovada.'''''</font></span>
+
<span style="font-size:8pt"><b>Referência : </b> Martins, EGM, (2017) ''Acontecimentos independentes'', [http://rce.casadasciencias.org Rev. Ciência Elem.], V5(4):049
 
<br>
 
<br>
−
<span style="font-size:8pt"><b>Autor</b>: <i>Maria Eugénia Graça Martins</i></span><br>
+
<span style="font-size:8pt"><b>Autores</b>: <i>[[Usuário:Megm|Maria Eugénia Graça Martins]]</i> </span><br> <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usu&aacute;rio:Jfgomes47|José Ferreira Gomes]]</i></span><br>
−
<span style="font-size:8pt"><b>Editor</b>: <i>Colocar nome do editor</i></span>
+
<b>DOI</b>: <i>[[http://doi.org/10.24927/rce2017.049 http://doi.org/10.24927/rce2017.049]]</i></span><br>
−
 
+
<html><a href="https://rce.casadasciencias.org/rceapp/pdf/2017/049/" target="_blank">
 +
                <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html>
 
----
 
----
−
----
 
−
Dados os acontecimentos A e B, com P(B)\(\rm{>}0\), diz-se que o acontecimento A é independente do acontecimento B, se a probabilidade de A se verificar é igual à [[Probabilidade condicional|probabilidade condicional]] de A se verificar, dado que B se verificou
 
  
−
<div style="text-align: center;">
+
=Resumo=
−
/[P(A) = P(A|B)\]
+
De uma forma intuitiva somos levados a dizer que dois acontecimentos são independentes quando a realização de um deles não tem influência na realização do outro. Como avaliar esta influência? A Probabilidade condicional, um dos conceitos mais importantes da teoria da Probabilidade vai-nos permitir avaliar se, dados dois acontecimentos, a ocorrência de um deles condiciona, de alguma forma, a probabilidade de ocorrência do outro, conduzindo-nos, assim, à noção de independência entre acontecimentos.
−
</div>
+
 
 +
 
 +
<html>
 +
<p class='mainText'>Dados os acontecimentos A e B, com P(B)>0, diz-se que o acontecimento A é
 +
        <strong>independente</strong> do
 +
        acontecimento B, se a probabilidade de A se verificar é igual à probabilidade condicional de A se verificar,
 +
        dado que B se verificou</p>
 +
    <br>
 +
 
 +
    <center>P(A)=P(A|B)</center>
 +
    <br>
 +
 
 +
    <p class='mainText'>ou seja, o facto de se saber que o acontecimento B se realizou, não altera a probabilidade de A
 +
        se realizar.</p>
 +
    <p class='mainText'>Se o acontecimento A é <strong>independente</strong> do acontecimento B, então o acontecimento B
 +
        é <strong>independente</strong>
 +
        de A, se P(A)>0. Efetivamente, tendo em consideração a definição de probabilidade condicional, tem-se </p>
 +
    <br>
 +
    <center>P(B|A) \(=\frac{P(A∩B)}{P(A)}=\frac{P(B)P(A|B)}{P(A)}=\frac{P(B)P(A)}{P(A)}=\) P(B)</center>
 +
    <br>
 +
 
 +
    <p class='mainText'>Assim, os acontecimentos A e B, com P(A)xP(B)>0, são <strong>independentes</strong> quando a
 +
        ocorrência de um deles não altera a probabilidade da ocorrência do outro, ou seja:</p>
 +
    <br>
 +
 
 +
    <center>P(A|B)=P(A) e P(B|A)=P(B)</center>
 +
    <br>
 +
    <p class='mainText'>Repare-se que se alguma das condições anteriores se verifica, da definição de probabilidade
 +
        condicional vem que</p>
 +
    <br>
 +
    <center>P(A∩B)=P(A)xP(B)</center>
 +
    <br>
 +
    <p class='mainText'>A igualdade anterior costuma ser utilizada para definir a independência entre acontecimentos,
 +
        dizendo-se que:</p>
 +
    <p class='mainText'>Dois acontecimentos A e B são <strong>independentes</strong> se e só se </p>
 +
    <br>
 +
    <center>P(A∩B)=P(A)xP(B)</center>
 +
    <br>
 +
    <p class='mainText'>Esta definição de independência, embora não seja tão intuitiva, é a que é utilizada de um modo
 +
        geral, não sendo necessário impor restrições aos valores de P(A) e P(B). Por exemplo se P(A)=0, como A∩B⊆A, vem
 +
        P(A∩B)≤P(A) e A é independente de qualquer outro acontecimento.</p>
 +
    <p class='mainText'>As duas definições de independência são equivalentes desde que se exija que P(A)xP(B)>0.
 +
    </p>
 +
    <p class='mainText'>Exemplo – Considere-se uma caixa que contém 6 fichas de duas cores diferentes, numeradas de 1 a
 +
        3, conforme a figura junta:</p>
 +
    <br>
 +
    <figure class="image-small">
 +
        <center><img src="http://rce.casadasciencias.org/rceapp/static/images/articles/2017-049-01.jpg"></center>
 +
        <figcaption>
 +
        </figcaption>
 +
    </figure>
 +
    <br>
 +
    <p class='mainText'>Retira-se, ao acaso, uma ficha da caixa.</p>
 +
    <ol type="a">
 +
        <li style="list-style-type: lower-alpha">Qual a probabilidade de que seja uma ficha com o número 2?
 +
            Uma vez que temos 6 fichas, das quais 2 têm o número 2, P(2)=P(retirar ficha com 2)=2/6=1/3
 +
        </li>
 +
        <li style="list-style-type: lower-alpha">Depois de retirar a ficha, verificou que era verde. Qual a
 +
            probabilidade de que tenha o número 2? Os
 +
            acontecimentos Número da ficha e Cor serão independentes? </br>
 +
            Como agora temos a informação que a ficha é verde, pretende-se a probabilidade condicional de obter um 2,
 +
            sabendo que a ficha é verde, ou seja, P(2|cor verde)= \(\frac{P(cor\, verde\, e\, ter\, o\, 2)}{P(cor\,
 +
            verde)}=\frac{1/6}{3/6}=\frac{1}{3}\)</br>
 +
            Então, P(2|cor verde)=P(2)</br>
 +
            Se tivéssemos considerado qualquer dos outros números das fichas ou a cor amarela, obteríamos os mesmos
 +
            resultados, ou seja,</br>
 +
            <center>P(i|cor x)=P(i) para i=1, 2, 3 e x=amarela, verde</center>
 +
            <p>donde concluímos que os acontecimentos Número da ficha e Cor são independentes.</p>
 +
 
 +
        </li>
 +
    </ol>
 +
    <br>
 +
    <p class='mainText'>Suponha agora que alterou a composição da caixa, de forma que agora tem 2 fichas verdes,
 +
        numeradas de 1 a 2 e 4 fichas amarelas, numeradas de 1 a 4:</p>
 +
    <br>
 +
    <figure class="image-small">
 +
        <center><img src="http://rce.casadasciencias.org/rceapp//static/images/articles/2017-049-02.jpg"></center>
 +
        <figcaption>
 +
        </figcaption>
 +
    </figure>
 +
    <br>
 +
    <p class='mainText'>Retira-se, ao acaso, uma ficha da caixa.</p>
 +
    <br>
 +
    <ol type="a">
 +
        <li style="list-style-type: lower-alpha">Qual a probabilidade de que seja uma ficha com o número 2?
 +
            Uma vez que temos 6 fichas, das quais 2 têm o número 2, P(2)=P=2/6=1/3
 +
        </li>
 +
        <li style="list-style-type: lower-alpha">Depois de retirar a ficha, verificou que era verde. Qual a
 +
            probabilidade de que tenha o número 2? Pensa que esta probabilidade é igual à calculada na alínea anterior?
 +
            Os acontecimentos <em>Número da ficha</em> e <em>Cor</em> serão independentes?</br>
 +
            Como agora temos a informação que a ficha é verde, pretende-se a proba- bilidade condicional de obter um 2,
 +
            sabendo que a ficha é verde, ou
 +
            seja, P(2|cor verde)= \(\frac{P(cor\, verde\, e\, ter\, o\, 2)}{P(cor\,
 +
            verde)}=\frac{1/6}{2/6}=\frac{1}{2}\)</br>
 +
            Repare-se que agora a informação adicional de que a ficha é verde, aumentou a probabilidade de a ficha ter o
 +
            número 2. Agora os acontecimentos já não são independentes, pois P(2|cor verde)≠ P(2)
 +
 
 +
        </li>
 +
    </ol>
 +
    <br>
 +
    <p class='mainText'>A independência de acontecimentos é uma propriedade que depende do modelo de Probabilidade que
 +
        se introduziu no espaço de resultados, não sendo, portanto, uma propriedade dos acontecimentos. Consideremos o
 +
        seguinte exemplo, adaptado de <em>MURTEIRA ET AL</em> (2012), página 82:</p>
 +
    <p class='mainText'>Dada uma moeda de um euro, não necessariamente “equilibrada” em que representamos por E a face
 +
        Euro e N a face Nacional, consideremos o seguinte <em>modelo de probabilidade</em> para o fenómeno aleatório que
 +
        consiste
 +
        em verificar qual a face que fica voltada para cima após um lançamento da moeda</p>
 +
    <br>
 +
    <table style="width:100%" border="1">
 +
        <tr>
 +
            <td>Resultado
 +
            </td>
 +
            <td>E</td>
 +
            <td>N</td>
 +
        </tr>
 +
        <tr>
 +
            <td>Probabilidade</td>
 +
            <td>p</td>
 +
            <td>1-p</td>
 +
        </tr>
 +
    </table>
 +
    <br>
 +
    <p class='mainText'>com 0 ≤ p ≤ 1.</p>
 +
    <p class='mainText'>Considerem-se os acontecimentos</p>
 +
    <br>
 +
    <center>A={EEE, EEN, ENE, NEE} e B={EEE, NNN}</center>
 +
    <br>
 +
    <p class='mainText'>associados com três lançamentos independentes da moeda. Como</p>
 +
    <br>
 +
    <center>P(EEE) = P(E)P(E)P(E) =p<sup>3</sup>, P(EEN) = P(E)P(E)P(N) = p<sup>2</sup> (1-p),
 +
        etc.,
 +
        tem-se P(A) = p<sup>3</sup> + 3p<sup>3</sup> (1-p) e P(B) = p<sup>3</sup> + (1-p)<sup>3</sup></center>
 +
    <br>
 +
    <p class='mainText'>Pode-se mostrar que a igualdade P(A∩B)=P(A)P(B) só se verifica nos casos triviais p=0, p=1, e no
 +
        caso simétrico, p=1/2. Assim, A e B podem ser ou não independentes, consoante a natureza da moeda, ou seja do
 +
        valor de p que tenhamos considerado para o modelo de probabilidade anteriormente considerado.</p>
 +
    <br>
 +
    <p class='mainText'>Nota 1 – Dois acontecimentos não podem ser disjuntos (ou incompatíveis ou mutuamente exclusivos)
 +
        e independentes, a não ser que um deles tenha probabilidade nula. Efetivamente se os acontecimentos A e B, com
 +
        P(A)>0 e P(B)>0, são incompatíveis, não podem ser independentes, uma vez que P(A∩B)=P(∅)=0 e P(A)xP(B)>0, vindo
 +
        P(A∩B)≠P(A)xP(B).</p>
 +
 
 +
    <p class='mainText'>Nota 2 – É frequente fazer-se confusão com os conceitos de acontecimentos independentes e
 +
        acontecimentos incompatíveis. No entanto estes conceitos exprimem relações completamente diferentes, na medida
 +
        em que a incompatibilidade de acontecimentos é uma propriedade inerente aos acontecimentos, não sendo necessário
 +
        ter definido nenhuma probabilidade, enquanto que a independência de acontecimentos depende do modelo de
 +
        probabilidade que se tenha definido no espaço de resultados onde estão definidos os acontecimentos.</p>
 +
</html>
 +
 
 +
==Referências==
 +
MURTEIRA, B. e ANTUNES, M., Probabilidades e Estatística, volume I., ISBN 978-972-592-355-9, Escolar Editora, 2012.
 +
 
 +
----
  
 +
Recursos relacionados disponíveis na [http://www.casadasciencias.org Casa das Ciências]:<br>
 +
# [https://www.casadasciencias.org/recurso/8536 Probabilidades. Estatística e Ciência Experimental, por José Sebastião e Silva].<br>
  
 +
---- <br>Criada em 6 de Dezembro de 2017<br> Revista em 6 de Dezembro de 2017<br> Aceite pelo editor em 6 de Dezembro de 2017<br>
 
[[Category:Matemática]]
 
[[Category:Matemática]]

Edição actual desde as 15h42min de 19 de outubro de 2020

Referência : Martins, EGM, (2017) Acontecimentos independentes, Rev. Ciência Elem., V5(4):049
Autores: Maria Eugénia Graça Martins
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2017.049]
PDF Download

Resumo

De uma forma intuitiva somos levados a dizer que dois acontecimentos são independentes quando a realização de um deles não tem influência na realização do outro. Como avaliar esta influência? A Probabilidade condicional, um dos conceitos mais importantes da teoria da Probabilidade vai-nos permitir avaliar se, dados dois acontecimentos, a ocorrência de um deles condiciona, de alguma forma, a probabilidade de ocorrência do outro, conduzindo-nos, assim, à noção de independência entre acontecimentos.


Dados os acontecimentos A e B, com P(B)>0, diz-se que o acontecimento A é independente do acontecimento B, se a probabilidade de A se verificar é igual à probabilidade condicional de A se verificar, dado que B se verificou


P(A)=P(A|B)

ou seja, o facto de se saber que o acontecimento B se realizou, não altera a probabilidade de A se realizar.

Se o acontecimento A é independente do acontecimento B, então o acontecimento B é independente de A, se P(A)>0. Efetivamente, tendo em consideração a definição de probabilidade condicional, tem-se


P(B|A) \(=\frac{P(A∩B)}{P(A)}=\frac{P(B)P(A|B)}{P(A)}=\frac{P(B)P(A)}{P(A)}=\) P(B)

Assim, os acontecimentos A e B, com P(A)xP(B)>0, são independentes quando a ocorrência de um deles não altera a probabilidade da ocorrência do outro, ou seja:


P(A|B)=P(A) e P(B|A)=P(B)

Repare-se que se alguma das condições anteriores se verifica, da definição de probabilidade condicional vem que


P(A∩B)=P(A)xP(B)

A igualdade anterior costuma ser utilizada para definir a independência entre acontecimentos, dizendo-se que:

Dois acontecimentos A e B são independentes se e só se


P(A∩B)=P(A)xP(B)

Esta definição de independência, embora não seja tão intuitiva, é a que é utilizada de um modo geral, não sendo necessário impor restrições aos valores de P(A) e P(B). Por exemplo se P(A)=0, como A∩B⊆A, vem P(A∩B)≤P(A) e A é independente de qualquer outro acontecimento.

As duas definições de independência são equivalentes desde que se exija que P(A)xP(B)>0.

Exemplo – Considere-se uma caixa que contém 6 fichas de duas cores diferentes, numeradas de 1 a 3, conforme a figura junta:



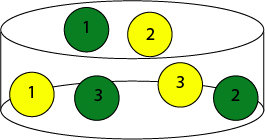
Retira-se, ao acaso, uma ficha da caixa.

  1. Qual a probabilidade de que seja uma ficha com o número 2? Uma vez que temos 6 fichas, das quais 2 têm o número 2, P(2)=P(retirar ficha com 2)=2/6=1/3
  2. Depois de retirar a ficha, verificou que era verde. Qual a probabilidade de que tenha o número 2? Os acontecimentos Número da ficha e Cor serão independentes?
    Como agora temos a informação que a ficha é verde, pretende-se a probabilidade condicional de obter um 2, sabendo que a ficha é verde, ou seja, P(2|cor verde)= \(\frac{P(cor\, verde\, e\, ter\, o\, 2)}{P(cor\, verde)}=\frac{1/6}{3/6}=\frac{1}{3}\)
    Então, P(2|cor verde)=P(2)
    Se tivéssemos considerado qualquer dos outros números das fichas ou a cor amarela, obteríamos os mesmos resultados, ou seja,
    P(i|cor x)=P(i) para i=1, 2, 3 e x=amarela, verde

    donde concluímos que os acontecimentos Número da ficha e Cor são independentes.


Suponha agora que alterou a composição da caixa, de forma que agora tem 2 fichas verdes, numeradas de 1 a 2 e 4 fichas amarelas, numeradas de 1 a 4:



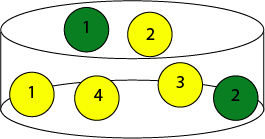
Retira-se, ao acaso, uma ficha da caixa.


  1. Qual a probabilidade de que seja uma ficha com o número 2? Uma vez que temos 6 fichas, das quais 2 têm o número 2, P(2)=P=2/6=1/3
  2. Depois de retirar a ficha, verificou que era verde. Qual a probabilidade de que tenha o número 2? Pensa que esta probabilidade é igual à calculada na alínea anterior? Os acontecimentos Número da ficha e Cor serão independentes?
    Como agora temos a informação que a ficha é verde, pretende-se a proba- bilidade condicional de obter um 2, sabendo que a ficha é verde, ou seja, P(2|cor verde)= \(\frac{P(cor\, verde\, e\, ter\, o\, 2)}{P(cor\, verde)}=\frac{1/6}{2/6}=\frac{1}{2}\)
    Repare-se que agora a informação adicional de que a ficha é verde, aumentou a probabilidade de a ficha ter o número 2. Agora os acontecimentos já não são independentes, pois P(2|cor verde)≠ P(2)

A independência de acontecimentos é uma propriedade que depende do modelo de Probabilidade que se introduziu no espaço de resultados, não sendo, portanto, uma propriedade dos acontecimentos. Consideremos o seguinte exemplo, adaptado de MURTEIRA ET AL (2012), página 82:

Dada uma moeda de um euro, não necessariamente “equilibrada” em que representamos por E a face Euro e N a face Nacional, consideremos o seguinte modelo de probabilidade para o fenómeno aleatório que consiste em verificar qual a face que fica voltada para cima após um lançamento da moeda


Resultado E N
Probabilidade p 1-p

com 0 ≤ p ≤ 1.

Considerem-se os acontecimentos


A={EEE, EEN, ENE, NEE} e B={EEE, NNN}

associados com três lançamentos independentes da moeda. Como


P(EEE) = P(E)P(E)P(E) =p3, P(EEN) = P(E)P(E)P(N) = p2 (1-p), etc., tem-se P(A) = p3 + 3p3 (1-p) e P(B) = p3 + (1-p)3

Pode-se mostrar que a igualdade P(A∩B)=P(A)P(B) só se verifica nos casos triviais p=0, p=1, e no caso simétrico, p=1/2. Assim, A e B podem ser ou não independentes, consoante a natureza da moeda, ou seja do valor de p que tenhamos considerado para o modelo de probabilidade anteriormente considerado.


Nota 1 – Dois acontecimentos não podem ser disjuntos (ou incompatíveis ou mutuamente exclusivos) e independentes, a não ser que um deles tenha probabilidade nula. Efetivamente se os acontecimentos A e B, com P(A)>0 e P(B)>0, são incompatíveis, não podem ser independentes, uma vez que P(A∩B)=P(∅)=0 e P(A)xP(B)>0, vindo P(A∩B)≠P(A)xP(B).

Nota 2 – É frequente fazer-se confusão com os conceitos de acontecimentos independentes e acontecimentos incompatíveis. No entanto estes conceitos exprimem relações completamente diferentes, na medida em que a incompatibilidade de acontecimentos é uma propriedade inerente aos acontecimentos, não sendo necessário ter definido nenhuma probabilidade, enquanto que a independência de acontecimentos depende do modelo de probabilidade que se tenha definido no espaço de resultados onde estão definidos os acontecimentos.

Referências

MURTEIRA, B. e ANTUNES, M., Probabilidades e Estatística, volume I., ISBN 978-972-592-355-9, Escolar Editora, 2012.

Recursos relacionados disponíveis na Casa das Ciências:

  1. Probabilidades. Estatística e Ciência Experimental, por José Sebastião e Silva.

Criada em 6 de Dezembro de 2017
Revista em 6 de Dezembro de 2017
Aceite pelo editor em 6 de Dezembro de 2017
Obtida de "https://wikiciencias.casadasciencias.org/wiki/index.php?title=Acontecimentos_independentes&oldid=29270"