Diferenças entre edições de "Equações da reta"
| (134 edições intermédias de 2 utilizadores não apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | <span style="font-size:8pt"><b>Referência : </b> | + | <span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) '' Equações da reta'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(2):074 |
<br> | <br> | ||
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | <span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | ||
| − | <span style="font-size:8pt"><b>Editor</b>: <i> | + | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Jfgomes47|José Ferreira Gomes]]</i></span><br> |
| − | + | <span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.074 https://doi.org/10.24927/rce2017.074]]</i></span><br> | |
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-074.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
---- | ---- | ||
| Linha 9: | Linha 11: | ||
__TOC__ | __TOC__ | ||
| − | =Reta | + | =Reta que passa num ponto e é perpendicular a um vetor= |
==Equação cartesiana== | ==Equação cartesiana== | ||
| − | |||
| − | + | {| border="0" | |
| + | |- | ||
| + | | Considerando um ponto \(A=(x_A,y_A)\) e um vetor \(\vec {\bf n}\), a reta que passa por \(A\) e é perpendicular a \(\vec {\bf n}\) é definida através da equação \(\vec {\bf n} \cdot \overrightarrow{AP}=0\), onde \(P=(x,y)\) um ponto genérico da reta considerada. | ||
| + | Se \( \vec {\bf n}=(a,b)\) e \(\overrightarrow{AP}=(x-x_A,y-y_A)\), \(\vec {\bf n} \cdot \overrightarrow{AP}=(a,b) \cdot (x-x_A,y-y_A)=a(x-x_A)+b(y-y_A)\), e então a equação escreve-se da forma, | ||
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[ | + | ! style="background: #efefef;" | \[\quad a(x-x_A) + b(y-y_A)=0 \quad\] |
|} | |} | ||
| − | + | e diz-se a <span style="color:red">'''equação cartesiana'''</span> <u>da reta</u> referida. | |
| − | + | <span style="color:#4682B4">'''''Exemplos'''''</span> | |
| − | + | ||
| − | + | * \(2x-y=0\) é a equação cartesiana da reta que passa, por exemplo, no ponto \(A=(1,2)\) e é perpendicular ao vetor \(\vec {\bf n} =(2,-1)\). | |
| − | + | * \(\displaystyle 2y=\frac{x}{3}\) é a equação cartesiana da reta que passa, por exemplo, no ponto \(A=(3,1/2)\) e é perpendicular ao vetor \(\vec {\bf n} =(-1/3,2)\). | |
| + | |||
| + | | | ||
| + | |<html><iframe scrolling="no" title="Equações da reta" src="https://www.geogebra.org/material/iframe/id/pejcsdu4/width/400/height/350/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="400px" height="350px" style="border:0px;"> </iframe></html> | ||
|} | |} | ||
| − | |||
| + | <span style="color:#4682B4">'''''Aplicação'''''</span> | ||
| − | + | Como calcular a equação cartesiana da reta que passa em \(A=(-1,2)\) e é perpendicular ao vetor \(\vec {\bf n}=(3,4)\)? | |
| − | + | Consideramos \(P=(x,y)\) um ponto genérico dessa reta, então o vetor \(\overrightarrow{AP}=P-A=(x,y)-(-1,2)=(x+1,y-2)\) é ortogonal ao vetor \(\vec {\bf n}\). Portanto, \(\overrightarrow{AP} \cdot \vec {\bf n}=0\), isto é, | |
| − | + | ||
| − | + | \((x+1,y-2) \cdot (3,4)=0 \, \Leftrightarrow \, 3(x+1)+4(y-2)=0 \, \Leftrightarrow \, 3x+4y=5\). | |
==Equação vetorial== | ==Equação vetorial== | ||
| − | + | {| class="wikitable" | |
| − | Considerando a mesma reta, \(\vec | + | |- |
| + | | Considerando a mesma reta, \(\vec {\bf n} \cdot \overrightarrow{AP} =0\), onde \(\vec {\bf n}=(a,b)\), vejamos que o vetor \(\vec {\bf v}=(-b,a)\) tem a mesma direção dessa reta. De facto \(\vec {\bf n} \cdot \vec {\bf v}=(a,b) \cdot (-b,a)= -ab+ba=0\). Portanto a reta é também o conjunto de todos os pontos \(P=(x,y)\), tais que \(P-A=\overrightarrow{AP}\) é um múltiplo escalar de vetor \(\vec {\bf v}\). Isto é, \((P-A)=t \vec {\bf v}\). | ||
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
| − | |- | + | |- |
| − | + | ! style="background: #efefef;" | \[\quad P \in \mathbb{R}^2: P=A+t\vec {\bf v} , \quad t \in \mathbb{R} \quad\] | |
| − | ! style="background: #efefef;" | \[\ | + | |
|} | |} | ||
| − | A equação \( | + | A equação \(P=A+t\vec {\bf v}\) diz-se a <span style="color:red">'''equação vetorial'''</span> da reta que passa no ponto \(A\) e é paralela ao vetor \(\vec {\bf v}\). |
| + | | | ||
| + | |<html><iframe scrolling="no" title="Equações da reta" src="https://www.geogebra.org/material/iframe/id/d9kwdmbq/width/420/height/250/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="420px" height="250px" style="border:0px;"> </iframe></html> | ||
| + | |} | ||
==Equações paramétricas== | ==Equações paramétricas== | ||
| − | Se \(\ | + | {| border="0" |
| + | |- | ||
| + | | Se \( \overrightarrow{AP} =(x-x_A,y-y_A)\), então, como \(\vec{\bf v}=(-b,a)\), | ||
| + | \(\overrightarrow{AP}=t \vec {\bf v} \, \Leftrightarrow \, (x-x_A,y-y_A)=t(-b,a) \, \Leftrightarrow \, x-x_A=-tb \wedge y-y_A=ta\), sendo assim equivalente ao sistema de duas equações seguinte: | ||
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[ \left\{\begin{array}{ll} x=-tb & \\ & , t \in \mathbb{R} \\ y=ta & \end{array} \right.\] | + | | ! style="background: #efefef;" | \[ \quad \left\{\begin{array}{ll} x=x_A-tb & \\ & , t \in \mathbb{R} \\ y=y_A+ ta & \end{array} \right.\quad \] |
|} | |} | ||
Que se dizem <span style="color:red">'''equações paramétricas'''</span> da reta referida. | Que se dizem <span style="color:red">'''equações paramétricas'''</span> da reta referida. | ||
| − | Quando o "tempo" \(t\) varia, elas representam o movimento de um ponto (partícula) que se desloca sobre a reta com movimento uniforme de vetor-velocidade \(\vec v=(-b,a)\) e velocidade (escalar) \(v=\|\vec v\|=\sqrt{a^2+b^2}\). | + | Quando o "tempo" \(t\) varia, elas representam o movimento de um ponto (partícula) que se desloca sobre a reta com movimento uniforme de vetor-velocidade \(\vec {\bf v}=(-b,a)\) e velocidade (escalar) \(v=\|\vec {\bf v}\|=\sqrt{a^2+b^2}\). |
| + | | | ||
| + | | <span style="color:#4682B4">'''''Aplicação'''''</span> | ||
| − | + | Como calcular as equações paramétricas da reta que passa no ponto \(A=(2,-3)\) e é perpendicular ao vetor \(\vec {\bf n}=(1,4)\)? | |
| + | O vetor \(\vec {\bf v}=(-4,1)\) é perpendicular ao vetor \(\vec {\bf n}\) pois \(\vec {\bf n} \cdot \vec {\bf v}=(1,4) \cdot (-4,1)=-4+4=0\). Portanto, pretendemos as equações paramétricas da reta que passa em \(A=(2,-3)\) e é paralela ao vetor \(\vec {\bf v}=(-4,1)\). Se \(P=(x,y)\) um ponto genérico dessa reta, então \(\overrightarrow{AP}=P-A=(x,y)-(2,-3)=(x-2,y+3)\) é um múltiplo escalar do vetor \(\vec {\bf v}\), isto é, \(\overrightarrow{AP}=t\vec {\bf v}\), ou seja, | ||
| + | |||
| + | \((x-2,y+3)=t(-4,1) \, \Longleftrightarrow \, \left\{\begin{array}{ll} x=2-4t \\ y=-3+t \, , \quad t \in \mathbb{R}\end{array}\right.\) | ||
| + | |} | ||
| + | |||
| + | <div style="text-align: center;"> | ||
| + | <html><iframe scrolling="no" title="Equações da reta" src="https://www.geogebra.org/material/iframe/id/zxfbn8yh/width/350/height/250/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="350px" height="250px" style="border:0px;"> </iframe></html> | ||
| + | </div> | ||
=Reta que passa por dois pontos= | =Reta que passa por dois pontos= | ||
| Linha 70: | Linha 93: | ||
==Equação vetorial== | ==Equação vetorial== | ||
| − | Pretendemos agora determinar a equação de uma reta que passa em dois pontos distintos. Temos então dois casos | + | {| border="0" |
| + | |- | ||
| + | |Pretendemos agora determinar a equação de uma reta que passa em dois pontos distintos. Temos então dois casos: | ||
| − | No plano, sejam \(A=(x_A,y_A)\) e \(B=(x_B,y_B)\) esses dois pontos, queremos então determinar a equação da reta que passa por \(A\) e é paralela ao vetor \(\overrightarrow{AB}\). Se \(P=(x,y)\) é um ponto genérico dessa | + | <u>No plano</u>, sejam \(A=(x_A,y_A)\) e \(B=(x_B,y_B)\) esses dois pontos, queremos então determinar a equação da reta que passa por \(A\) e é paralela ao vetor \(\overrightarrow{AB}\). Se \(P=(x,y)\) é um ponto genérico dessa reta temos que, |
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[P=A+t\overrightarrow{AB}\, , \quad t \in \mathbb{R}\] | + | ! style="background: #efefef;" | \[\quad P=A+t\overrightarrow{AB}\, , \quad t \in \mathbb{R}\quad \] |
|} | |} | ||
que é chamada a <span style="color:red">'''equação vetorial'''</span> da reta. Em coordenadas, \((x,y)=(x_A,y_A)+t(x_B-x_A,y_B-y_A) \, , \quad t \in \mathbb{R}\). | que é chamada a <span style="color:red">'''equação vetorial'''</span> da reta. Em coordenadas, \((x,y)=(x_A,y_A)+t(x_B-x_A,y_B-y_A) \, , \quad t \in \mathbb{R}\). | ||
| + | |||
| + | <u>No espaço</u>, considerando \(A=(x_A,y_A,z_A)\) e \(B=(x_B,y_B,z_B)\) os dois pontos pelos quais passa a reta a sua '''equação vetorial''' é: | ||
| + | |||
| + | \[(x,y,z)=(x_A,y_A,z_A)+t(x_B-x_A,y_B-y_A,z_B-z_A) \, , \quad t \in \mathbb{R}\]. | ||
| + | | | ||
| + | | <span style="color:#4682B4">'''''Aplicação'''''</span> | ||
| + | |||
| + | Como calcular a equação vetorial da reta que passa pelos pontos \(A=(2,-1,0)\) e \(B=(-3,1,2)\)? | ||
| + | |||
| + | Consideramos \(P=(x,y,z)\) um ponto genérico dessa reta. A reta pretendida passa pelos pontos \(A\) e \(B\) por isso é uma reta paralela ao vetor \(\overrightarrow{AB}=B-A=(-3,1,2)-(2,-1,0)=(-5,0,2)\). Portanto a equação vetorial dessa reta é dada por: | ||
| + | |||
| + | \(P=A+t\overrightarrow{AB} \, \Longleftrightarrow \, (x,y,z)=(2,-1,0)+t(-5,0,2) \, , \quad t \in \mathbb{R}\) | ||
| + | |||
| + | [[Imagem: Eqvetorialpontos.png|thumb|center|450px|'''Fig.1''' - Reta que passa por dois pontos (no espaço)]] | ||
| + | |} | ||
==Equações paramétricas== | ==Equações paramétricas== | ||
| − | A equação vetorial | + | Das equações vetoriais da reta anteriores podemos obter as <span style="color:red">'''equações paramétricas'''</span>. |
| + | Para o caso em que \(A\) e \(B\) são pontos em \(\mathbb{R}^2\) a equação vetorial da reta é equivalente a \(x=x_A+t(x_b-x_A) \, \wedge \, y=y_A+t(y_B-y_A)\), ou num sistema: | ||
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[ \left\{\begin{array}{ll} x=x_A+t( | + | ! style="background: #efefef;" | \[ \quad \left\{\begin{array}{ll} x=x_A+t(x_B-x_A) & \\ & , t \in \mathbb{R} \\ y=y_A+t(y_B-y_A) & \end{array} \right. \quad\] |
|} | |} | ||
| − | + | ||
| + | Para o caso em que \(A\) e \(B\) são pontos em \(\mathbb{R}^3\) a equação vetorial da reta é equivalente a \(x=x_A+t(x_b-x_A) \, \wedge \, y=y_A+t(y_B-y_A) \, \wedge \, z=z_A+t(z_B-z_A)\), ou num sistema, considerando \(t \in \mathbb{R}\): | ||
| + | |||
| + | {| border="0" style="text-align: center;" align="center" | ||
| + | |- | ||
| + | ! style="background: #efefef;" | \[ \quad\left\{\begin{array}{l} x=x_A+t(x_B-x_A) \\ y=y_A+t(y_B-y_A) \\ z=z_A+t(z_B-z_A) \end{array} \right. \quad\] | ||
| + | |} | ||
==Equação cartesiana== | ==Equação cartesiana== | ||
| − | Simplificando | + | Simplificando os sistemas anteriores e eliminando o parâmetro \(t\), obtemos do primeiro sistema a <span style="color:red">'''equação cartesiana'''</span> da reta <u>no plano</u>, que passa pelos pontos \(A=(x_A,y_A)\) e \(B=(x_B,y_B)\): |
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[(y_B-y_A)(x-x_A)=(y-y_A)(x_B-x_A)\] | + | ! style="background: #efefef;" | \[\quad(y_B-y_A)(x-x_A)=(y-y_A)(x_B-x_A)\quad\] |
|} | |} | ||
| − | |||
* Se \(x_B-x_A=0\), então \(y_B-y_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta vertical de equação \(x=x_A\). | * Se \(x_B-x_A=0\), então \(y_B-y_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta vertical de equação \(x=x_A\). | ||
* Se \(y_B-y_A=0\), então \(x_B-x_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta horizontal de equação \(y=y_A\). | * Se \(y_B-y_A=0\), então \(x_B-x_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta horizontal de equação \(y=y_A\). | ||
* Se \(x_B-x_A \neq 0\) e \(y_B-y_A \neq 0\), a reta tem por equação: | * Se \(x_B-x_A \neq 0\) e \(y_B-y_A \neq 0\), a reta tem por equação: | ||
| + | |||
| + | \[y=y_A+\frac{(y_B-y_A)}{(x_B-x_A)}(x-x_A)\] | ||
| + | |||
| + | Do segundo sistema obtemos as '''equações cartesianas''' (também chamadas '''equações homogéneas''') da reta que passa em \(A\) e \(B\) <u>no espaço</u>, com \(A, B \in \mathbb{R}^3\). | ||
{| border="0" style="text-align: center;" align="center" | {| border="0" style="text-align: center;" align="center" | ||
|- | |- | ||
| − | ! style="background: #efefef;" | \[ | + | ! style="background: #efefef;" | \[\quad\frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-y_A}=\frac{z-z_A}{z_B-z_A}\quad\] |
|} | |} | ||
| − | + | ||
| − | + | =Equação reduzida de uma reta= | |
| + | |||
| + | ==Inclinação e declive da reta== | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | A '''inclinação''' de uma reta é o menor ângulo positivo \(\alpha\) que a reta faz com a parte positiva do eixo dos \(xx\). | ||
| + | |||
| + | Considerando dois pontos dessa reta, \(A(x_A,y_A)\) e \(B=(x_B,y_B)\), o '''declive''' da reta, usualmente denominado por \(m\), é o quociente entre a diferença das ordenadas e a diferença das abcissas de dois pontos dessa mesma reta, ou seja, | ||
| + | |||
| + | \[m=\frac{y_B-y_A}{x_B-x_A}\] | ||
| + | |||
| + | Se \(x_B-x_A \neq 0\) e \(y_B-y_A\neq 0\) então temos uma reta não vertical e não horizontal. Se \(x_B-x_A=0\) a reta é vertical e diz-se que o seu declive é infinito. Já se \(y_B-y_A=0\) temos uma reta horizontal (com declive nulo). | ||
| + | |||
| + | Através da trigonometria, o ''declive'' de uma reta é diretamente associado à inclinação da mesma pois, pela definição de tangente de um ângulo concluímos que o declive da reta é igual à tangente da inclinação da mesma, ou seja: | ||
| + | |||
| + | \[m=\tan \alpha\]. | ||
| + | || | ||
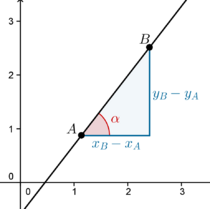
| + | [[Imagem: Eqreduzida2.png|thumb|upright|210px|'''Fig.2''' - Inclinação \(\alpha\) e declive de uma reta.]] | ||
| + | |} | ||
| + | |||
| + | ==Equação \(y=mx+b\)== | ||
| + | |||
| + | A equação reduzida de uma reta no plano é definida através da expressão, | ||
| + | |||
| + | \[y=mx+b\] | ||
| + | |||
| + | em que \(m\) é o declive da reta e \(b\) a ordenada na origem. | ||
| + | O valor \(b\) é assim a ordenada do ponto de interseção da reta considerada com o eixo dos \(yy\), ponto \((0,b)\), ou o valor que se obtém para \(y\) quando substituímos o valor de \(x\) por zero. | ||
| + | |||
| + | |||
| + | <span style="color:#4682B4">'''''Aplicação'''''</span> | ||
| + | |||
| + | Como calcular a equação reduzida da reta que passa pelos pontos \(A=(2,-1)\) e \(B=(4,6)\)? | ||
| + | |||
| + | Começamos por determinar o declive da reta: \(\displaystyle m=\frac{6-(-1)}{4-2} \, \Leftrightarrow \, m=\frac{7}{2}\). Temos então que \(\displaystyle y=\frac{7}{2}x+b\). | ||
| + | Para determinarmos o valor de \(b\) basta substituirmos na expressão anterior os valores de \(x\) e \(y\) pelas coordenadas de um dos pontos. Substituindo pelas coordenadas de \(A\) obtemos: | ||
| + | |||
| + | \(\displaystyle -1=\frac{7}{2}\times 2 +b \, \Leftrightarrow \, b=-1-7=-8\). | ||
| + | |||
| + | Concluímos então que a equação da reta pretendida é \(\displaystyle y=\frac{7}{2}x-8\). | ||
| + | |||
| + | |||
| + | ---- <br>Criada em 3 de Junho de 2013<br> Revista em 12 de Junho de 2013<br> Aceite pelo editor em 30 de Junho de 2017<br> | ||
[[Category:Matemática]] | [[Category:Matemática]] | ||
Edição actual desde as 08h45min de 13 de julho de 2021
Referência : Tavares, J., Geraldo, A., (2017) Equações da reta, Rev. Ciência Elem., V5(2):074
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.074]

Índice |
Reta que passa num ponto e é perpendicular a um vetor
Equação cartesiana
| Considerando um ponto \(A=(x_A,y_A)\) e um vetor \(\vec {\bf n}\), a reta que passa por \(A\) e é perpendicular a \(\vec {\bf n}\) é definida através da equação \(\vec {\bf n} \cdot \overrightarrow{AP}=0\), onde \(P=(x,y)\) um ponto genérico da reta considerada.
Se \( \vec {\bf n}=(a,b)\) e \(\overrightarrow{AP}=(x-x_A,y-y_A)\), \(\vec {\bf n} \cdot \overrightarrow{AP}=(a,b) \cdot (x-x_A,y-y_A)=a(x-x_A)+b(y-y_A)\), e então a equação escreve-se da forma,
e diz-se a equação cartesiana da reta referida.
|
Aplicação
Como calcular a equação cartesiana da reta que passa em \(A=(-1,2)\) e é perpendicular ao vetor \(\vec {\bf n}=(3,4)\)?
Consideramos \(P=(x,y)\) um ponto genérico dessa reta, então o vetor \(\overrightarrow{AP}=P-A=(x,y)-(-1,2)=(x+1,y-2)\) é ortogonal ao vetor \(\vec {\bf n}\). Portanto, \(\overrightarrow{AP} \cdot \vec {\bf n}=0\), isto é,
\((x+1,y-2) \cdot (3,4)=0 \, \Leftrightarrow \, 3(x+1)+4(y-2)=0 \, \Leftrightarrow \, 3x+4y=5\).
Equação vetorial
Considerando a mesma reta, \(\vec {\bf n} \cdot \overrightarrow{AP} =0\), onde \(\vec {\bf n}=(a,b)\), vejamos que o vetor \(\vec {\bf v}=(-b,a)\) tem a mesma direção dessa reta. De facto \(\vec {\bf n} \cdot \vec {\bf v}=(a,b) \cdot (-b,a)= -ab+ba=0\). Portanto a reta é também o conjunto de todos os pontos \(P=(x,y)\), tais que \(P-A=\overrightarrow{AP}\) é um múltiplo escalar de vetor \(\vec {\bf v}\). Isto é, \((P-A)=t \vec {\bf v}\).
A equação \(P=A+t\vec {\bf v}\) diz-se a equação vetorial da reta que passa no ponto \(A\) e é paralela ao vetor \(\vec {\bf v}\). |
Equações paramétricas
| Se \( \overrightarrow{AP} =(x-x_A,y-y_A)\), então, como \(\vec{\bf v}=(-b,a)\),
\(\overrightarrow{AP}=t \vec {\bf v} \, \Leftrightarrow \, (x-x_A,y-y_A)=t(-b,a) \, \Leftrightarrow \, x-x_A=-tb \wedge y-y_A=ta\), sendo assim equivalente ao sistema de duas equações seguinte:
Que se dizem equações paramétricas da reta referida. Quando o "tempo" \(t\) varia, elas representam o movimento de um ponto (partícula) que se desloca sobre a reta com movimento uniforme de vetor-velocidade \(\vec {\bf v}=(-b,a)\) e velocidade (escalar) \(v=\|\vec {\bf v}\|=\sqrt{a^2+b^2}\). |
Aplicação
Como calcular as equações paramétricas da reta que passa no ponto \(A=(2,-3)\) e é perpendicular ao vetor \(\vec {\bf n}=(1,4)\)? O vetor \(\vec {\bf v}=(-4,1)\) é perpendicular ao vetor \(\vec {\bf n}\) pois \(\vec {\bf n} \cdot \vec {\bf v}=(1,4) \cdot (-4,1)=-4+4=0\). Portanto, pretendemos as equações paramétricas da reta que passa em \(A=(2,-3)\) e é paralela ao vetor \(\vec {\bf v}=(-4,1)\). Se \(P=(x,y)\) um ponto genérico dessa reta, então \(\overrightarrow{AP}=P-A=(x,y)-(2,-3)=(x-2,y+3)\) é um múltiplo escalar do vetor \(\vec {\bf v}\), isto é, \(\overrightarrow{AP}=t\vec {\bf v}\), ou seja, \((x-2,y+3)=t(-4,1) \, \Longleftrightarrow \, \left\{\begin{array}{ll} x=2-4t \\ y=-3+t \, , \quad t \in \mathbb{R}\end{array}\right.\) |
Reta que passa por dois pontos
Equação vetorial
| Pretendemos agora determinar a equação de uma reta que passa em dois pontos distintos. Temos então dois casos:
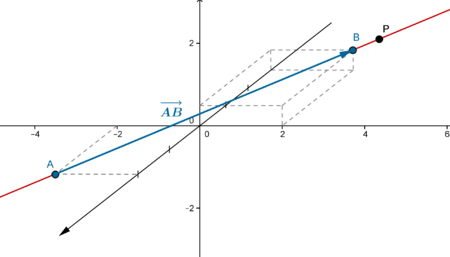
No plano, sejam \(A=(x_A,y_A)\) e \(B=(x_B,y_B)\) esses dois pontos, queremos então determinar a equação da reta que passa por \(A\) e é paralela ao vetor \(\overrightarrow{AB}\). Se \(P=(x,y)\) é um ponto genérico dessa reta temos que,
que é chamada a equação vetorial da reta. Em coordenadas, \((x,y)=(x_A,y_A)+t(x_B-x_A,y_B-y_A) \, , \quad t \in \mathbb{R}\).
\[(x,y,z)=(x_A,y_A,z_A)+t(x_B-x_A,y_B-y_A,z_B-z_A) \, , \quad t \in \mathbb{R}\]. |
Aplicação
Como calcular a equação vetorial da reta que passa pelos pontos \(A=(2,-1,0)\) e \(B=(-3,1,2)\)? Consideramos \(P=(x,y,z)\) um ponto genérico dessa reta. A reta pretendida passa pelos pontos \(A\) e \(B\) por isso é uma reta paralela ao vetor \(\overrightarrow{AB}=B-A=(-3,1,2)-(2,-1,0)=(-5,0,2)\). Portanto a equação vetorial dessa reta é dada por: \(P=A+t\overrightarrow{AB} \, \Longleftrightarrow \, (x,y,z)=(2,-1,0)+t(-5,0,2) \, , \quad t \in \mathbb{R}\) |
Equações paramétricas
Das equações vetoriais da reta anteriores podemos obter as equações paramétricas. Para o caso em que \(A\) e \(B\) são pontos em \(\mathbb{R}^2\) a equação vetorial da reta é equivalente a \(x=x_A+t(x_b-x_A) \, \wedge \, y=y_A+t(y_B-y_A)\), ou num sistema:
| \[ \quad \left\{\begin{array}{ll} x=x_A+t(x_B-x_A) & \\ & , t \in \mathbb{R} \\ y=y_A+t(y_B-y_A) & \end{array} \right. \quad\] |
|---|
Para o caso em que \(A\) e \(B\) são pontos em \(\mathbb{R}^3\) a equação vetorial da reta é equivalente a \(x=x_A+t(x_b-x_A) \, \wedge \, y=y_A+t(y_B-y_A) \, \wedge \, z=z_A+t(z_B-z_A)\), ou num sistema, considerando \(t \in \mathbb{R}\):
| \[ \quad\left\{\begin{array}{l} x=x_A+t(x_B-x_A) \\ y=y_A+t(y_B-y_A) \\ z=z_A+t(z_B-z_A) \end{array} \right. \quad\] |
|---|
Equação cartesiana
Simplificando os sistemas anteriores e eliminando o parâmetro \(t\), obtemos do primeiro sistema a equação cartesiana da reta no plano, que passa pelos pontos \(A=(x_A,y_A)\) e \(B=(x_B,y_B)\):
| \[\quad(y_B-y_A)(x-x_A)=(y-y_A)(x_B-x_A)\quad\] |
|---|
- Se \(x_B-x_A=0\), então \(y_B-y_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta vertical de equação \(x=x_A\).
- Se \(y_B-y_A=0\), então \(x_B-x_A \neq 0\), pois os dois pontos são distintos, e a reta é uma reta horizontal de equação \(y=y_A\).
- Se \(x_B-x_A \neq 0\) e \(y_B-y_A \neq 0\), a reta tem por equação:
\[y=y_A+\frac{(y_B-y_A)}{(x_B-x_A)}(x-x_A)\]
Do segundo sistema obtemos as equações cartesianas (também chamadas equações homogéneas) da reta que passa em \(A\) e \(B\) no espaço, com \(A, B \in \mathbb{R}^3\).
| \[\quad\frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-y_A}=\frac{z-z_A}{z_B-z_A}\quad\] |
|---|
Equação reduzida de uma reta
Inclinação e declive da reta
| A inclinação de uma reta é o menor ângulo positivo \(\alpha\) que a reta faz com a parte positiva do eixo dos \(xx\).
Considerando dois pontos dessa reta, \(A(x_A,y_A)\) e \(B=(x_B,y_B)\), o declive da reta, usualmente denominado por \(m\), é o quociente entre a diferença das ordenadas e a diferença das abcissas de dois pontos dessa mesma reta, ou seja, \[m=\frac{y_B-y_A}{x_B-x_A}\] Se \(x_B-x_A \neq 0\) e \(y_B-y_A\neq 0\) então temos uma reta não vertical e não horizontal. Se \(x_B-x_A=0\) a reta é vertical e diz-se que o seu declive é infinito. Já se \(y_B-y_A=0\) temos uma reta horizontal (com declive nulo). Através da trigonometria, o declive de uma reta é diretamente associado à inclinação da mesma pois, pela definição de tangente de um ângulo concluímos que o declive da reta é igual à tangente da inclinação da mesma, ou seja: \[m=\tan \alpha\]. |
Equação \(y=mx+b\)
A equação reduzida de uma reta no plano é definida através da expressão,
\[y=mx+b\]
em que \(m\) é o declive da reta e \(b\) a ordenada na origem. O valor \(b\) é assim a ordenada do ponto de interseção da reta considerada com o eixo dos \(yy\), ponto \((0,b)\), ou o valor que se obtém para \(y\) quando substituímos o valor de \(x\) por zero.
Aplicação
Como calcular a equação reduzida da reta que passa pelos pontos \(A=(2,-1)\) e \(B=(4,6)\)?
Começamos por determinar o declive da reta: \(\displaystyle m=\frac{6-(-1)}{4-2} \, \Leftrightarrow \, m=\frac{7}{2}\). Temos então que \(\displaystyle y=\frac{7}{2}x+b\). Para determinarmos o valor de \(b\) basta substituirmos na expressão anterior os valores de \(x\) e \(y\) pelas coordenadas de um dos pontos. Substituindo pelas coordenadas de \(A\) obtemos:
\(\displaystyle -1=\frac{7}{2}\times 2 +b \, \Leftrightarrow \, b=-1-7=-8\).
Concluímos então que a equação da reta pretendida é \(\displaystyle y=\frac{7}{2}x-8\).
Criada em 3 de Junho de 2013
Revista em 12 de Junho de 2013
Aceite pelo editor em 30 de Junho de 2017