Diferenças entre edições de "Inequações"
(→Inequações de 1º grau) |
|||
| (68 edições intermédias de um utilizador não apresentadas) | |||
| Linha 1: | Linha 1: | ||
| − | <span style="font-size:8pt"><b>Referência : </b> | + | <span style="font-size:8pt"><b>Referência : </b> Tavares, J., Geraldo, A., (2017) '' Inequações'', [https://rce.casadasciencias.org Rev. Ciência Elem.], V5(2):073 |
<br> | <br> | ||
<span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | <span style="font-size:8pt"><b>Autor</b>: <i>João Nuno Tavares e Ângela Geraldo</i></span><br> | ||
| − | <span style="font-size:8pt"><b>Editor</b>: <i> | + | <span style="font-size:8pt"><span style="font-size:8pt"><b>Editor</b>: <i>[[Usuário:Jfgomes47|José Ferreira Gomes]]</i></span><br> |
| + | <span style="font-size:8pt"><b>DOI</b>: <i>[[https://doi.org/10.24927/rce2017.073 https://doi.org/10.24927/rce2017.073]]</i></span><br> | ||
| + | <html><a href="https://rce.casadasciencias.org/rceapp/static/docs/artigos/2017-073.pdf" target="_blank"> | ||
| + | <img src="https://rce.casadasciencias.org/static/images/layout/pdf.png" alt="PDF Download"></a></html> | ||
---- | ---- | ||
==Definição== | ==Definição== | ||
| − | Uma '''inequação''' a uma incógnita é uma desigualdade que | + | Uma '''inequação''' em \(\mathbb{R}\) a uma incógnita é uma desigualdade que contem uma variável real. Assim, dá-se o nome de inequação a uma desigualdade à qual não se pode atribuir um valor de verdade (dizer se é verdadeira ou falsa), porque o seu valor de verdade depende do valor numérico que for atribuído à variável. |
| − | São <u>exemplos</u> de inequações: \(2x+3 > 10\), \(\quad 8-z \ge 11\). | + | São <u>exemplos</u> de inequações: \(2x+3 > 10\), \(\quad 8-z \ge 11\) e \(-2a^2+3 \le 7a\), onde \(x,z,a\in \mathbb{R}\). |
| − | Resolver uma inequação é determinar os conjuntos ou os intervalos de valores que se podem atribuir à variável de modo a tornar a desigualdade verdadeira. | + | Resolver uma inequação é determinar os conjuntos ou os intervalos de valores que se podem atribuir à variável de modo a tornar a desigualdade verdadeira. |
==Inequações de 1º grau== | ==Inequações de 1º grau== | ||
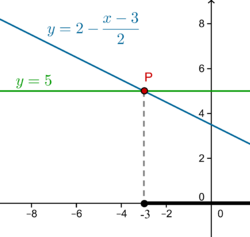
| − | A resolução de inequações do 1ºgrau comporta os | + | [[Ficheiro:Ineq1graua2.png|thumb|right|250px|'''Figura 1 -''' A função \(\displaystyle y=2-\frac{x-3}{2}\) tem imagem inferior ou igual a \(y=5\) a partir do ponto \(P\), ou seja para valores de \(x\) maiores ou iguais a \(-3\).]] |
| + | A resolução de inequações do 1ºgrau comporta os mesmos desafios e os mesmos procedimentos que a resolução de equações do 1ºgrau. Assim, o objetivo principal da resolução de inequações do 1ºgrau será isolar a incógnita num dos membros, ou seja, obter \(x> \dots\), \(\quad x < \dots\), \(\quad x \le \dots\) ou \(\quad x \ge \dots\). | ||
Na resolução destas inequações podemos utilizar as propriedades das desigualdades de forma a não modificar o seu valor de verdade. Para isso, podemos transformar a desigualdade por adição, subtração, multiplicação e divisão por um <u>número positivo</u> como fazemos na resolução de equações. No caso da multiplicação ou divisão por um <u>número negativo</u>, existe uma diferença essencial relativamente às equações, pois no caso das inequações será necessário alterar o sentido da desigualdade para manter o mesmo valor de verdade. | Na resolução destas inequações podemos utilizar as propriedades das desigualdades de forma a não modificar o seu valor de verdade. Para isso, podemos transformar a desigualdade por adição, subtração, multiplicação e divisão por um <u>número positivo</u> como fazemos na resolução de equações. No caso da multiplicação ou divisão por um <u>número negativo</u>, existe uma diferença essencial relativamente às equações, pois no caso das inequações será necessário alterar o sentido da desigualdade para manter o mesmo valor de verdade. | ||
Qualquer inequação do 1ºgrau, pode ser reduzida, através das operações referidas anteriormente, a uma das quatro formas seguintes: | Qualquer inequação do 1ºgrau, pode ser reduzida, através das operações referidas anteriormente, a uma das quatro formas seguintes: | ||
| − | \(ax < b\), \(\quad ax > b\), \(\quad ax \le b\) ou \(\quad ax \ge b\) | + | \(ax < b\), \(\quad ax > b\), \(\quad ax \le b \quad\) ou \(\quad ax \ge b\) |
podendo \(a\) ser positivo ou negativo mas nunca nulo. | podendo \(a\) ser positivo ou negativo mas nunca nulo. | ||
| Linha 31: | Linha 35: | ||
\(\displaystyle 2- \frac{x-3}{2} \le 5 \, \Longleftrightarrow \, 4-x+3 \le 10 \, \Longleftrightarrow \, -x \le 3 \, \Longleftrightarrow \, x \ge -3\) | \(\displaystyle 2- \frac{x-3}{2} \le 5 \, \Longleftrightarrow \, 4-x+3 \le 10 \, \Longleftrightarrow \, -x \le 3 \, \Longleftrightarrow \, x \ge -3\) | ||
| − | Logo o conjunto-solução desta inequação é \( | + | Logo o conjunto-solução desta inequação é \(\quad [-3, +\infty[ \), ver esquema figura 1. |
| + | |||
==Inequações de 2º grau== | ==Inequações de 2º grau== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Uma inequação do 2ºgrau (ou inequação quadrática) é uma inequação em que a incógnita toma grau dois num dos termos. Ou seja, é uma inequação do tipo | ||
| + | \(ax^2+bx+c \le 0\) | ||
| − | ==Inequações de funções racionais== | + | em que o sinal da desigualdade pode ser \(>, <, \le\) ou \(\ge\) e onde \(a \neq 0\). |
| + | |||
| + | Para a resolução de uma inequação quadrática precisamos de calcular as soluções da equação \(ax^2+bx+c=0\). Esse cálculo é feito através da [[Fórmulas resolventes|fórmula resolvente]] para equações do 2ºgrau. | ||
| + | |||
| + | \(\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\). | ||
| + | |||
| + | Seja \(\Delta=b^2-4ac\) o discriminante. Temos três casos: | ||
| + | * Se \(\Delta=0\) a equação tem apenas uma solução \(x=-b/2a\); | ||
| + | * Se \(\Delta >0\) a equação apresenta duas soluções reais distintas (consideremos essas soluções \(x_1\) e \(x_2\), \(x_1<x_2\)); | ||
| + | * Por fim, se \(\Delta<0\) a equação não tem soluções reais. | ||
| + | |||
| + | Consideremos a inequação quadrática do tipo \(ax^2+bx+c \le 0\) (os outros casos podem ser estudados da mesma forma). | ||
| + | |||
| + | Quando \(\Delta<0\), ou seja, quando a equação \(ax^2+bx+c=0\) não tem soluções reais, então temos dois casos: | ||
| + | |||
| + | * Se \(a>0\) a inequação não tem soluções reais; | ||
| + | * Se \(a<0\) a inequação é válida para \(x \in \mathbb{R}\). | ||
| + | |||
| + | No caso em que \(\Delta =0\) temos que: | ||
| + | |||
| + | * Se \(a>0\) a inequação tem apenas uma solução real; | ||
| + | * Se \(a<0\) a inequação é válida para \(x \in \mathbb{R}\). | ||
| + | |||
| + | Finalmente se \(\Delta>0\) temos que: | ||
| + | |||
| + | * Se \(a>0\) a inequação é válida no intervalo \([x_1,x_2]\); | ||
| + | * Se \(a<0\) a inequação é válida em \(]-\infty, x_1] \cup [x_2, +\infty[\). | ||
| + | | | ||
| + | | | ||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta <0\) e \(a>0\)''' | ||
| + | |- | ||
| + | ! style="background: #87CEEB;" | \(x\) | ||
| + | ! style="background: #87CEEB;" | \(-\infty\) | ||
| + | ! style="background: #87CEEB;" | \(\quad\) | ||
| + | ! style="background: #87CEEB;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta <0\) e \(a<0\)''' | ||
| + | |- | ||
| + | ! style="background: #87CEEB;" | \(x\) | ||
| + | ! style="background: #87CEEB;" | \(-\infty\) | ||
| + | ! style="background: #87CEEB;" | \(\quad\) | ||
| + | ! style="background: #87CEEB;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta =0\) e \(a>0\)''' | ||
| + | |- | ||
| + | ! style="background: #90EE90;" | \(x\) | ||
| + | ! style="background: #90EE90;" | \(-\infty\) | ||
| + | ! style="background: #90EE90;" | \(-b/2a\) | ||
| + | ! style="background: #90EE90;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta =0\) e \(a<0\)''' | ||
| + | |- | ||
| + | ! style="background: #90EE90;" | \(x\) | ||
| + | ! style="background: #90EE90;" | \(-\infty\) | ||
| + | ! style="background: #90EE90;" | \(-b/2a\) | ||
| + | ! style="background: #90EE90;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta>0\) e \(a>0\)''' | ||
| + | |- | ||
| + | ! style="background: #EE8262;" | \(x\) | ||
| + | ! style="background: #EE8262;" | \(-\infty\) | ||
| + | ! style="background: #EE8262;" | \(x_1\) | ||
| + | ! style="background: #EE8262;" | \(\quad\) | ||
| + | ! style="background: #EE8262;" | \(x_2\) | ||
| + | ! style="background: #EE8262;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |+'''\(\Delta>0\) e \(a<0\)''' | ||
| + | |- | ||
| + | ! style="background: #EE8262;" | \(x\) | ||
| + | ! style="background: #EE8262;" | \(-\infty\) | ||
| + | ! style="background: #EE8262;" | \(x_1\) | ||
| + | ! style="background: #EE8262;" | \(\quad\) | ||
| + | ! style="background: #EE8262;" | \(x_2\) | ||
| + | ! style="background: #EE8262;" | \(+\infty\) | ||
| + | |- | ||
| + | | \(ax^2+bx+c\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
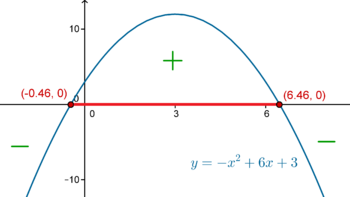
| + | [[Ficheiro:Ineq2grau2.png|thumb|right|350px|'''Figura 2 -'''A função quadrática \(-x^2+6x+3\) é maior ou igual a zero para valores de \(x\) compreendidos entre \(3-2\sqrt{3}\) e \(3+2\sqrt{3}\) inclusivé.]] | ||
| + | <span style="color:#4682B4">'''''Exemplos'''''</span> | ||
| + | |||
| + | Como resolver a inequação \((x+3)^2 \ge 2x^2+6\)? | ||
| + | |||
| + | Começamos por simplificar a inequação: \(x^2+6x+9 \ge 2x^2+6 \, \Longleftrightarrow \, -x^2+6x+3 \ge 0\). | ||
| + | |||
| + | O passo seguinte é determinar as soluções da equação \(-x^2+6x+3=0\). Através da fórmula resolvente obtemos, | ||
| + | |||
| + | \(\displaystyle x=\frac{-6 \pm \sqrt{6^2-4 \times (-1) \times 3}}{-2} \, \Longleftrightarrow \, x=3-2\sqrt{3} \, \vee \, x=3+2\sqrt{3}\) | ||
| + | |||
| + | Organizando a informação num quadro de sinal, | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |- | ||
| + | ! style="background: #FFFACD;"| \(x\) | ||
| + | ! style="background: #FFFACD;"| \(-\infty\) | ||
| + | ! style="background: #FFFACD;"| \(3-2\sqrt{3}\) | ||
| + | ! style="background: #FFFACD;"| \(\quad\) | ||
| + | ! style="background: #FFFACD;"| \(3+2\sqrt{3}\) | ||
| + | ! style="background: #FFFACD;"| \(+\infty\) | ||
| + | |- | ||
| + | | \(-x^2+6x+3\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |||
| + | A inequação \(-x^2+6x+3 \ge 0\) é assim válida no intervalo \([3-2\sqrt{3},3+2\sqrt{3}]\), ver figura 2. | ||
| + | |||
| + | |||
| + | ==Inequações com funções racionais== | ||
| + | |||
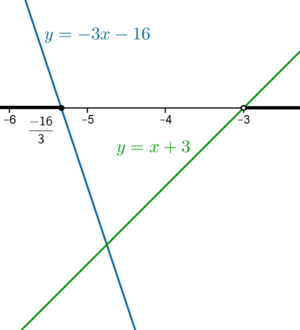
| + | [[Ficheiro:Ineqracional2.png|thumb|right|300px|'''Figura 3 -'''As duas retas tomam valores com sinais contrários (valores cuja divisão é negativa) para valores de \(x\) inferiores a \(\displaystyle \frac{-16}{3}\) e superiores a \(-3\).]] | ||
| + | Por simplicidade vamos apenas considerar inequações do tipo | ||
| + | |||
| + | \(\displaystyle\frac{p(x)}{q(x)}\leq 0\) | ||
| + | |||
| + | onde \(p\) e \(q\) são polinómios de grau 1 ou 2 (a desigualdade pode ser \(\geq\), \(>\) ou \(<\)). | ||
| + | |||
| + | Na resolução deste tipo de inequações com funções racionais existe mais um fator a ter em conta que é o facto do denominador nunca se poder anular. | ||
| + | Vejamos o seguinte exemplo: | ||
| + | |||
| + | \(\displaystyle \frac{2x-1}{x+3} \le 5\) | ||
| + | |||
| + | Neste exemplo, temos de garantir que o valor que anula o denominador não aparece como solução da inequação, ou seja, que \(x+3 \neq 0 \, \Leftrightarrow \, x \neq -3\). | ||
| + | |||
| + | Resolvendo a inequação temos então que, | ||
| + | |||
| + | \(\displaystyle \frac{2x-1}{x+3} -5 \le 0 \, \Longleftrightarrow \, \frac{2x-1-5x-15}{x+3} \le 0 \, \Longleftrightarrow \, \frac{-3x-16}{x+3} \le 0\). | ||
| + | |||
| + | Considerando o quadro de sinal seguinte, temos que: | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |- | ||
| + | ! style="background: #FFFACD;"| \(x\) | ||
| + | ! style="background: #FFFACD;"| \(-\infty\) | ||
| + | ! style="background: #FFFACD;"| \(-16/3\) | ||
| + | ! style="background: #FFFACD;"| \(\quad\) | ||
| + | ! style="background: #FFFACD;"| \(-3\) | ||
| + | ! style="background: #FFFACD;"| \(+\infty\) | ||
| + | |- | ||
| + | | \(-3x-16\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | |- | ||
| + | | \(x+3\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |- | ||
| + | | \((-3x-16)/(x+3)\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(\mbox{não definido}\) | ||
| + | | \(-\) | ||
| + | |} | ||
| + | |||
| + | Logo, a inequação \(\displaystyle \frac{-3x-16}{x+3} \le 0\) é válida no intervalo \(]-\infty, -16/3] \cup ]-3, +\infty[\), ver figura 3. | ||
| + | |||
| + | |||
| + | <span style="color:#4682B4">'''''Exemplos'''''</span> | ||
| + | |||
| + | Como resolver a inequação \(\displaystyle \frac{(x-5)(x+1)}{x^2-2x+1} <0\)? | ||
| + | |||
| + | Para resolver esta inequação basta conhecermos os valores que anulam cada um dos fatores do numerador, que são \(x=5\) e \(x=-1\) respectivamente, e os valores que anulam o denominador. Através da fórmula resolvente para equações do 2º grau descobrimos que o denominador desta inequação se anula em \(x=1\). Este valor, \(x=1\), não poderá fazer parte do conjunto ou intervalo de valores que são solução desta inequação pois é o valor que anula o denominador. | ||
| + | |||
| + | Organizando esta informação num quadro de sinais temos então que: | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" style="text-align: center;" | ||
| + | |- | ||
| + | | \(x\) | ||
| + | | \(-\infty\) | ||
| + | | \(-1\) | ||
| + | | \(\quad\) | ||
| + | | \(1\) | ||
| + | | \(\quad\) | ||
| + | | \(5\) | ||
| + | | \(+\infty\) | ||
| + | |- | ||
| + | | \(x-5\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |- | ||
| + | | \(x+1\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | |- | ||
| + | | \(x^2-2x+1\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | | \(+\) | ||
| + | |- | ||
| + | | \((x-5)(x+1)/(x^2-2x+1)\) | ||
| + | | \(+\) | ||
| + | | \(0\) | ||
| + | | \(-\) | ||
| + | | \(\mbox{nd}\) | ||
| + | | \(-\) | ||
| + | | \(0\) | ||
| + | | \(+\) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Concluímos então que o conjunto-solução da inequação é \(]-1,1[ \cup ]1,5[\). | ||
==Inequações com módulo== | ==Inequações com módulo== | ||
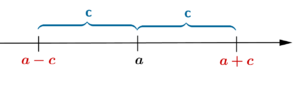
| + | [[Ficheiro:Ineqmodulo1.png|thumb|right|300px|'''Figura 4 -''' Caso em que \(c>0\).]] | ||
| + | Consideremos a inequação \(|x-a| \le c\). Qual será o significado desta inequação? | ||
| + | Ora, \(|x-a|\) representa a distância entre os pontos \(x\) e \(a\), em \(\mathbb{R}\). Portanto, a inequação \(|x-a| \le c\) representa os pontos \(x\) que estão a uma distância de \(a\) inferior ou igual a \(c\). | ||
| − | ---- | + | * Se \(c<0\) a inequação é impossível, uma vez que não existem distâncias negativas, isto é \(|x-a| \ge 0\); |
| + | * Se \(c=0\), a inequação \(|x-a| \le 0\) tem uma única soluçao quando \(x=a\); | ||
| + | * Já se \(c>0\), \(|x-a| \le c \, \Leftrightarrow \, -c \le x-a \le c \, \Leftrightarrow \, a-c \le x \le a+c\). | ||
| + | |||
| + | |||
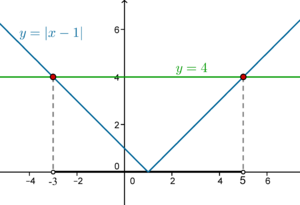
| + | [[Ficheiro:Ineqmodulo22.png|thumb|right|300px|'''Figura 5 -''' Os objetos da função módulo representada têm imagem inferior a \(4\) para valores de \(x\) entre \(-3\) e \(5\), exclusivé. ]] | ||
| + | Consideremos então a inequação \(|x-1|<4\). Esta condição representa os pontos \(x \in \mathbb{R}\) cuja distância ao ponto \(1\) é inferior a \(4\). Resolvemos este tipo de inequações da seguinte forma: | ||
| + | |||
| + | \(|x-1| <4 \, \Longleftrightarrow \, x-1<4 \, \wedge \, x-1>-4 \, \Longleftrightarrow \, x<5 \, \wedge \, x>-3\). | ||
| + | |||
| + | Logo a inequação é válida no intervalo \(]-3,5[\), ver figura 5. | ||
| + | |||
| + | |||
| + | Consideremos agora a inequação \(|x+5| \ge 2\). A condição representa o conjunto dos pontos \(x\) (em \(\mathbb{R}\)) cuja distância ao ponto \(-5\) é superior ou igual a 2. Resolvemos este tipo de inequações da seguinte forma: | ||
| + | |||
| + | \(|x+5| \ge 2 \, \Longleftrightarrow \, x+5 \ge 2 \, \vee \, x+5 \le -2 \, \Longleftrightarrow \, x \ge -3 \, \vee \, x \le -7\). | ||
| + | |||
| + | Neste caso, o intervalo que é solução desta inequação é \(]-\infty, -7] \cup [-3, +\infty[\). | ||
| + | |||
| + | |||
| + | Considerando a inequação \(|x-2|^2-|x| \le 0\) temos dois casos a considerar. Se \(x \ge 0\), a inequação fica na forma \(|x-2|^2-x \le 0\), enquanto que se \(x<0\) a inequação fica na forma \(|x-2|^2+x \le 0\). Ora então, | ||
| + | |||
| + | Temos que se \(x \ge 0\), | ||
| + | |||
| + | \(|x-2|^2-x \le 0 \, \Longleftrightarrow \, x^2-4x+4-x \le 0 \, \Longleftrightarrow \, x^2-5x+4 \le 0 \, \Longleftrightarrow \, (x-1)(x-4) \le 0 \, \Longleftrightarrow \, 1 \le x \le 4\) | ||
| + | |||
| + | Para o caso em que \(x<0\), | ||
| + | |||
| + | \(|x-2|^2+x \le 0 \, \Longleftrightarrow \, x^2-4x+4+x \le 0 \, \Longleftrightarrow \, x^2-3x+4\le 0 \, \Longleftrightarrow \, x \in \mathbb{R}\). | ||
| + | |||
| + | Portanto, o intervalo que é solução desta inequação é \([1,4]\). | ||
| + | |||
| + | |||
| + | ---- <br>Criada em 12 de Junho de 2013<br> Revista em 3 de Julho de 2013<br> Aceite pelo editor em 30 de Junho de 2017<br> | ||
| + | [[Category:Matemática]] | ||
Edição actual desde as 10h37min de 12 de julho de 2021
Referência : Tavares, J., Geraldo, A., (2017) Inequações, Rev. Ciência Elem., V5(2):073
Autor: João Nuno Tavares e Ângela Geraldo
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2017.073]

Índice |
Definição
Uma inequação em \(\mathbb{R}\) a uma incógnita é uma desigualdade que contem uma variável real. Assim, dá-se o nome de inequação a uma desigualdade à qual não se pode atribuir um valor de verdade (dizer se é verdadeira ou falsa), porque o seu valor de verdade depende do valor numérico que for atribuído à variável.
São exemplos de inequações: \(2x+3 > 10\), \(\quad 8-z \ge 11\) e \(-2a^2+3 \le 7a\), onde \(x,z,a\in \mathbb{R}\).
Resolver uma inequação é determinar os conjuntos ou os intervalos de valores que se podem atribuir à variável de modo a tornar a desigualdade verdadeira.
Inequações de 1º grau
A resolução de inequações do 1ºgrau comporta os mesmos desafios e os mesmos procedimentos que a resolução de equações do 1ºgrau. Assim, o objetivo principal da resolução de inequações do 1ºgrau será isolar a incógnita num dos membros, ou seja, obter \(x> \dots\), \(\quad x < \dots\), \(\quad x \le \dots\) ou \(\quad x \ge \dots\). Na resolução destas inequações podemos utilizar as propriedades das desigualdades de forma a não modificar o seu valor de verdade. Para isso, podemos transformar a desigualdade por adição, subtração, multiplicação e divisão por um número positivo como fazemos na resolução de equações. No caso da multiplicação ou divisão por um número negativo, existe uma diferença essencial relativamente às equações, pois no caso das inequações será necessário alterar o sentido da desigualdade para manter o mesmo valor de verdade.
Qualquer inequação do 1ºgrau, pode ser reduzida, através das operações referidas anteriormente, a uma das quatro formas seguintes:
\(ax < b\), \(\quad ax > b\), \(\quad ax \le b \quad\) ou \(\quad ax \ge b\)
podendo \(a\) ser positivo ou negativo mas nunca nulo.
Exemplos
Como resolver a equação \(\displaystyle 2- \frac{x-3}{2} \le 5\)?
\(\displaystyle 2- \frac{x-3}{2} \le 5 \, \Longleftrightarrow \, 4-x+3 \le 10 \, \Longleftrightarrow \, -x \le 3 \, \Longleftrightarrow \, x \ge -3\)
Logo o conjunto-solução desta inequação é \(\quad [-3, +\infty[ \), ver esquema figura 1.
Inequações de 2º grau
| Uma inequação do 2ºgrau (ou inequação quadrática) é uma inequação em que a incógnita toma grau dois num dos termos. Ou seja, é uma inequação do tipo
\(ax^2+bx+c \le 0\) em que o sinal da desigualdade pode ser \(>, <, \le\) ou \(\ge\) e onde \(a \neq 0\). Para a resolução de uma inequação quadrática precisamos de calcular as soluções da equação \(ax^2+bx+c=0\). Esse cálculo é feito através da fórmula resolvente para equações do 2ºgrau. \(\displaystyle x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\). Seja \(\Delta=b^2-4ac\) o discriminante. Temos três casos:
Consideremos a inequação quadrática do tipo \(ax^2+bx+c \le 0\) (os outros casos podem ser estudados da mesma forma). Quando \(\Delta<0\), ou seja, quando a equação \(ax^2+bx+c=0\) não tem soluções reais, então temos dois casos:
No caso em que \(\Delta =0\) temos que:
Finalmente se \(\Delta>0\) temos que:
|
|
Exemplos
Como resolver a inequação \((x+3)^2 \ge 2x^2+6\)?
Começamos por simplificar a inequação: \(x^2+6x+9 \ge 2x^2+6 \, \Longleftrightarrow \, -x^2+6x+3 \ge 0\).
O passo seguinte é determinar as soluções da equação \(-x^2+6x+3=0\). Através da fórmula resolvente obtemos,
\(\displaystyle x=\frac{-6 \pm \sqrt{6^2-4 \times (-1) \times 3}}{-2} \, \Longleftrightarrow \, x=3-2\sqrt{3} \, \vee \, x=3+2\sqrt{3}\)
Organizando a informação num quadro de sinal,
| \(x\) | \(-\infty\) | \(3-2\sqrt{3}\) | \(\quad\) | \(3+2\sqrt{3}\) | \(+\infty\) |
|---|---|---|---|---|---|
| \(-x^2+6x+3\) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
A inequação \(-x^2+6x+3 \ge 0\) é assim válida no intervalo \([3-2\sqrt{3},3+2\sqrt{3}]\), ver figura 2.
Inequações com funções racionais
Por simplicidade vamos apenas considerar inequações do tipo
\(\displaystyle\frac{p(x)}{q(x)}\leq 0\)
onde \(p\) e \(q\) são polinómios de grau 1 ou 2 (a desigualdade pode ser \(\geq\), \(>\) ou \(<\)).
Na resolução deste tipo de inequações com funções racionais existe mais um fator a ter em conta que é o facto do denominador nunca se poder anular. Vejamos o seguinte exemplo:
\(\displaystyle \frac{2x-1}{x+3} \le 5\)
Neste exemplo, temos de garantir que o valor que anula o denominador não aparece como solução da inequação, ou seja, que \(x+3 \neq 0 \, \Leftrightarrow \, x \neq -3\).
Resolvendo a inequação temos então que,
\(\displaystyle \frac{2x-1}{x+3} -5 \le 0 \, \Longleftrightarrow \, \frac{2x-1-5x-15}{x+3} \le 0 \, \Longleftrightarrow \, \frac{-3x-16}{x+3} \le 0\).
Considerando o quadro de sinal seguinte, temos que:
| \(x\) | \(-\infty\) | \(-16/3\) | \(\quad\) | \(-3\) | \(+\infty\) |
|---|---|---|---|---|---|
| \(-3x-16\) | \(+\) | \(0\) | \(-\) | \(-\) | \(-\) |
| \(x+3\) | \(-\) | \(-\) | \(-\) | \(0\) | \(+\) |
| \((-3x-16)/(x+3)\) | \(-\) | \(0\) | \(+\) | \(\mbox{não definido}\) | \(-\) |
Logo, a inequação \(\displaystyle \frac{-3x-16}{x+3} \le 0\) é válida no intervalo \(]-\infty, -16/3] \cup ]-3, +\infty[\), ver figura 3.
Exemplos
Como resolver a inequação \(\displaystyle \frac{(x-5)(x+1)}{x^2-2x+1} <0\)?
Para resolver esta inequação basta conhecermos os valores que anulam cada um dos fatores do numerador, que são \(x=5\) e \(x=-1\) respectivamente, e os valores que anulam o denominador. Através da fórmula resolvente para equações do 2º grau descobrimos que o denominador desta inequação se anula em \(x=1\). Este valor, \(x=1\), não poderá fazer parte do conjunto ou intervalo de valores que são solução desta inequação pois é o valor que anula o denominador.
Organizando esta informação num quadro de sinais temos então que:
| \(x\) | \(-\infty\) | \(-1\) | \(\quad\) | \(1\) | \(\quad\) | \(5\) | \(+\infty\) |
| \(x-5\) | \(-\) | \(-\) | \(-\) | \(-\) | \(-\) | \(0\) | \(+\) |
| \(x+1\) | \(-\) | \(0\) | \(+\) | \(+\) | \(+\) | \(+\) | \(+\) |
| \(x^2-2x+1\) | \(+\) | \(+\) | \(+\) | \(0\) | \(+\) | \(+\) | \(+\) |
| \((x-5)(x+1)/(x^2-2x+1)\) | \(+\) | \(0\) | \(-\) | \(\mbox{nd}\) | \(-\) | \(0\) | \(+\) |
Concluímos então que o conjunto-solução da inequação é \(]-1,1[ \cup ]1,5[\).
Inequações com módulo
Consideremos a inequação \(|x-a| \le c\). Qual será o significado desta inequação?
Ora, \(|x-a|\) representa a distância entre os pontos \(x\) e \(a\), em \(\mathbb{R}\). Portanto, a inequação \(|x-a| \le c\) representa os pontos \(x\) que estão a uma distância de \(a\) inferior ou igual a \(c\).
- Se \(c<0\) a inequação é impossível, uma vez que não existem distâncias negativas, isto é \(|x-a| \ge 0\);
- Se \(c=0\), a inequação \(|x-a| \le 0\) tem uma única soluçao quando \(x=a\);
- Já se \(c>0\), \(|x-a| \le c \, \Leftrightarrow \, -c \le x-a \le c \, \Leftrightarrow \, a-c \le x \le a+c\).
Consideremos então a inequação \(|x-1|<4\). Esta condição representa os pontos \(x \in \mathbb{R}\) cuja distância ao ponto \(1\) é inferior a \(4\). Resolvemos este tipo de inequações da seguinte forma:
\(|x-1| <4 \, \Longleftrightarrow \, x-1<4 \, \wedge \, x-1>-4 \, \Longleftrightarrow \, x<5 \, \wedge \, x>-3\).
Logo a inequação é válida no intervalo \(]-3,5[\), ver figura 5.
Consideremos agora a inequação \(|x+5| \ge 2\). A condição representa o conjunto dos pontos \(x\) (em \(\mathbb{R}\)) cuja distância ao ponto \(-5\) é superior ou igual a 2. Resolvemos este tipo de inequações da seguinte forma:
\(|x+5| \ge 2 \, \Longleftrightarrow \, x+5 \ge 2 \, \vee \, x+5 \le -2 \, \Longleftrightarrow \, x \ge -3 \, \vee \, x \le -7\).
Neste caso, o intervalo que é solução desta inequação é \(]-\infty, -7] \cup [-3, +\infty[\).
Considerando a inequação \(|x-2|^2-|x| \le 0\) temos dois casos a considerar. Se \(x \ge 0\), a inequação fica na forma \(|x-2|^2-x \le 0\), enquanto que se \(x<0\) a inequação fica na forma \(|x-2|^2+x \le 0\). Ora então,
Temos que se \(x \ge 0\),
\(|x-2|^2-x \le 0 \, \Longleftrightarrow \, x^2-4x+4-x \le 0 \, \Longleftrightarrow \, x^2-5x+4 \le 0 \, \Longleftrightarrow \, (x-1)(x-4) \le 0 \, \Longleftrightarrow \, 1 \le x \le 4\)
Para o caso em que \(x<0\),
\(|x-2|^2+x \le 0 \, \Longleftrightarrow \, x^2-4x+4+x \le 0 \, \Longleftrightarrow \, x^2-3x+4\le 0 \, \Longleftrightarrow \, x \in \mathbb{R}\).
Portanto, o intervalo que é solução desta inequação é \([1,4]\).
Criada em 12 de Junho de 2013
Revista em 3 de Julho de 2013
Aceite pelo editor em 30 de Junho de 2017