Forças Conservativas e Energia Potencial
Referência : Ferreira, M., (2013) Forças conservativas e energia potencial, Rev. Ciência Elem., V1(1):012
Autor: Miguel Ferreira
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2013.012]

Uma força diz-se conservativa quando o trabalho realizado é independente da trajectória descrita, dependendo apenas das posições inicial e final. Em particular, quando a trajectória é fechada, ou seja, quando as posições inicial e final coincidem, o trabalho realizado pela força conservativa é nulo.
O carácter conservativo de uma força implica que o trabalho seja uma grandeza posicional, podendo ser expresso à partir da variação de uma energia potencial, 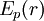 ,associada ao campo de forças que dá origem à interacção. A energia potencial é uma função da posição que depende da configuração do sistema. O leitor, com certeza, conhece a energia potencial gravitacional. Outras formas de energia potencial são a elástica e a electrostática.
,associada ao campo de forças que dá origem à interacção. A energia potencial é uma função da posição que depende da configuração do sistema. O leitor, com certeza, conhece a energia potencial gravitacional. Outras formas de energia potencial são a elástica e a electrostática.
- Teorema da conservação da energia mecânica
Consideremos uma força conservativa.O trabalho realizado pela uma força ao deslocar o seu ponto de aplicação do ponto A até ao ponto B pode ser escrito à custa da variação de energia potencial associada ao campo de força:
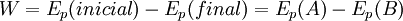
Tomando:
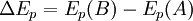 , (1)
, (1)
ficamos com 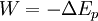 .
.
Consideremos agora o teorema do trabalho-energia:
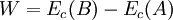 , (2)
, (2)
em que 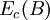 e
e 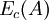 são as energia cinéticas da partícula quando passa pelas posições B e A, respectivamente. Tendo em consideração as equações (1) e (2), podemos escrever:
são as energia cinéticas da partícula quando passa pelas posições B e A, respectivamente. Tendo em consideração as equações (1) e (2), podemos escrever:
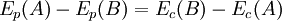 ,
,
ou seja:
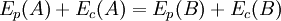 ,
,
independentemente dos pontos A e B considerados. À soma das energias cinética e potencial designa-se por energia mecânica. Da última expressão concluímos que a energia mecânica do corpo sujeito apenas à acção da força conservativa é constante. Este é o enunciado do teorema da conservação da energia mecânica.
Criada em 17 de Outubro de 2010
Revista em 11 de Junho de 2011
Aceite pelo editor em 12 de Junho de 2011

