e na computação
Referência : Vasconcelos, P. B., (2022) O que é o e para o computador?, Rev. Ciência Elem., V10(1):005
Autor: Paulo Beleza de Vasconcelos
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2022.005]

[editar] Resumo
Como é que o computador ou a máquina de calcular nos fornecem o valor de \(e\)? E de \(e^{0,1}\)? A mesma questão pode ser colocada para o valor de outras funções num ponto: por exemplo, \(\sin\), \(\cos\) e \(\log\). Se se pensar que um computador trabalha apenas com as operações elementares “\(+\)”, “\(—\)”, “\(\times\)” e “\(/\)”, então o cálculo deve passar por exprimir a função exponencial em termos destas operações.
Motivação
Como aproximar \(e^{0,1}\)?
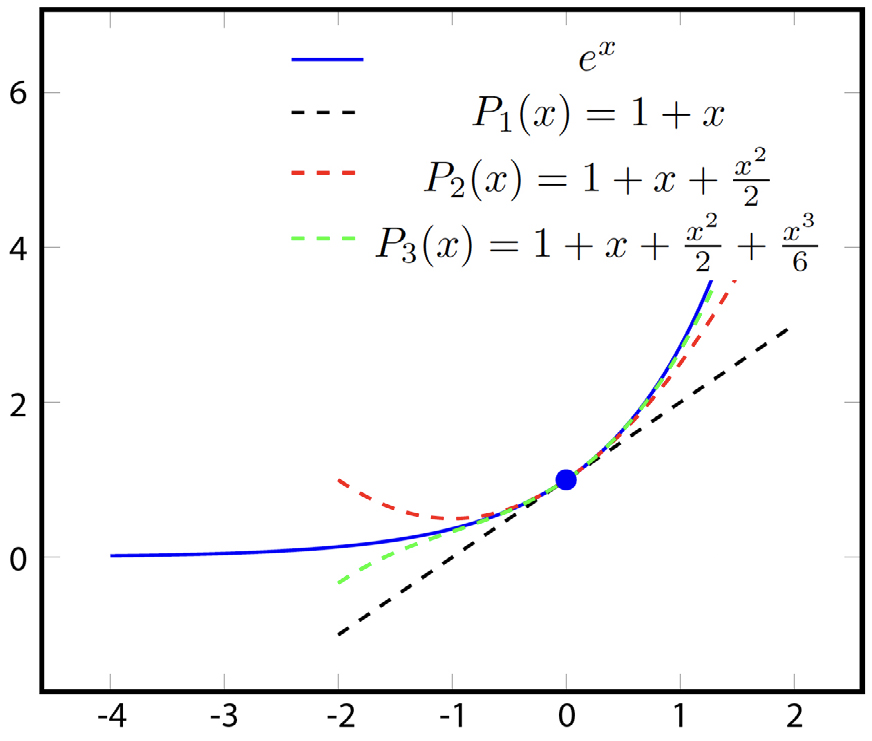
Considere-se \(f (x) = e^x\) uma função infinitamente derivável em \(0\). Ora, sabe-se que \(f (0) = e^0 = 1\). Como a derivada da função exponencial é a própria função exponencial, então \(f′ (0) = e^0 = 1\). Sabendo a imagem de \(f\) e da sua derivada na origem, pode- se construir a reta tangente a \(f\) em \(0: y = f (0) + f′ (0) x = 1 + x\). Para pontos \(x\) próximos da origem, a reta tangente permite-nos obter uma boa aproximação para \(f (x)\). Ou seja, \(e^{0,1}\approx e^{0}+e^{0}\times 0,1=1,1\). Ora o valor fornecido pelo computador é: \(1,105170918075648\), pelo que se tem uma casa decimal correta.
Como melhorar? Bem, se no caso anterior se construir a reta tangente, polinómio de grau 1, \(P_1 (x)\), tal que \(f (0) = P_1 (0)\) e \(f′ (0) = P′1 (0)\), então pode-se tentar construir um polinómio de grau 2 na condição de adicionalmente satisfazer \(f"\left ( 0 \right )=P_{2}^{"}\left ( 0 \right )\). Assim, sendo \(P_2 (x) = a + bx + cx^2\), tem-se que \(P_2\left ( 0 \right )=a,P_{2}^{'}\left ( 0 \right )=b\) e \(P_{2}^{"}\left ( 0 \right )=2c\). Pelo que \(a = e^0 = 1\), \(b = e^0 = 1\) e \(2c = e^0 = 1\), donde o polinómio de segundo grau que verifica as três condições anteriores é \(P_2\left ( x \right )=1+x+\frac{1}{2}x^{2}\). Pode-se então aproximar “melhor” \(e^{0,1}\) através de \(P_2 (0,1) = 1+0,1 + 0, 005 = 1, 105\), e passa-se a ter três casas decimais coincidentes.
Este processo pode ser continuado para um polinómio de grau \(n\) centrado em \(0\), \(0\), \(0,P_n\left ( x \right )=1+x+\frac{1}{2}x^{2}+\frac{1}{3}x^{3}+\cdots+\frac{1}{n!}x^{n}\), que se designa por polinómio de Taylor de grau \(n\) centrado em 0 (FIGURA 1).
Série de Taylor
Seja \(f (x)\) uma função infinitamente derivável. O polinómio de Taylor de grau \(n\) centrado em \(x_0\in \mathbb{R}\) vem dado por
\(P_n\left ( x \right )=\sum_{k=0}^{n}\frac{f^{\left ( k \right )}\left ( x_0 \right )}{k!}\left ( x-x_o \right )^{k}\)
sendo \(f^{\left ( k \right )}\) a derivada de ordem \(k\) de \(f\). Na verdade, o valor de \(n\) pode crescer até ao infinito (e mais além...). Define-se série de Taylor da função \(f\) centrada em \(x_0\) e avaliada em \(x\) à soma infinita
\(f\left ( x \right )=\sum_{k=0}^{\infty }\frac{f^{\left ( k \right )}\left ( x_0 \right )}{k!}\left ( x-x_0 \right )^{k}\).
Para a função exponencial, tem-se
\(e^{x}=\sum_{k=0}^{\infty }\frac{e^{x_{0}}}{k!}\left ( x-x_0 \right )^{k}\).
Quando a série se desenvolve em torno de \(x_0 = 0\) é designada por série de Maclaurin. A aproximação pelo polinómio de Taylor resulta então de truncar a série de Taylor num número finito de termos.
Várias questões se podem levantar:
- Para aproximar o valor de uma função num ponto, qual o valor de \(x_0\) a escolher? A função pode estar definida para todo o real, mas apenas na vizinhança de \(x_0\) a aproximação polinomial deve dar bons resultados. Como melhorar a aproximação?
- Que condições devem ser verificadas para que a série seja convergente? Na verdade poderá não haver convergência para um dado valor de \(x_0\), e polinómios com elevado grau trazem problemas ao cálculo numérico: crescimento rápido de \(n!\) (fração a convergir para zero muito rapidamente) e potências muito elevadas de \(\left ( x-x_0 \right )^{k}\).
Para melhorar o cálculo numérico pode-se evitar o cálculo explícito das potências e fatorial, basta verificar (método de Horner) que
\(e^{x}=1+x(1+\frac{x}{2}(1+\frac{x}{3}(1+\cdots\)
pode ser usado para exprimir a série de Taylor da função exponencial em torno de \(0\).
Análise do erro
Sendo \(P_n (x)\) o polinómio de Taylor de grau \(n\) centrado em \(x_0\), pode-se definir o erro absoluto em aproximar \(f (x)\) por \(P_n (x)\):
\(R_n\left ( x \right )=\left | f\left ( x \right )-P_n\left ( x \right ) \right |\).
No caso da função exponencial
\(R_n\left ( x \right )=\left | \frac{e^{\left ( n+1 \right )c}}{\left ( n+1 \right )!}\left ( x-x_0 \right )^{n+1} \right |\)
\(=\left | e^{c}\frac{e^{\left ( n+1 \right )}}{\left ( n+1 \right )!}\left ( x-x_0 \right )^{n+1} \right |\)
sendo \(c\) um valor real que satisfaz \(x_0 \leq c \leq x\). Ora como a função exponencial é crescente, então atinge o maior valor no extremo direito do intervalo \([x_0, x]\). Então, o erro absoluto é majorado por
\(R_n\left ( x \right )\leq \left | e^{x}\frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |\)
e o relativo por
\(\frac{R_n\left ( x \right )}{e^{x}}\leq \left | \frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |\).
Note-se que \(\left | P_{n+1}\left ( x \right )-P_n\left ( x \right ) \right |=\left | \frac{\left ( x-x_0 \right )^{n+1}}{\left ( n+1 \right )!} \right |\), e o erro relativo em \(P_n (x)\) é majorado pelo termo de ordem \(n + 1\) da série de Taylor. Assim, pode-se determinar quantos termos \(n\) terão de ser considerados para que uma precisão de \(\textrm{tol}\) seja verificada: \(\left | \frac{\left ( x-x_0 \right )^{n}}{n!} \right |\leq \textrm{tol}\).
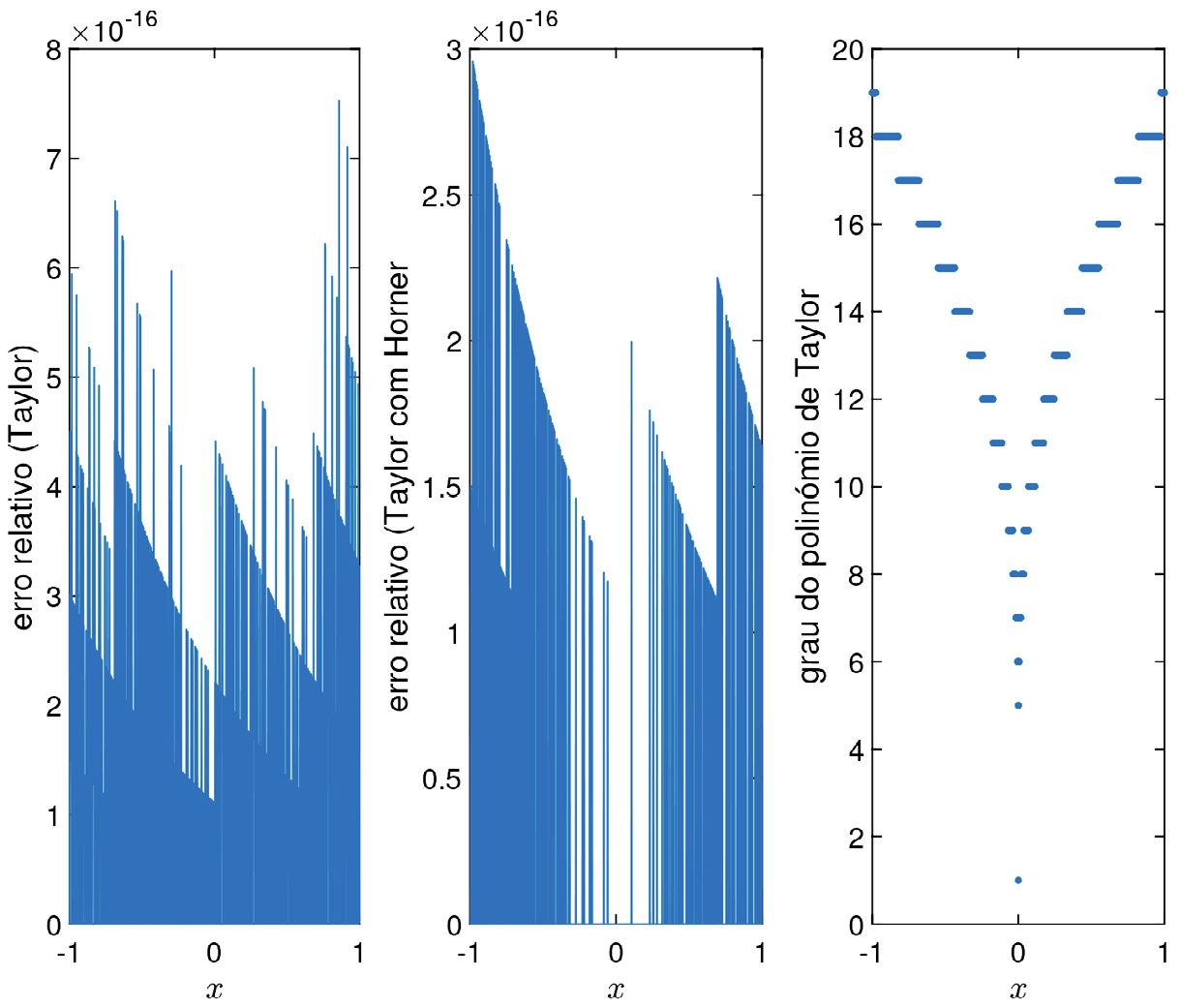
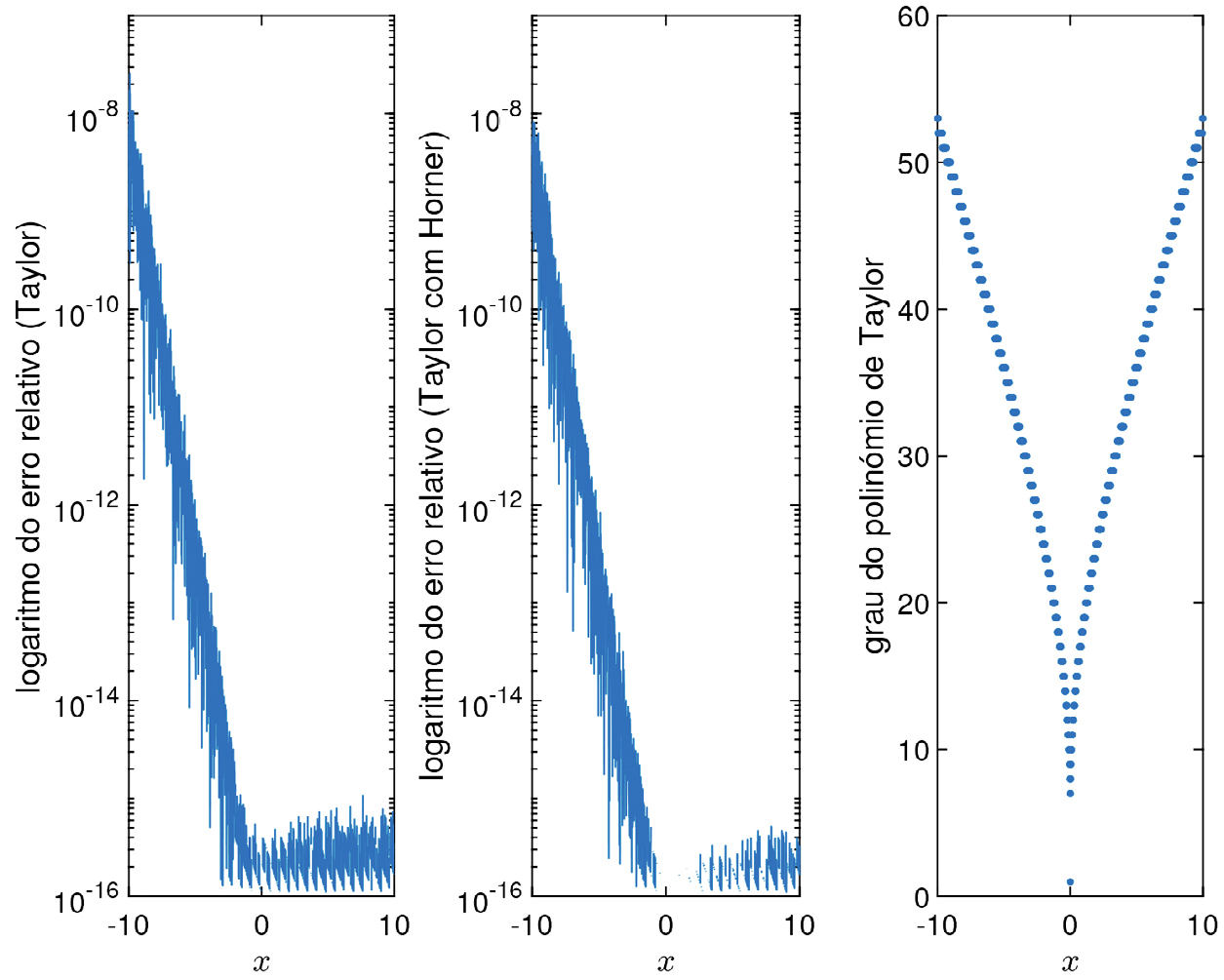
Na FIGURA 2 mostram-se os erros relativos ao aproximar \(e^{x}\), para \(x\in \left [ -1,1 \right ]\), usando polinómios de Taylor de grau \(n\), centrados em \(0\), a satisfazer \(\left | \frac{x^{n}}{n!} \right |\leq 10^{-16}\). À medida que o valor que se pretende aproximar se afasta de \(0\), o grau do polinómio a usar vai aumentando, mas a qualidade da aproximação vai sendo menos boa. Isso é cada vez mais evidente quanto maior for a amplitude de valores a considerar para \(x\) (FIGURA 3).
Redução da distância do argumento de aproximação
Pode-se recorrer a propriedades das funções para focar a aproximação e assim evitar usar grau polinomial elevado e com perda de qualidade de aproximação.
No caso da função exponencial sabe-se que \(P_n\left ( x \right )=\sum_{k=0}^{n}\frac{x^{k}}{k!}\) pode ser uma boa aproximação de \(ex\) desde que \(x\) seja próximo de \(0\). Então uma ideia seria a de “trazer” a aproximação de \(e^x\) para “perto” de \(e^0\). Ora se se considerar \(x=l\textrm{In}2+r\) para um inteiro positivo \(l\) e um real \(r\) com \(\left | r \right |\leq \frac{1}{2}\textrm{In}2\) (valor suficientemente próximo de zero) então, \(e^{x}=e^{l\textrm{In}2+r}=2^{l}e^{r}\).
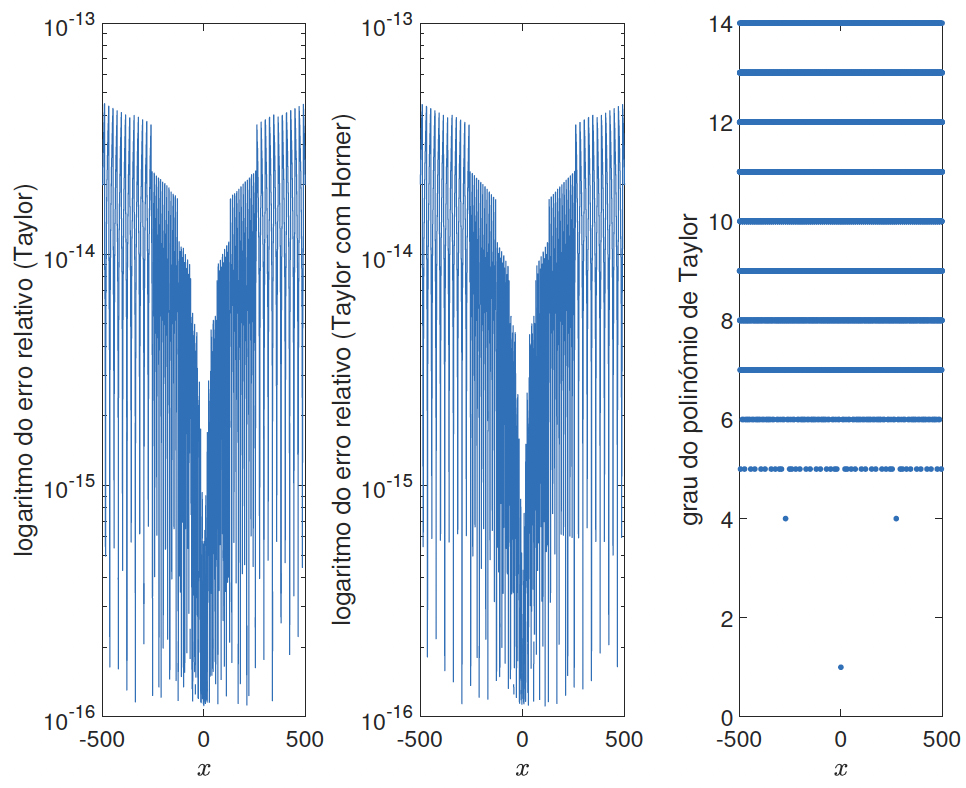
Resulta imediato que se pode aproximar \(e^x\) à custa da aproximação de Maclaurin da exponencial em \(r\) e de \(2(l)\) que é fácil e eficiente de calcular. Para que l seja inteiro e \(\left | r \right |\leq \frac{x^{n}}{n!}\), de \(l=\frac{x}{\textrm{In}2}-\frac{r}{\textrm{In}2}\) pode-se impor que \(l=\left \lceil \frac{x}{\textrm{In}2}-\frac{1}{2} \right \rceil\) (arredondamento para cima). Sabendo \(l\) e \(x\) calcula-se \(r\) e usa-se \(2^lP_n (r)\) para aproximar \(e^x = 2^le^r\). Da FIGURA 4 ilustra-se que, o erro relativo (em escala logarítmica) é muito bom mesmo para valores distantes de \(0\) sendo que, o grau polinomial usado foi no máximo de 14.
As aproximações são já muito boas: note-se que para aproximar \(e^{500}\approx 1, 03610^{217}\) se está a cometer um erro relativo de \(2\times 10^{-14}\) (i.e., erro na décima quarta casa decimal de um número imensamente grande).
Pode-se fazer ainda melhor recorrendo a abordagens mais sofisticadas e eficientes de efetuar a redução da distância do argumento de aproximação, mas sobretudo, considerando outras aproximações, como interpolação polinomial. Estas matérias de teoria de aproximação e de implementação em computador são abordadas em análise numérica e matemática computacional.
O número de Euler
Antes de terminar vai-se destacar que a aritmética efetuada num computador é em precisão finita. Num computador os números racionais têm de ser armazenados num espaço que é finito, em oposição à sua infinitude. Os computadores trabalham numa base 2, resultando daí que muitos números racionais não têm representação exata. Por exemplo, a fração decimal \(0,1\) não tem representação exata em base 2 mas tem em base 10 \(\left ( 0,1=1\times 10^{-1} \right )\).
A representação de números reais em computador segue, desde 1985, a norma IEEE-754 na utilização da aritmética binária para números de vírgula flutuante, relativo ao armazenamento, métodos de arredondamento, ocorrência de underflow/overflow e realização das operações aritméticas básicas. Um sistema de vírgula flutuante permite representar, com um número fixo de dígitos, números racionais com diferentes ordens de magnitude. A representação finita em base 2 usa 3 componentes: o sinal, o expoente e a mantissa: \(\left [ \pm \right ]\left [ \textrm{mantissa} \right ]\times 2^{\left [ \textrm{expoente} \right ]}\). O sistema a 64-bits (dupla precisão) usa 1 bit para o sinal, 11 para o expoente e 52 para a mantissa (sendo de 8 bits para o expoente e de 23 bits para a mantissa em precisão simples). O real \(0,1\) tem a seguinte representação binária em 64- bits: sinal \((0)\), expoente (\(01111111011\)) e mantissa 1001100110011001100110011001100110011001100110011010), a que corresponde, de volta à base 10, a melhor representação possível de
\(0.100000000000000005551115123126\).
É curioso testar no vosso computador que \(0,1 + 0, 2 − 0,3 = 5, 5511 \times 10^{-17}\) e não \(0\). Na verdade para o computador tal resultado deve ser considerado 0, pois o cálculo em precisão dupla fornece uma precisão relativa de cerca de 16 dígitos decimais.
A precisão de computador pode ser calculada através do épsilon de máquina: o menor número que separa 1 do próximo número representável (2, 2204 \times 10^{-16}). O épsilon de um número maior é também maior: o de \(100000\) é \(1, 4552 \times 10^{-11}\). Assim se efetuarem no vosso computador ou numa calculadora o seguinte cálculo \(10^{12}-10^{12}+10^{-5}\) o resultado será o esperado \(10^{-5}\), pois ao subtrair dois números com a mesma representação e adicionarem um terceiro, resulta o terceiro. Mas, a propriedade associativa não existe em vírgula flutuante: o cálculo de \(10^{12}-10^{-5}+10^{12}\) vale \(0\). Note-se que o épsilon de \(10^{12}\) é \(1,2207 \times 10^{-4}\) e portanto \(10^{12}+10^{-5}=10^{12}\). O próximo número representável após \(10^{12}\) é \(10^{12}+1,2207\times 10^{-4}\). Por este facto, os números reais em computador não são uniformemente espaçados. No standard IEEE 754, existe maior representatividade próximo de 0 do que para valores muito grandes em valor absoluto.
Sabe-se que e é irracional e que pode ser aproximado por \(\lim_{n\rightarrow \infty }\left ( 1+\frac{1}{n} \right )^{n}\) e que portanto este limite corresponde à soma da série de Taylor da função exponencial em torno de \(1:e=\sum_{k=0}^{\infty }\frac{1}{k!}\).
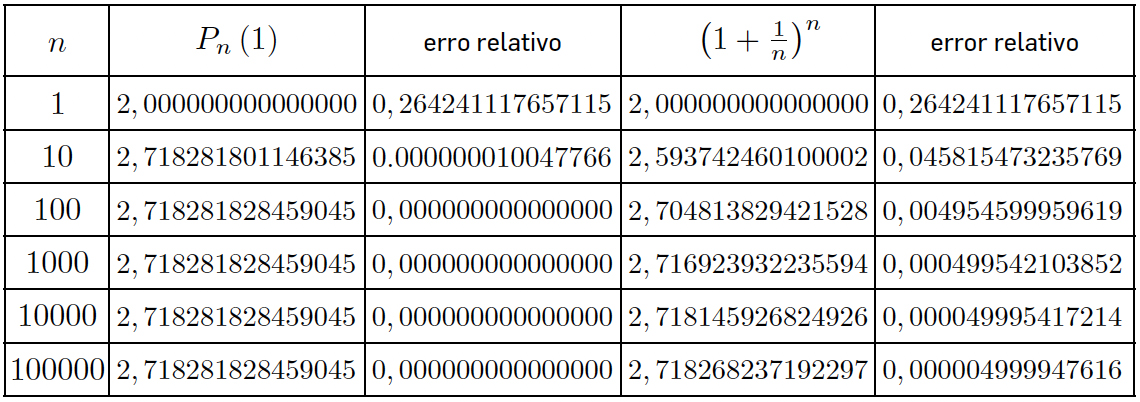
A TABELA 1 mostra as aproximações calculadas para e via polinómios de Taylor e através de \(\left ( 1+\frac{1}{n} \right )^{n}\), para valores crescentes de n. Ora com um polinómio de Taylor centrado na origem de grau 19 obtém-se quase a precisão máquina, sendo que para graus maiores não há melhoria na aproximação. Já para o cálculo via a expressão do limite, com \(n = 100000\) tem-se ainda um erro na sexta casa decimal. Poder-se-ia pensar que o erro relativo baixaria consistentemente para valores crescentes de \(n\). Tal não é o caso atendendo aos erros numéricos, que não vão permitir melhorar a aproximação de e com a expressão \(\left ( 1+\frac{1}{n} \right )^{n}\)
[editar] Referências
- BRISEBARRE, N. et al., A new range-reduction algorithm, IEEE Transactions on Computers, 54, 3, 331–339. 2005.
- FOUSSE, L. et al., A multiple-precision binary floating-point library with correct rounding, ACM Transactions on Mathematical Software (TOMS), 33, 2, 13. 2007.
- GORDON, S. P., Approximating functions with exponential functions, Problems, Resources, and Issues in Mathematics Undergraduate Studies, 15, 4, 349–362. 2005.
- TREFETHEN, L. N., Approximation Theory and Approximation Practice, Extended Edition, SIAM. 2019.
- WANG, L. et al., Efficient argument range reduction for implementation of double-precision floating-point exponential function, World Congress on Intelligent Control and Automation, 2, 6800–6803. IEEE. 2006.
Criada em 8 de Dezembro de 2021
Revista em 9 de Dezembro de 2021
Aceite pelo editor em 15 de Março de 2022

