Vírus, Poliedros, Arquitetura e… Matemática
Referência : Nápoles, M. S. M., (2022) Vírus, Poliedros, Arquitetura e… Matemática, Rev. Ciência Elem., V10(3):037
Autor: Maria Suzana Metello de Nápoles
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2022.037]

[editar] Resumo
A recente pandemia de Covid-19 motiva-nos a falar de vírus, de arquitetura e de poliedros. Como veremos, o elo entre estes três tópicos é a Matemática… que está em toda a parte.
Numa iniciativa conjunta da Sociedade Europeia de Matemática (EMS) e da Sociedade Europeia de Biologia Teórica e Matemática (ESMBT), celebrou-se, em 2018, o Ano da Biologia Matemática, com iniciativas científicas em diversos países da Europa.
Respondendo ao desafio de celebração dessa efeméride, a mostra Biologia Matemática sem fronteiras, promovida pelo Centro de Matemática, Aplicações Fundamentais e Investigação Operacional (CMAFcIO), incluiu resultados originais de diversos investigadores. O financiamento foi assegurado pela Faculdade de Ciências da Universidade de Lisboa e pela Fundação para a Ciência e a Tecnologia. Esta mostra, inaugurada em 12 de dezembro de 2018 e patente ao público até 31 de março de 2019, surgiu como um breve olhar sobre algumas das aplicações da Matemática na Biologia, exemplos de como eliminando fronteiras se consegue ir mais longe no conhecimento científico. Não pretendendo ser exaustiva, tentou mostrar de que forma estas duas áreas se têm cruzado ao longo do tempo, abrindo o caminho para explorar conquistas mais recentes. Um dos painéis desta mostra foi dedicado aos vírus.
A partir dessa data, a pandemia foi-se agravando em todo o mundo e nunca se falou tanto de Matemática como nos últimos tempos, com gráficos e previsões a encher jornais e noticiários televisivos. Mas, mais do que estimar como será a disseminação da doença, o número de infetados e as percentagens de mortes e hospitalizações, os modelos matemáticos permitem simular cenários e testar a eficácia de normas das autoridades de saúde e governamentais para reduzir o contágio, tais como o encerramento de escolas, o cancelamento de eventos públicos e a restrição de viagens. Menos de um ano depois, em 31 de dezembro de 2019, foi dado o primeiro alerta do governo chinês sobre o surgimento de um novo coronavírus e os primeiros casos em Portugal surgiram em março de 2020.
Os vírus, que só a microscopia eletrónica permitiu visualizar, são sistemas orgânicos simples compostos por material genético (ADN ou ARN) rodeado por um invólucro proteico, o capsídeo, constituído por subunidades proteicas idênticas, chamadas capsómeros e podendo ainda, ter uma membrana exterior designada envelope. O capsídeo tem duas funções: proteger o material genético e reconhecer o seu alvo. A sua estrutura é responsável pela forma como o vírus se forma, evolui e infeta os seus hospedeiros.
A modelação geométrica dos capsídeos virais permite indicar as orientações relativas das suas proteínas, contribuindo para avanços recentes na compreensão dos vírus e na terapia antiviral. O grupo dos vírus mais comum é o chamado icosaédrico. Este nome deve-se ao facto de terem capsídeos com a simetria de um icosaedro.
O icosaedro é um poliedro regular composto por triângulos equiláteros, que apresenta 20 faces, 12 vértices e 30 arestas.
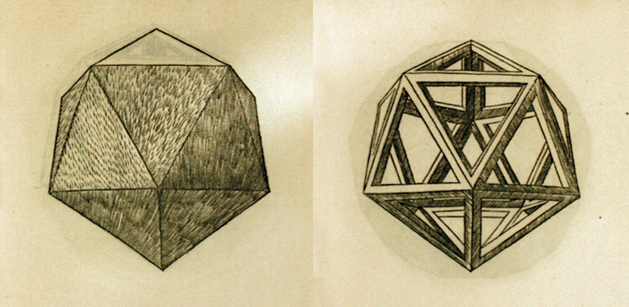
O estudo dos poliedros remonta ao século IV a.C. com a fundação da Academia de Platão que, rapidamente, se tornou o centro do estudo da Matemática e da Filosofia.
No diálogo Timeu, Platão inclui a discussão dos cinco poliedros regulares, isto é, em que todas as faces são polígonos regulares iguais e com a mesma disposição em todos os vértices. Existem apenas cinco poliedros regulares, os cinco sólidos platónicos: tetraedro, cubo, octaedro, dodecaedro e icosaedro. A estes cinco poliedros, Platão associou os constituintes fundamentais da natureza — Fogo, Terra, Ar, Universo e Água — razão pela qual os poliedros regulares são também denominados sólidos platónicos.
Num icosaedro, as retas que passam por vértices opostos, as que passam pelos centros de faces opostas e as que passam pelos pontos médios de arestas opostas são, respetivamente, eixos de simetria rotacional de ordem 5, 3 e 2.

Com efeito, os eixos que passam por vértices opostos são de ordem 5 porque quando rodado o icosaedro de 360° em torno de cada um deles são necessárias 5 rotações de 72° para ele retomar a posição inicial. Quanto aos eixos que passam pelos centros de faces opostas, ao fim de 3 rotações de 120°, o icosaedro retoma a posição inicial e, para os eixos que passam pelos pontos médios, bastam 2 rotações de 180° para ele retomar a posição inicial.
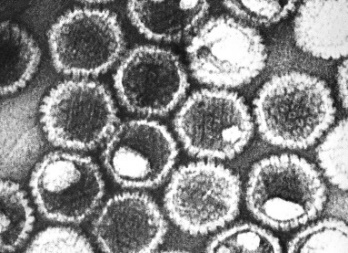
Muitos vírus, como o vírus causador do herpes, assumem uma simetria icosaédrica. As estruturas virais são constituídas de subunidades proteicas idênticas repetidas e o icosaedro é a forma mais simples de se montar tais subunidades. Esta estrutura maximiza o volume para armazenamento do material genético.
Neste tipo de vírus, múltiplas cópias de uma ou mais proteínas, distribuem-se segundo a simetria de um icosaedro. A organização das proteínas do capsídeo, segundo esta simetria, torna o processo de criação de novos vírus mais eficaz, uma vez que a formação de um capsídeo com esta forma recorre ao menor número e diversidade de proteínas.
Atendendo a que num icosaedro temos 20 triângulos e cada um tem 3 vértices, cada vértice está em contacto com 59 vértices. Assim, por cada proteína presente em determinado ponto, existem outras 59 relacionadas, o que aumenta a área de contacto do vírus com o seu alvo.
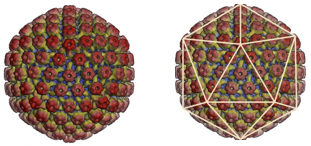
Uma vez reconhecida uma célula-alvo, o vírus quebra o seu capsídeo e introduz o material genético dentro da célula, que assume o controlo da mesma para se replicar continuamente. Esta replicação leva ao rebentamento da célula, migrando os novos vírus para as células vizinhas.
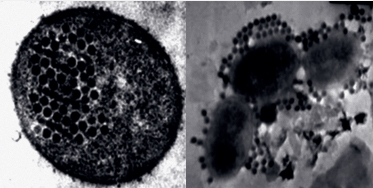
Também outros conceitos matemáticos, como as pavimentações, são utilizados para modelar a estrutura do capsídeo, indicando a posição e orientação relativa das suas proteínas.
No Modelo de Pavimentação do Vírus do Papiloma Humano (HPV), as interações entre três proteínas são representadas por ladrilhos em forma de papagaios de papel e as interações entre duas proteínas representadas por ladrilhos em forma de losangos.

A enorme influência dos vírus na vida humana, torna a investigação em virologia fundamental no desenvolvimento de novas terapias, para o que a informação sobre as características das estruturas virais é importante. O desenvolvimento e aplicação de métodos matemáticos fornece, assim, novas oportunidades para atingir este objetivo.
Também as técnicas computacionais permitem simular a configuração de muitos vírus e as imagens virtuais facilitam o estudo geométrico das suas estruturas.

Mas, antes do icosaedro ser descoberto nos vírus, os mesmos princípios foram aplicados pelo arquiteto Buckminster Fuller na construção de edifícios icosaédricos, as cúpulas geodésicas.

Em 1949, Fuller construiu a primeira cúpula geodésica. Tinha 4,3 metros de diâmetro e era feita de um tubo de alumínio e uma camada de vinil em forma de icosaedro.
Para demonstrar aos céticos a solidez da estrutura, Fuller pediu a vários alunos que o tinham ajudado na construção para, com ele, nela se suspenderem. O seu objetivo era construir uma estrutura de cúpula forte com economia de materiais. Observando que um triângulo era duas vezes mais forte do que um suporte quadrado, construiu uma cúpula apenas com triângulos. Esta opção usa menos material ao mesmo tempo que ajuda a maximizar o volume.

Em 1954, na Trienal de Milão, Fuller apresentou esta cúpula. Além de receber o gran premio, granjeou reconhecimento internacional. Este tipo de estrutura ganhou popularidade graças ao baixo impacto ambiental e durabilidade em todos os climas.

[editar] Referências
- D. C. TWAROCK R., Viruses and Geometry: Group, Graph and Tiling Theory Open Up Novel Avenues for Anti-Viral Therapy, London Mathematical Society Impact150 Stories, 1, pp. 63–68. 2016. DOI: 10.1112/i150lms/t.0005.
- https://www.vimat.pt/wp content/uploads/2020/02/paineis_biologia_matematica_compressed.pdf.
- https://issuu.com/s.c.williams-library/docs/de_divina_proportione.
- https://viruspatterns.com/.
- https://www.researchgate.net/publication/349013083_Models_of_viral_capsid_symmetry_as_a_driver_of_discove ry_in_virology_and_nanotechnolog.
- http://www.bubblemania.fr/architecture-bulle-dome-geodesique-inventeur-r-buckminster-fuller-1895-1983/.
- http://bubblemania.fr/wp-content/uploads/Dome_1949_K._Snelson_photo.jpg.
- http://bubblemania.fr/wp-content/uploads/105_10Lg.jpg.
Criada em 21 de Julho de 2022
Revista em 22 de Julho de 2022
Aceite pelo editor em 14 de Outubro de 2022

