Vibrações
Referência : Lage, E., (2020) Vibrações, Rev. Ciência Elem., V8(1):015
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2020.015]

Uma vibração é uma oscilação localizada, em geral, numa pequena região do espaço e efectuando-se em torno de um centro de equilíbrio. O seu modelo mais simples é o oscilador harmónico, com uma frequência própria bem definida, que se mostra capaz de uma boa descrição de vibrações moleculares, de simples circuitos eléctricos, etc.. A sobreposição de vibrações com diferentes frequências fundamenta fenómenos de interferência e batimento, e a consideração de vários osciladores harmónicos acoplados conduz ao importante conceito de modos normais de vibração, bem como à propagação das vibrações no espaço, um fenómeno que antecipa o conceito de onda.
Uma vibração harmónica é caracterizada pela sua amplitude (o máximo valor do afastamento do equilíbrio) e o período \(T\) (o tempo decorrido entre duas amplitudes consecutivas) ou a frequência \(\nu\) (o inverso do período, i.e., o número de amplitudes consecutivas observadas num segundo). A frequência angular \(\omega\) é, simplesmente, a frequência multiplicada por \(2\pi\).
Se aplicarmos duas forças, de frequências diferentes, a um oscilador harmónico (ver "Oscilador harmónico"), a resposta é a soma das respostas para cada uma das forças considerada isoladamente. O mesmo se passa num circuito LC, podendo aquela sobreposição ser facilmente implementado num laboratório.
Temos assim:
\(x(t)=a_{1}cos(w_{1}t)+a_{2}cos(w_{2}t+\phi )\)(1)
Aqui, \(a_{1}\) e \(a_{2}\) são as amplitudes do oscilador para cada uma das forças; \(\omega _{1}\) e \(\omega _{2}\) as respectivas frequências angulares; e \(\phi\) é a diferença de fase entre as duas vibrações, a qual será ignorada no que se segue. As amplitudes e diferença de fase são determinadas pela forma analítica das forças aplicadas, mas tal não interessa agora.
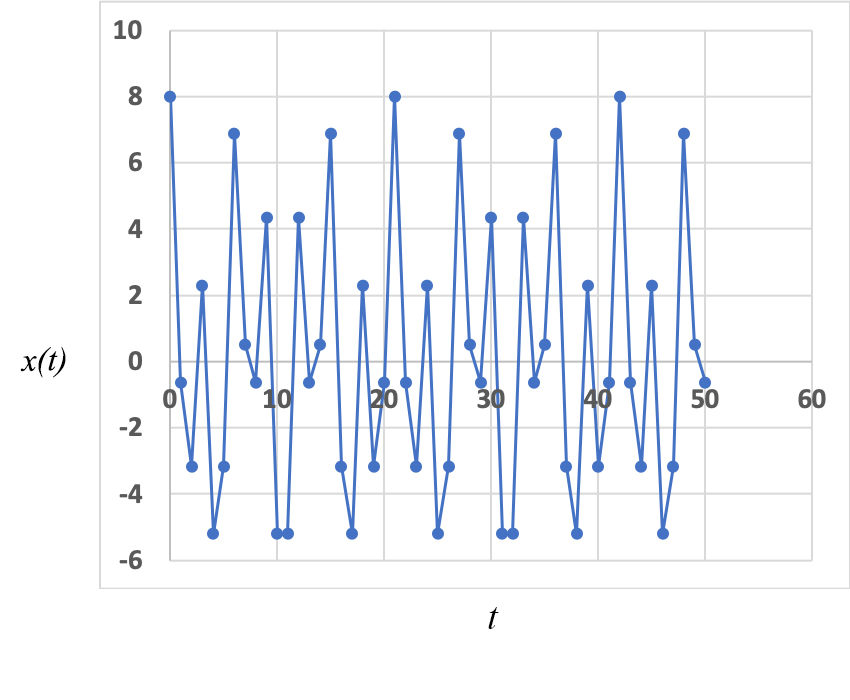
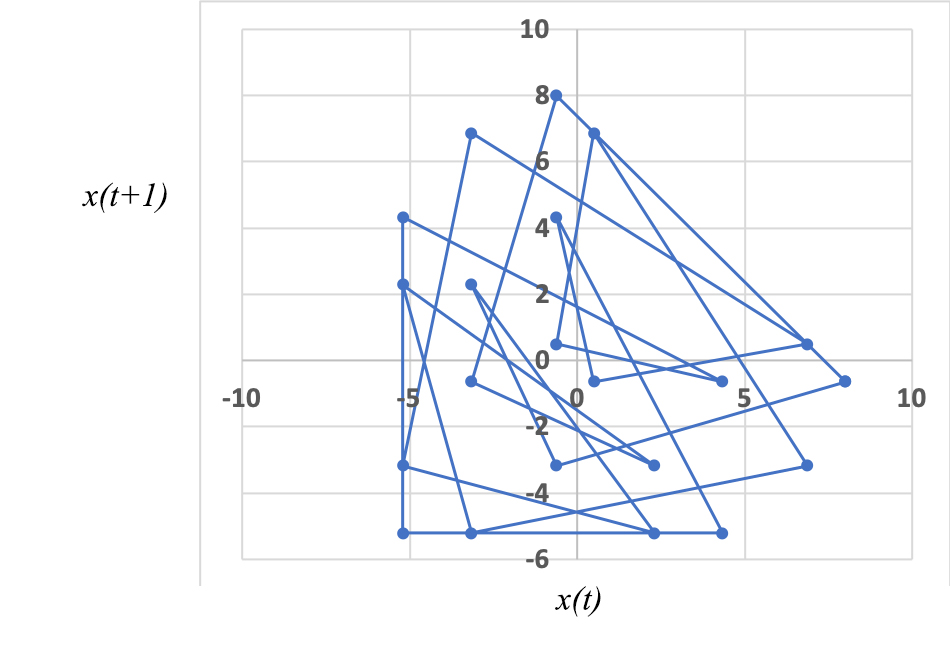
Um primeiro resultado interessante ocorre quando a razão \(\frac{\omega _{1}}{\omega _{2}}=\frac{T_{2}}{T_{1}}=\frac{\eta _{1}}{\eta _{2}}\) for um número racional (\(\eta _{1}\), \(\eta _{2}\) números naturais, primos entre si). Então, ao fim do tempo \(T=n_{1}T_{1}=n_{2}T_{2}\). Ambos os osciladores repetem os respectivos estados iniciais – a sobreposição destas vibrações é periódica, com o período \(T\) (FIGURA 1, onde \(a_{1}=5\), \(a_{2}=3\), \(T_{1}=3\), \(T_{2}=7\), resultando num período \(T=21\)). Uma outra maneira de tirar a mesma conclusão consiste em representar graficamente \(x(t+1)\), como ordenada, e \(x(t)\), como abcissa: obtém-se uma curva fechada, confirmando a periodicidade do sistema (FIGURA 2). (Este método pode ser aplicado a uma série de dados numéricos onde se suspeita haver comensurabilidade de períodos).
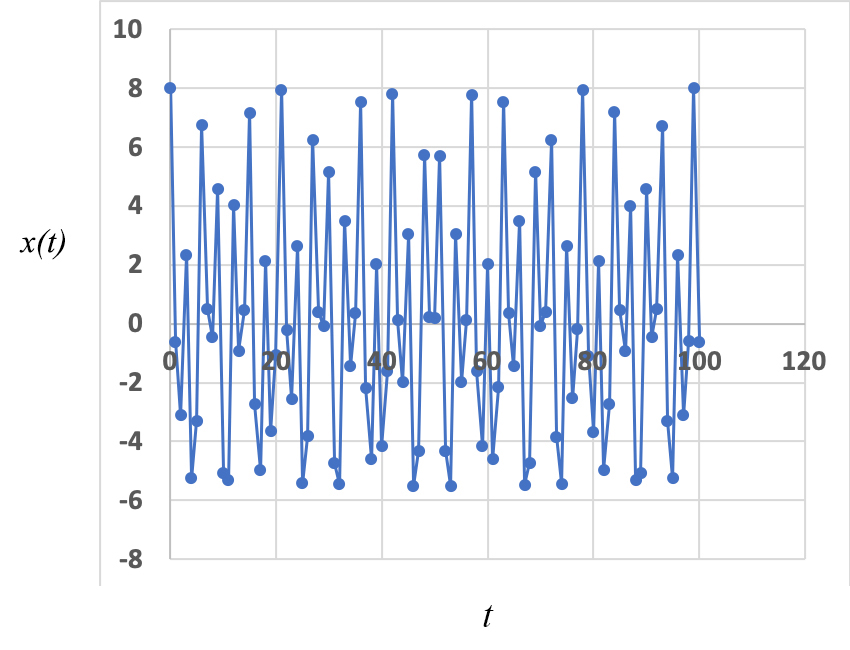
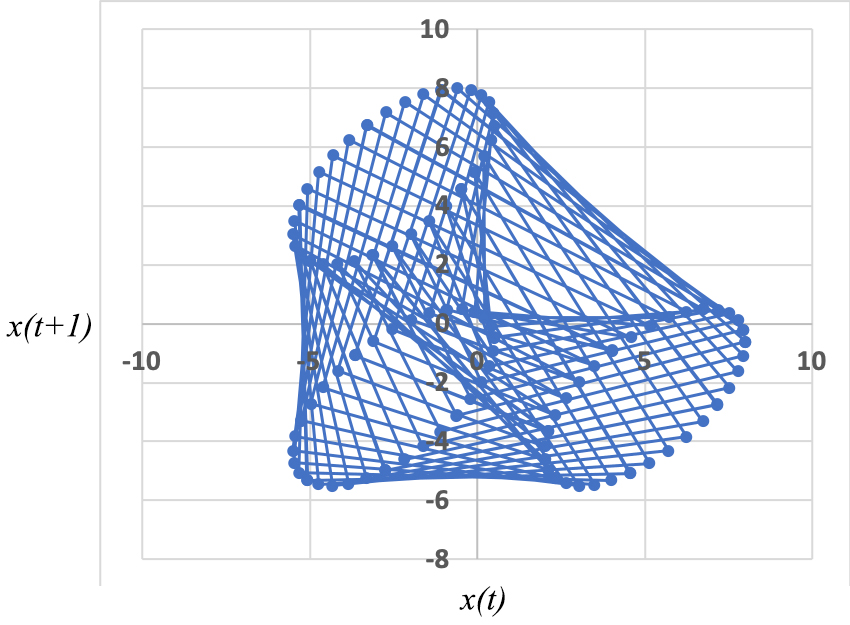
Situação muito diferente ocorre quando as duas frequências são incomensuráveis, i.e., \(\frac{\omega _{1}}{\omega _{1}}\) for um número irracional. Agora, não há repetição possível, embora possa, por vezes, parecer (FIGURA 3; amplitudes iguais às da FIGURA 1, \(T_{1}=3\), \(T_{2}=\sqrt{50}\)). A representação \(x(t+1)\) vs \(x(t)\) é elucidativa: em vez de uma curva fechada, encontra-se uma região densa, mostrando ser este um método expedito para exibir a incomensurabilidade dos períodos (FIGURA 4).
Um segundo resultado ocorre quando as duas frequências estão muito próximas. Suponhase, então, que \(\omega _{1}=\omega +\delta \omega \) e \(\omega _{2}=\omega -\delta \omega\), com \(\delta \omega \ll \omega\). A eq. (1) reescreve-se:
\(x(t)=\left \{ \left ( a_{1}+a_{2} \right )cos\left ( \delta \omega t \right ) \right \}cos\left ( \omega t \right )+\left \{ \left ( a_{1}-a_{2} \right )sen\left ( \delta \omega t \right ) \right \}sen\left ( wt \right )\)
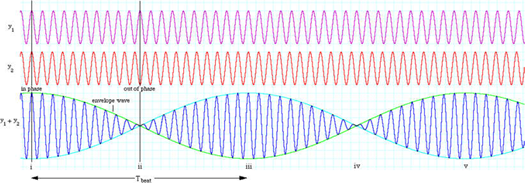
Os termos dentro das chavetas variam muito lentamente no tempo quando comparados com os factores que os multiplicam. Quer dizer, a vibração é quase sinusoidal, mas tem uma amplitude lentamente modulada no tempo (FIGURA 5). Trata-se do fenómeno de batimento que, por vezes, se experimenta ao sintonizar uma estação de rádio (em AM) com uma frequência muita próxima da frequência de outra estação.
Osciladores acoplados geram um novo tipo de vibrações conhecidas por modos normais de vibração. Na FIGURA 6A , os dois osciladores harmónicos (ambos com a mesma ‘constante da mola’ k) estão ligados por um potencial harmónico (constante k’). Os seus deslocamentos das posições de equilíbrio são designados por \(u_{1}\) e \(u_{2}\) , obtendo-se facilmente as equações de movimento(2):
\(m\frac{d^{2}u_{1}}{dt^{2}}=-ku_{1}+k'\left ( u_{2}-u_{1} \right )\)
\(m\frac{d^{2}u_{2}}{dt^{2}}=-ku_{2}-k'\left ( u_{2}-u_{1} \right )\) (2)
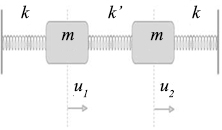
Os modos normais são as soluções harmónicas destas equações, sendo, neste caso, fáceis de encontrar explorando as simetrias do problema. Com efeito, designando por \(u\pm =u_{1}\pm u_{2}\), obtém-se, por soma e diferença das eqs.(2), as equações equivalentes:
\(m\frac{d^{2}u_{+}}{dt^{2}}=-ku_{+}\rightarrow \omega _{+}=\sqrt{\frac{k}{m}}\xrightarrow[ ]{u_{1}}\xrightarrow[ ]{u_{2}}\)
\(m\frac{d^{2}u_{-}}{dt^{2}}=-\left ( k+2k' \right )u_{-}\rightarrow \omega _{-}=\sqrt{\frac{k+2k'}{m}}\xrightarrow[ ]{u_{1}}\xleftarrow[ ]{u_{2}}\)
No modo simétrico \((u_{+})\), as duas massas deslocam-se em fase: a mola que as une está sempre relaxada; no modo anti-simétrico \((u_{-})\), as massas deslocam-se em anti-fase: a mola intermédia é comprimida, quando as massas se deslocam uma contra a outra, e é distendida, quando aquelas massas se afastam uma da outra, justificando por que \(\omega _{-}> \omega _{+}\). As setas acima indicam estes movimentos.
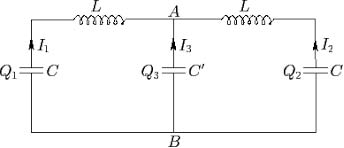
A FIGURA 6B representa um circuito elétrico (L, coeficiente de auto indução das bobines; C e C’ capacidades dos condensadores), para o qual as correntes de malha \(I_{1}\) e \(I_{2}\) satisfazem às mesmas eqs. (2), servindo, pois, como computador analógico do sistema mecânico considerado.
Numa molécula, a energia das interações atómicas tem mínimos que definem as posições de equilíbrio dos átomos. Pequenos afastamentos dos átomos originam um crescimento da energia quadrática nos deslocamentos como se os átomos estivessem ligados por molas. A procura dos modos normais de vibração da molécula é fundamental para determinar o respetivo espectro vibracional. A existência de simetrias ajuda a identificar estes modos, como se viu no exemplo anterior e se mostrará, a seguir, numa sua generalização de grande importância em Física do Estado Sólido.
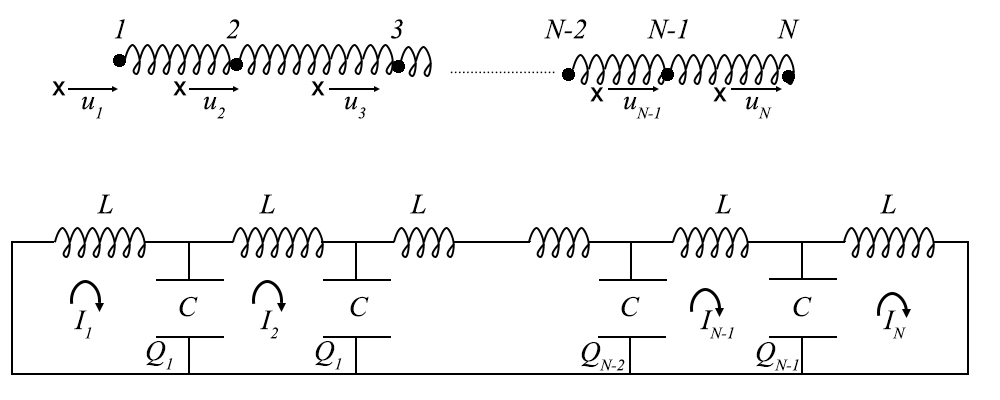
Considerem-se \(N\) osciladores harmónicos acoplados (FIGURA 7, em cima); seja \(u_{n}\left ( n=1,2,...,N \right )\) o deslocamento do oscilador n contado a partir da posição de equilíbrio (marcado com x, na FIGURA 7).
As equações de movimento ficam(3):
\(m\frac{d^{2}u_{1}}{dt^{2}}=k\left ( u_{2}-u_{1} \right )\)
\(m\frac{d^{2}u_{2}}{dt^{2}}=-k\left ( u_{2}-u_{1} \right )+k\left ( u_{3}-u_{2} \right )\)
\(...\)
\(m\frac{d^{2}u_{n}}{dt^{2}}=-k\left ( u_{n}-u_{n-1} \right )+k\left ( u_{n+1}-u_{n} \right )\)
\(...\)
\(m\frac{d^{2}u_{N-1}}{dt^{2}}=-k\left ( u_{N-1}-u_{N-2} \right )+k\left ( u_{N}-u_{N-1} \right )\)
\(m\frac{d^{2}u_{N}}{dt^{2}}=-k\left ( u_{N}-u_{N-1} \right )\)
É fácil verificar que:
\(\sum_{n=1}^{N}\frac{d^{2}u_{n}}{dt^{2}}=0\) (4)
porque não há forças exteriores. Consideremos, agora, as soluções que dependem do tempo como \(e^{-\omega x}\) - serão, por definição, os modos normais deste sistema. Obtém-se[1]>(5):
\(-m\omega ^{2}u_{1}=k\left ( u_{2}-u_{1} \right )\)
\(-m\omega ^{2}u_{2}=-k\left ( u_{2}-u_{1} \right )+k\left ( u_{3}-u_{2} \right )\)
\(...\)
\(-m\omega ^{2}u_{n}=-k\left ( u_{n}-u_{n-1} \right )+k\left ( u_{n+1}-u_{n} \right )\)
\(...\)
\(-m\omega ^{2}u_{N-1}=-k\left ( u_{N-1}-u_{N-2} \right )+k\left ( u_{N}-u_{N-1} \right )\)
\(-m\omega ^{2}u_{N}=-k\left ( u_{N}-u_{N-1} \right )\)
(Para evitar complicar a notação, representamos da mesma forma os deslocamentos, embora eles sejam reais em (3) e complexos em (5). Os deslocamentos reais obter-se-ão, no fim dos cálculos, tomando a parte real dos complexos após multiplicação pelo factor \(e^{-i\omega t}\)).
Excetuando os extremos \(\left ( n=1,n=N \right )\), observa-se uma simetria: a equação para a partícula \(n+1\) obtem-se da equação para a partícula n substituindo, simplesmente, \(n\) por \(n+1\). Tal sugere que se procurem soluções tais que \(\frac{u_{n}+1}{u_{n}}\) seja constante, mas essa constante só pode ter módulo 1, caso contrário haveria um crescimento dos deslocamentos para um dos lados.
Assim, será \(\frac{u_{n+1}}{u_{n}}=e^{iq}\) com \(q\) real, i.e., \(u_{n}\propto e^{iqn}\). Substituindo nas equações para \(n=2,...,N-1\), obtém-se:
\(-m\omega ^{2}=-k\left ( 1-e^{-iq} \right )+k\left ( e^{iq}-1 \right )\)(6)
Isto é:
\(\omega =\sqrt{\frac{2k}{m}\left ( 1-cosq \right )}\)(7)
Este resultado é conhecido por relação de dispersão. Notar-se-á que a substituição \(q\rightarrow -q\) conduz à mesma relação de dispersão. Assim, a solução geral, para um dado \(q\), é:
\(u_{n}=e^{-\omega _{q}t}\left [ A_{q}e^{iqn}+A_{-q}e^{-iqn} \right ]\)(8)
onde \(\omega_{q}\) é definido pela eq.(7), e \(A_{\pm q}\) são constantes (complexas). A eq. (8) tem uma interpretação simples: o deslocamento é a sobreposição de uma vibração que se propaga para a direita \((A_{q})\) com outra que se propaga para a esquerda \((A_{-q})\). Com efeito, considerando, apenas, o termo de amplitude \(A_{q}\), é fácil verificar que \(u_{n+1}\left ( t+\tau \right )=u_{n}\left ( t \right )\) com \(\omega \tau =q\). Análise idêntica pode ser efetuada para o modo de amplitude \(A_{-q}\). Quais os valores possíveis para \(q\)? Para começar, notar-se-á que a substituição \(q\rightarrow q+2\pi\) dá os mesmos deslocamentos. Assim, \(q\) pode restringir-se a um intervalo de amplitude \(2\pi\), sendo habitual considerar o intervalo \(\left . \right ]-\pi, \pi \left . \right ]\), conhecido por 1ª zona de Brillouin. Contudo, nas expressões anteriores, consideraram-se explicitamente as contribuições de \(q\) e \(–q\), pelo que \(q\epsilon \left [ 0,\pi \right ]\) com \(-q\) a completar o resto da zona de Brillouin. Depois, substituindo qualquer das componentes da eq. (8) na eq. (4), obtém-se
\(\sum_{n=1}^{N}e^{\pm iqn}=0\rightarrow e^{\pm iqN}=1\rightarrow q=\frac{2\pi l}{N}l\)\(l=0,1,...,\frac{N-1}{2},I\)(9)
\(I(x)\) é o maior inteiro menor ou igual a \(x\). Note-se que \(q=0\), embora permitido, é muitas vezes omitido porque corresponde a uma translação uniforme de todas as massas
A FIGURA 8 representa a relação de dispersão, eq. (7). Os valores de q distribuem-se igualmente espaçados no eixo horizontal: o seu conjunto torna-se denso para \(N\gg 1\). Observe-se que, para pequenos valores de \(\left | q \right |\), tem-se:
\(\omega _{q}=\sqrt{\frac{k}{m}}\left | q \right |\)(10)
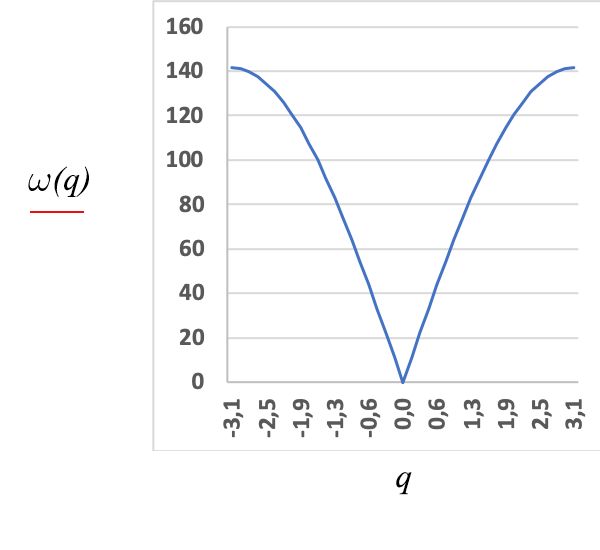
Mostrar-se-á, adiante, o significado desta expressão.
Finalmente, considerem-se as eqs. (5) para os extremos, \(n=1\) e \(n=N\). Inserindo a solução encontrada, eq. (8), substituindo \(m\omega ^{2}\) através da eq. (6) e lembrando ser \(e^{\pm iqN}=1\), obtem-se, para ambos os extremos, o mesmo resultado:
\(A_{q}\left ( e^{iq}-1 \right )+A_{-q}\left ( e^{-iq}-1 \right )=0\rightarrow \frac{A_{-q}}{A_{q}}=e^{iq}\)(11)
Assim, definindo \(A_{\pm q}\equiv \frac{a_{q}}{2}e^{\mp i\frac{q}{2}}\), inserindo na eq. (8), tem-se:
\(u_{n}=a_{q}e^{-i\omega _{q}t}cos\left ( q\left ( n-\frac{1}{2} \right ) \right )\)
A solução geral das equações de movimento é, então:
\(u_{n}(t)=Re\left [ \sum_{q}^{ }a_{q}e^{-i\omega _{q}t}cos\left ( q\left ( n-\frac{1}{2} \right ) \right ) \right ]\)(12)
sendo a soma efectuada sobre os valores permitidos em (9).
O leitor, certamente, terá tido a dúvida: se, por exemplo, a partícula 1 estiver presa, como se determinam os valores de q? Agora, a equação, em (3), para a partícula 1, terá um termo adicional da força que a prende, o que invalida a conclusão expressa na eq. (4). Contudo, há, agora, a condição \(u_{1}\equiv 0\) que se exprime na relação \(\frac{A_{-q}}{A_{q}}=e^{2iq+i\pi}\). E tem-se a equação para \(n=N\), em (5), o que fornece outra relação para \(\frac{A_{-q}}{A_{q}}\). A compatibilidade entre estas duas equações fornece os valores possíveis para \(q\) (no caso \(e^{iq(2N-1)+ix}=1\)). Da mesma forma se procederia se os dois extremos estivessem fixos.
Quando \(N\gg 1\), mas a cadeia de osciladores mantem, no equilíbrio, um tamanho finito \(L\), a cadeia aparece como um fio contínuo e deformável. Seja \(a\) a distância entre as posições de equilíbrio. Então, \(L=(N-1)\) a e a massa da cadeia é \(M=Na\), apresentando, assim, no equilíbrio, uma densidade (massa por unidade de comprimento) \(\rho =\frac{M}{L}=\frac{Nm}{\left ( N-1 \right )a}\simeq \frac{m}{a}\).
Imagine-se, agora, que a partícula 1 está fixa na sua posição de equilíbrio e que é aplicada uma força externa \(F\) na partícula \(N\). Atingido um novo equilíbrio, a cadeia aumentou o seu comprimento \(L\rightarrow L+\delta L\), com \(\delta L=u_{N}\). Voltando às eqs. (3), esta situação estática é descrita igualando a 0 os primeiros membros e acrescentado a força F à última equação. É fácil encontrar os deslocamentos: \(u_{n}=\left ( n-1 \right )\frac{F}{k}\), pelo que:
\(\frac{\delta L}{L}=\frac{u_{N}}{\left ( N-1 \right )a}=\frac{F}{ka}\)
Esta é uma forma da lei de Hooke: identificamos, assim, \(ka\) com o módulo de Young \((E)\) adaptado a este modelo unidimensional de um sólido.
Observado de longe, o sistema de osciladores aparece como um fio contínuo cujas oscilações são descritas por um campo de deslocamentos \(u(x,t)\)(ver "Campos"). A relação deste campo com os deslocamentos dos osciladores é: \(\left [ u\left ( x,t \right ) \right ]_{x=na}=u_{n}\left ( t \right )\). Considerando a equação de movimento deste oscilador (ver. (3)), podemos reescreve-la sob a forma:
\(m\left [ \frac{\partial ^{2}u\left ( x,t \right )}{\partial t^{2}} \right ]_{x=na}=k\left [ u\left ( x+a,t \right )+u\left ( x-a,t \right )-2u\left ( x,t \right ) \right ]_{x=na}\)
No limite \(a\rightarrow 0\), com \(x=na\) fixo, este segundo membro pode desenvolver-se até à segunda ordem, obtendo-se:
\(m\left [ \frac{\partial ^{2}u\left ( x,t \right )}{\partial t^{2}} \right ]_{x=na}=ka^{2}\left [ \frac{\partial ^{2}u\left ( x,t \right )}{\partial x^{2}} \right ]_{x=na}\)
A referência à posição \(x=na\) é, agora, irrelevante. E usando os resultados anteriores para a densidade e módulo de Young, tem-se:
\(\rho \frac{\partial ^{2}u\left ( x,t \right )}{\partial t^{2}}=E\frac{\partial ^{2}u\left ( x,t \right )}{\partial x^{2}}\)
Esta é a equação de onda a uma dimensão que merece um tratamento autónomo. Como se verá, ela prevê que ondas elásticas se propaguem com a velocidade \(c_{s}=\sqrt{\frac{E}{\rho }}\). Ora, na parte linear da relação de dispersão atrás obtida, encontrou-se (eq. (10)) \(\omega _{q}=\sqrt{\frac{k}{m}}\left | q \right |\)
Eliminando \(k\) e \(m\) em favor do módulo de Young e densidade, como atrás se mostrou, podemos reescrever:
\(\omega _{q}=\sqrt{\frac{E}{\rho }}\frac{\left | q \right |}{a}\)
Identifica-se, assim, \(\frac{q}{a}\) com o vector de onda. O resultado mostra que a parte linear da relação de dispersão é, afinal, a relação linear entre frequência e vector de onda como explicado na Ref. 2.
Idênticas considerações podem ser adaptadas à rede de circuitos \(LC\) exibida na FIGURA 7. No limite do contínuo, aquela rede identifica-se com uma linha de transmissão de electricidade.
[editar] Referências
- LAGE, E. Ondas, Rev. Ciência Elem., V8(1):016. (2020). DOI: 10.24927/rce2020.016.
- The Feynman Lectures on Physics, Volume 1, ISBN: 9780465024933. 1964.
- LAGE, E. O oscilador harmónico, Rev. Ciência Elem., V7(2):033. (2019). DOI: 10.24927/rce2019.033.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 17 de Outubro de 2019
Revista em 17 de Fevereiro de 2020
Aceite pelo editor em 28 de Fevereiro de 2020

