Referência : Nápoles, S., (2018) Sobre o volume de troncos, Rev. Ciência Elem., V6(1):003
Autora: Suzana Nápoles
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2018.003]

Geometricamente, um tronco de um sólido é a porção do sólido compreendida entre dois planos paralelos que o seccionam, por exemplo um tronco de pirâmide ou de cone. Se a utilização de troncos de pirâmide na construção remonta ao terceiro milénio antes de Cristo, os troncos de cone são parte integrante de projetos arquitetónicos no segundo milénio depois de Cristo.

Datam de cerca de 3 100 a.C. as mastabas, edifícios funerários egípcios em forma de troncos de pirâmide com base retangular.

FIGURA 1. Pirâmide de Djoser em Saqqara, Egito.

Entre 2 700 e 2 600 a.C. as mastabas deram origem a pirâmides em degraus, a primeira das quais foi a pirâmide de Djoser em Saqqara (FIGURA 1). As pirâmides de faces lisas surgem entre 2 573 e 2 454 a.C..

FIGURA 2. Pirâmide do Sol em Teotihuacan, México.

A pirâmide do Sol em Teotihuacan, cuja construção foi concluída cerca de 200 d.C., é composta por troncos de pirâmides quadrangulares (FIGURA 2).

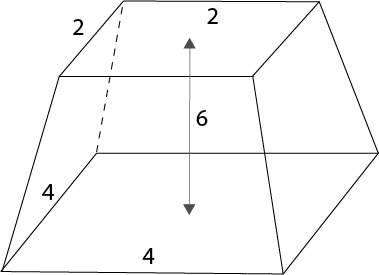
No Papiro de Moscovo, cuja origem remonta a 1 850 a.C., é tratado o volume de um tronco de pirâmide. Este papiro contém 25 problemas com soluções, 7 dos quais são problemas geométricos. Entre eles, o Problema 14 diz respeito à determinação do volume de um tronco obtido truncando uma pirâmide quadrangular de tal forma que o topo é um quadrado cujo lado mede duas unidades de comprimento, a base é um quadrado cujo lado mede quatro unidades de comprimento e a distância entre as bases é igual a 6 unidades de comprimento.

Problema 14

“Se te disserem: Uma pirâmide truncada tendo 6 como altura vertical 4 na base e 2 no topo: Deves calcular o quadrado de 4; resulta 16. Deves duplicar 4; resulta 8. Deves calcular o quadrado de 2; resulta 4. Deves somar 16, 8 e 4; resulta 28. Deves tomar 1/3 de 6; resulta 2. Deves tomar 28 duas vezes; resulta 56.”

Esta solução parece evidenciar que os egípcios conheciam a fórmula para determinar o volume do tronco de uma pirâmide quadrangular,\(V=\frac{1}{3}h(a^2+ab+b^2)\) , mas esta fórmula não está neste papiro.

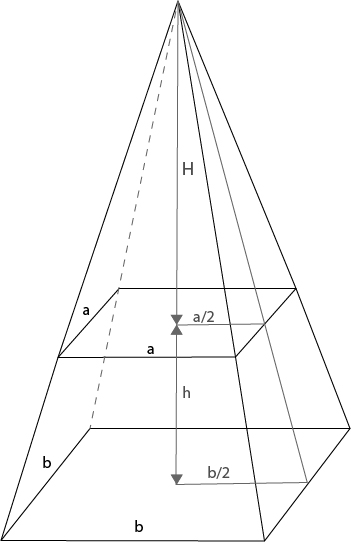
Para a deduzir, basta recorrer à diferença dos volumes de duas pirâmides, como se indica na figura.

Com efeito, tendo em conta que

\(\frac{H}{a/2}=\frac{H+h}{b/2}\Leftrightarrow H=\frac{a}{b-a}h,\)

o volume V do tronco da pirâmide é dado por

\(v=\frac{1}{3}b^2(H+h)-\frac{1}{3}a^2 H\)

\(=\frac{1}{3} h \frac{b^3}{b-a}-\frac{1}{3}h\frac{a^3}{b-a}=\frac{1}{3}h(a^2+ab+b^2)\)

O fuste das colunas gregas, isto é, a porção de coluna compreendida entre a base e o capitel, pode ser composto por um só bloco (monolítico) ou composto pela sobreposição de diversos blocos designados em arquitetura por tambores.

FIGURA 3. Ruínas de Paestum, Grécia. (fonte: https://commons.wikimedia.org/w/index.php?curid=32408482)

Nas ruínas de Paestum (FIGURA 3), uma cidade grega situada na costa do Mar Tirreno e fundada no século VII a.C., destacam-se templos gregos cujas colunas são constituídas por tambores.

Estes tambores têm caneluras com arestas vivas pelo que, geometricamente, os podemos interpretar como troncos de pirâmide.

Genericamente, o volume de um tronco de qualquer pirâmide, tendo topo e base com áreas A₁ e A₂ e altura h, é dado por

\(V=\frac{1}{3}h(A_{1}+\sqrt{A_{1}A_{2}}+A_{2}).\)

Com efeito, uma vez que as pirâmides de altura H e H+h são semelhantes, tem-se que \(\frac{A_1}{A_2}= \left(\frac{H}{H+h}\right)^2.\)

Então, \(H=\frac {h\sqrt{A_{1}}}{\sqrt{A_{2}}-\sqrt{A_{1}}},H+h= \frac {h\sqrt{A_{2}}}{\sqrt{A_{2}}-\sqrt{A_{1}}}\) e

\(V=\frac{1}{3}(A_{2}(H+h)-A_{1}H)=\frac{1}{3}h\frac{\sqrt{A_{2}}A_{2}-\sqrt{A_{1}}A_{1}}{\sqrt{A_{2}}-\sqrt{A_{1}}}=\frac{1}{3}h(A_{1}+\sqrt{A_{1}A_{2}}+A_{2}).\)

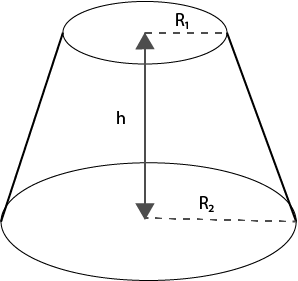
Esta fórmula adapta-se facilmente ao cálculo do volume do tronco de um cone circular reto de altura h, conhecidos os raios das duas bases.

Basta ter em conta que, neste caso, \(A_1=\pi R_1^2\) e \(A_2=\pi R_2^2\) pelo que

\(V=\frac{1}{3}h(\pi R_1^2+\sqrt{\pi R_1^2\pi R_2^2}+\pi R_2^2)=\frac{1}{3}\pi h(R_1^2+R_1R_2+R_2^2).\)

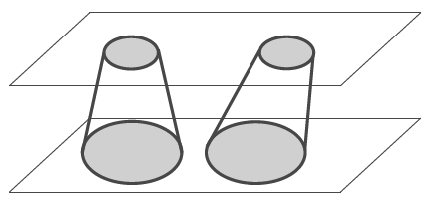
Pelo Princípio de Cavalieri, estas fórmulas mantêm-se verdadeiras para troncos de pirâmides não retas ou de cones não retos.

Se dois sólidos estão contidos entre um par de planos paralelos e qualquer plano paralelo àqueles, que interseta os sólidos, o faz em secções de corte com a mesma área então os dois sólidos têm o mesmo volume.

Das mastabas egípcias e dos tambores das colunas gregas até aos nossos dias, os troncos de pirâmides e cones continuam a marcar presença, tanto no design de peças de uso comum, como na arquitetura de edifícios.

Estas superfícies são regradas, isto é, por cada um dos seus pontos passa pelo menos uma reta nela contida.

A sua construção, ao proporcionar vantagens técnicas consideráveis, permite a realização de formas arquitetónicas arrojadas.

http://www.brasilengenharia.com	https://en.wikipedia.org/wiki/Tadao_Ando
https://en.wikipedia.org/wiki/The_Pyramids	https://pt.wikipedia.org/wiki/Teatro_Nacional_Cláudio_Santoro
https://frank.itlab.us/photo_essays/wrapper.php?feb_25_2008_calatrava.html