Semelhança de triângulos

Referência : Tavares, J.N., Geraldo, A., (2015) Semelhança de triângulos, Rev. Ciência Elem., V3(1):015
Autores: João Nuno Tavares e Ângela Geraldo
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.015]

Índice

Na figura 1 podemos ver uma correspondência entre os vértices de dois triângulos no plano, $\left[ABC\right]$ e $\left[A'B'C'\right]$ . Esta faz corresponder os pontos $A$ , $B$ e $C$ aos pontos $A'$ , $B'$ e $C'$ , respetivamente, assim como os ângulos $\alpha$ , $\beta$ e $\gamma$ aos ângulos $\alpha'$ , $\beta'$ e $\gamma'$ , respetivamente. Dizemos que dois triângulos são semelhantes se essa correspondência entre os vértices for de tal modo que: os ângulos correspondentes são geometricamente iguais; e os lados correspondentes são diretamente proporcionais, ou seja, $\frac{\overline{AB}}{\overline{A'B'}} = \frac{\overline{AC}}{\overline{A'C'}} = \frac{\overline{BC}}{\overline{B'C'}}$ . Nota - os lados de dois triângulos são proporcionais se existir proporcionalidade direta entre os seus comprimentos, ou seja, se o quociente entre os comprimentos dos lados correspondentes dos triângulos for sempre constante.

Dois quaisquer triângulos são semelhantes se tiverem dois ângulos correspondentes geometricamente iguais (o terceiro ângulo é necessariamente igual, pois a soma dos ângulos internos de um triângulo é sempre igual a 180°). Mova os pontos A, B ou C para alterar as amplitudes dos ângulos internos do triângulo. Ao mover o ponto A' obterá vários triângulos semelhantes a $\left[ABC\right]$ .

		Dois quaisquer triângulos são semelhantes se tiverem dois lados correspondentes diretamente proporcionais e o ângulo por eles formado for igual. Mova os pontos A, B ou C para alterar a amplitude do ângulo. Ao mover o ponto B' obterá vários triângulos semelhantes a $\left[ABC\right]$ .

Dois quaisquer triângulos são semelhantes se tiverem os três lados correspondentes diretamente proporcionais. Mova os pontos A, B ou C para alterar os comprimentos dos lados do triângulo. Verifique que os lados correspondentes são diretamente proporcionais. Ao mover o ponto A' obterá vários triângulos semelhantes a $\left[ABC\right]$ .

Criada em 12 de Novembro de 2012
Revista em 08 de Março de 2013
Aceite pelo editor em 08 de Março de 2013
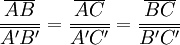