Pressão de vapor

Da WikiCiências
Share/Save/Bookmark
Ir para: navegação, pesquisa

Referência : Monte, M.J., (2018) Pressão de vapor, Rev. Ciência Elem., V6(3):053
Autor: Manuel João dos Santos Monte
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2018.053]
PDF Download


Vapor é um gás com potencial para ser condensado (liquefeito ou solidificado como um cristal) por aumento de pressão, ou seja, é um gás que se encontra a uma temperatura inferior à sua temperatura crítica. Esta é uma definição meramente técnica, uma vez que não há qualquer outra diferença entre gás e vapor.


A pressão exercida pelo vapor de uma substância pura em equilíbrio termodinâmico com uma das suas fases condensadas (cristalina ou líquida), a uma determinada temperatura, ou com ambas as fases, à temperatura do ponto triplo, designa-se por pressão de vapor. Seja \(A\) uma substância pura em equilíbrio com uma das suas fases condensadas (cristalina, \(cr\), ou líquida, \(l\)) à temperatura \(T\), num sistema fechado (sistema em que a quantidade total de \(A\) se mantém constante).


\(A(cr\), ou \(l) ⇔ A(g)\)


Por equilíbrio, deve entender-se que, por unidade de tempo, o número de moléculas de A que abandonam a fase condensada iguala o número de moléculas de \(A\) que condensam ao chocar com a superfície daquela fase. Por outro lado, o número de moléculas em fase gasosa por unidade de volume aumenta com a temperatura até se atingir a temperatura crítica, \(T_c\), e a pressão crítica de equilíbrio, \(p_c\).

A FIGURA 1 representa um diagrama de fases, com as zonas de sólido \(s\), líquido \(l\), gás (\(g\)), para a hipotética substância \(A\). As três linhas visíveis no diagrama são linhas de equilíbrio bifásico: cristal-líquido (fusão); líquido-gás (vaporização); cristal-gás (sublimação). Seja um sistema fechado onde existe apenas a substância A na fase cristalina em equilíbrio com o seu vapor à temperatura \(T_1\). A esta temperatura a pressão de vapor será \(p(T_1)\). Por aquecimento lento (para que o sistema permaneça sempre em equilíbrio) até à temperatura do ponto triplo a pressão de vapor aumenta até atingir o valor \(p_{Tr}\). Neste ponto começa a aparecer a fase líquida e as três fases estão em equilíbrio. O equilíbrio será desfeito, devido ao contínuo aquecimento, com a fusão total da fase cristalina. Note-se que enquanto durar este processo de fusão a temperatura manter-se-á constante, \(T_{Tr}\). Se o líquido resultante continuar a ser aquecido, a temperatura continuará depois a aumentar. À temperatura \(T_2\), a pressão de vapor será \(p(T_2)\).


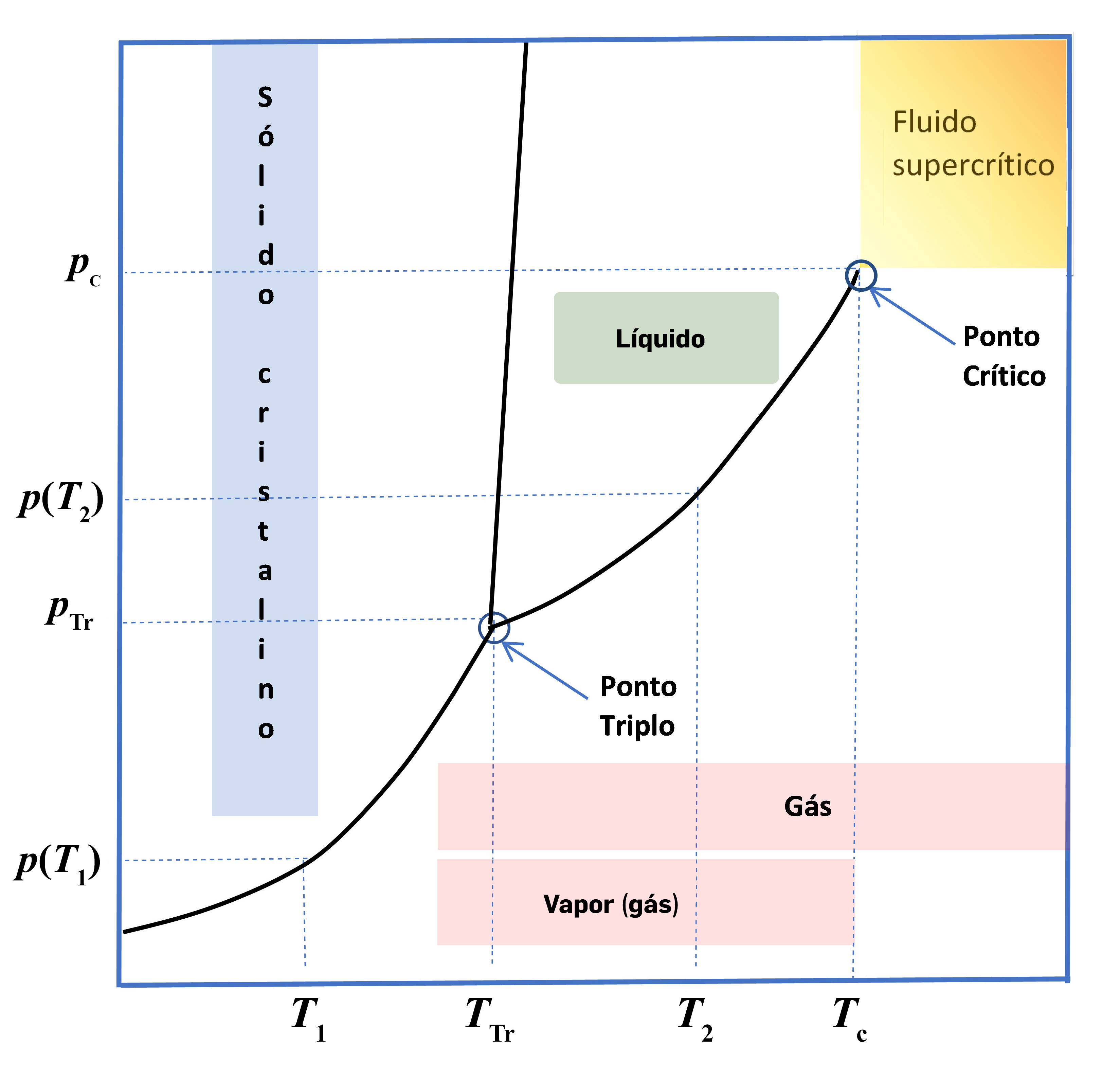
FIGURA 1. Diagrama de fases típico para uma substância pura.

De referir que durante o processo de aquecimento a densidade do vapor vai aumentando drasticamente, igualando a densidade do líquido ao atingir a temperatura crítica – último ponto da linha do equilíbrio de vaporização – em que deixa de haver distinção entre as duas fases (FIGURA 2). A partir daqui, por aumento de temperatura e de pressão o sistema manter-se-á num estado designado de fluido supercrítico.


FIGURA 2. Ilustração do equilíbrio fase condensada (a cheio) - fase gasosa, a duas temperaturas diferentes, de acordo com o diagrama representado na figura 1. O terceiro esquema representa o fluido supercrítico à temperatura \(T_c\).

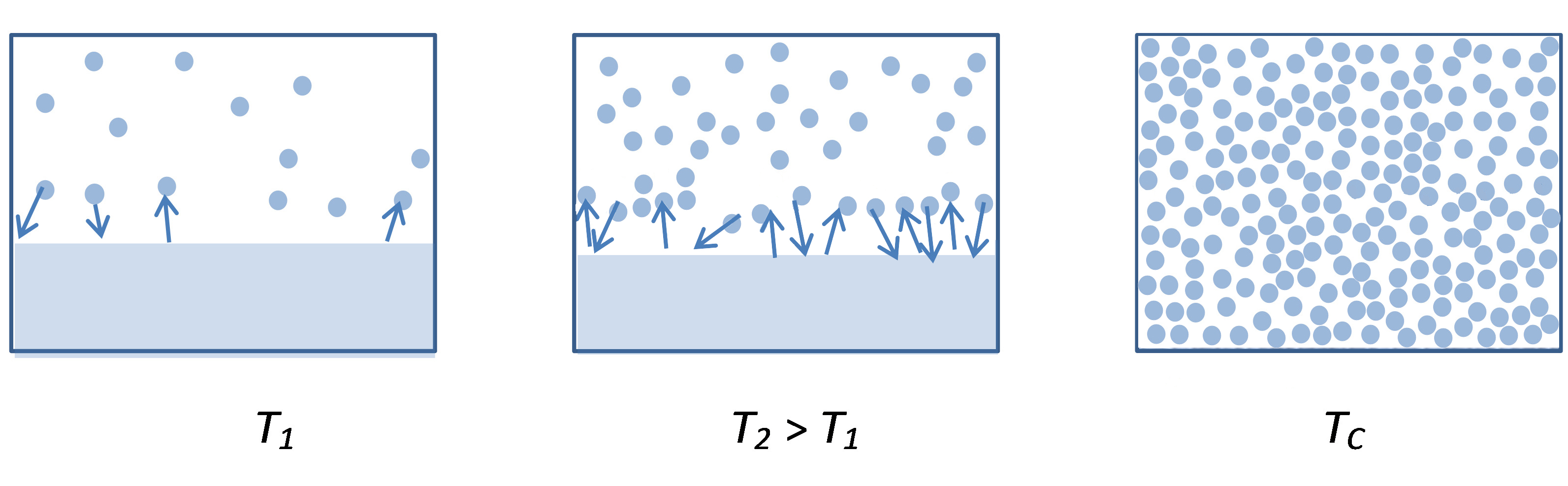
As funções termodinâmicas de sublimação ou vaporização

A energia de Gibbs molar de sublimação ou de vaporização, à pressão de referência \(p^o\), \(\Delta_{cr,l}^{g}G_{m}^{o}(T)\), é o potencial termodinâmico adequado para avaliar a volatilidade de uma substância pura, ou seja, a sua tendência para passar à fase gasosa. Para os não iniciados, a simbologia termodinâmica, pode parecer esotérica. Mas é simples e lógica. O símbolo \(\Delta_{cr,l}^{g}G_{m}^{o}(T)\), por exemplo, é a forma mais económica de referir “a diferença (Δ) entre a energia de Gibbs molar da fase gasosa e da fase condensada (cristalina ou líquida), à pressão de referência \(p^o\) e à temperatura \(T’’\).

Atendendo a que a energia de Gibbs molar de uma substância pura se identifica com o potencial químico (\(μ\)) dessa substância, a energia de Gibbs molar de sublimação ou de vaporização representa a diferença entre o potencial químico de \(A\) em fase gasosa e o seu potencial em fase condensada. À temperatura \(T\) será mais estável a fase com menor potencial químico. Esta diferença de potencial, \(\Delta_{cr,l}^{g}G_{m}^{o}(T)\), está relacionada com a pressão de vapor àquela temperatura, \(p(T)\), através da equação (1), onde \(R\) é a constante dos gases ideais.


\(\Delta_{cr,l}^{g}G_{m}^{o}(T)=-RT \ln \left[p(T)/p^o\right]\)            (1)


A pressão de referência po (geralmente unitária, por exemplo 1 Pa), que integra a equação (1), identifica as unidades da pressão \(p(T)\) (leia-se a pressão de vapor à temperatura \(T\)) sem prejudicar o formalismo que impõe que seja adimensional o argumento do logaritmo. À pressão de referência \(p^o\) e à temperatura \(T\), a fase condensada será tanto mais estável (menos volátil) quanto maior for o valor de \(\Delta_{cr,l}^{g}G_{m}^{o}(T)\) e, consequentemente, quanto menor for a sua pressão de vapor, \(p(T)\). Essa estabilidade da fase condensada depende de fatores entálpicos (associados às energias de ligação intermoleculares, que caracterizam apenas essa fase uma vez que para um gás ideal as interações intermoleculares são nulas) e de fatores entrópicos (associados à entropia quer da fase condensada quer da fase gasosa), de acordo com as equações (2) e (3). Nestas equações, \(\Delta_{cr,l}^{g}H_{m}^{o}(T)\), ainda frequentemente designado calor latente, representa a entalpia molar de sublimação ou de vaporização (endotérmica), sendo \(\Delta_{cr,l}^{g}S_{m}^{o}(T)\) a entropia molar dessa transição de fase, também sempre positiva.


\(\Delta_{cr,l}^{g}G_{m}^{o}(T)=\Delta_{cr,l}^{g}H_{m}^{o}(T)-T\Delta_{cr,l}^{g}S_{m}^{o}(T),\)            (2)


Combinando as equações (1) e (2) obtém-se a equação (3)


\(R\ln\left[p(T)/p^o\right]=\Delta_{cr,l}^{g}S_{m}^{o}(T)-\frac{\Delta_{cr,l}^{g}H_{m}^{o}(T)}{T}\)            (3)


Das equações anteriores conclui-se que no equilíbrio à pressão \(p(T) = p^o\), será \(\Delta_{cr,l}^{g}G_{m}(T)=0\) e \(\Delta_{cr,l}^{g}S_{m}(T)=\Delta_{cr,l}^{g}H_{m}(T)/T\).

Atingido o equilíbrio à temperatura \(T\), em sistema fechado, a quantidade de moléculas presentes em cada fase permanece constante. Em sistema aberto o processo de migração das moléculas para a fase gasosa continuaria até o eventual esgotamento da fase condensada, pois haveria um défice de moléculas da fase gasosa de \(A\), ou seja, a pressão exercida pelo vapor de \(A\) seria sempre inferior à sua pressão de vapor àquela temperatura. Estes dois tipos de comportamento fundamentam os princípios de duas classes de métodos de medição de pressões de vapor: medição em sistema fechado (métodos estáticos) e medição em sistema aberto (métodos dinâmicos). Enquanto nos métodos estáticos as determinações da pressão de vapor são realizadas em condições de equilíbrio, nos métodos dinâmicos procura-se criar condições experimentais de quasi-equilíbrio por forma a que a pressão do vapor à superfície da fase condensada possa ser considerada igual à pressão de vapor. Para compostos de reduzida volatilidade, os métodos estáticos que estão a ser mais utilizados atualmente incluem manómetros de capacitância muito sensíveis[1], enquanto nos métodos dinâmicos estão incluídos métodos de efusão (sendo o mais usado o de efusão de Knudsen[2]) e métodos de transpiração (também designados por “saturação de gás”[3]).



A variação da pressão de vapor com a temperatura

As primeiras equações

Em 1761, Joseph Black (1728-1799) observou que o calor fornecido durante a fusão do gelo, ou da vaporização da água, não provocava o aumento da temperatura destes sistemas em equilíbrio (respetivamente, gelo-água líquida ou água líquida – vapor de água). Black argumentou que durante estes processos, o calor (que na altura era interpretado como um fluido, o calórico), se combinava com as partículas de água permanecendo num estado latente durante a transição de fase, contrariamente ao calor sensível que, ao ser fornecido a um corpo, provocava aumento da sua temperatura[4]. A teoria do calor latente de Black é geralmente considerada um marco precursor da Termodinâmica. O equivalente atual à designação calor latente, que ainda é utilizada em algumas áreas da ciência fora da Termodinâmica, é a função entalpia (de fusão, sublimação ou vaporização) da qual depende, como mais tarde se descobriria, a taxa de variação da pressão de vapor com a temperatura.

John Dalton (1766-1844) é especialmente conhecido pelas leis das proporções múltiplas e das pressões parciais e também pela sua primordial contribuição para o desenvolvimentos da Teoria atómica[5]. Mas não está tão divulgado o seu interesse pela meteorologia que o motivou a medir pressões de vapor da água (quer misturada no ar, quer quando pura)[6]. Das suas experiências, Dalton concluiu que a humidificação do ar provocada pela evaporação de água só dependia da temperatura, sendo independente da presença de outros gases, ou seja, da pressão total. Além desta importante conclusão, devem-se a Dalton as primeiras medições “satisfatórias” de pressões de vapor, não só da água mas também de outros líquidos (éter, amoníaco, mercúrio, etc.), apesar da instrumentação artesanal que utilizava. Em 1805, Dalton publicou aquela que pode ser considerada a primeira equação de pressão de vapor (Eq. 4), que previa um aumento exponencial da pressão de vapor com a temperatura[7].


\(p = p^oa^{(t/ºC)}\)            (4)


Apesar de rudimentar, a equação (4) serviu de ponto de partida para o desenvolvimento de novas equações que iam sendo aperfeiçoadas à medida que mais determinações experimentais eram conhecidas. Entre elas, destacam-se equações propostas por Jean-Baptiste Biot (1774-1862)[8], [9] e por Henri Regnault (1810-1878)[10], [11].


Clapeyron e Clausius

Em 1834[12], Benoit-Pierre-Emile Clapeyron (1799–1864) derivou a primeira equação de pressão de vapor que incluía como parâmetro o calor latente de Black. Na época, a noção de temperatura absoluta era ainda desconhecida, a segunda lei da Termodinâmica ain-da não tinha sido formulada e a entropia era um conceito inexistente. Usando simbologia atual, a equação de Clapeyron pode ser representada pela expressão (5), onde \(T\) é a tem-peratura absoluta.


\(\frac{dp}{dT}=\frac{\Delta_{cr,l}^{g}H_{m}^{o}}{T\Delta_{cr,l}^{g}H_{m}^{o}v_m}\)            (5)


Na expressão (5), \(v_m\) é o volume molar, tendo já sido anteriormente definidas as outras grandezas e símbolos. Esta equação é termodinamicamente exata, mas pode ser aproximada pela equação de Clausius-Clapeyron (Eq. 6), considerando simplesmente que o volume molar do gás (suposto ideal) é muito maior que o volume molar da sua fase condensada.


\(R\frac{d \ln p(T)}{dT}=\frac{\Delta_{cr,l}^{g}H_{m}^{o}}{T^2}\)            (6)


A história do desenvolvimento desta equação, desde o ponto de partida (Eq. 5), é do ponto de vista da evolução da Termodinâmica, muito interessante, estando os principais avanços ligados ao aperfeiçoamento da equação dos gases ideais.

A partir de conceitos relacionados com os ciclos de Carnot e com o artigo de Clapeyron[13], Clausius[14] propôs a equação (7) como aplicação da lei de Mariotte-Gay-Lussac.


\(pv = R[a + (t/ºC)]\)            (7)


Utilizando valores experimentais determinados por Regnault, Clausius concluiu que o melhor valor para a constante \(a\) era 273 ºC, vaticinando que a precisão do valor desta constante evoluiria à medida que a qualidade de resultados experimentais fosse melhorando.

De referir que já em 1848, William Thomson (1824-1907), mais tarde homenageado com o título de Lorde Kelvin, tinha publicado um artigo onde calculou que o zero absoluto de temperatura seria -273 ºC[15]. Mas foi apenas em 1864 que Clausius adoptou as designações “temperatura absoluta” e “gás ideal” tendo reescrito a equação (7) como


\(pv = RT\)            (8)


Note-se que os volumes utilizados na altura eram volumes específicos e não volumes molares. \(R\) só foi promovida a constante universal por August Horstmann (1842-1929), ex-aluno de Clausius, que em 1873 utilizou o volume molar, que designou por \(u\), na equação (9), em vez do volume específico \(v\)[16].


\(pu = RT\)            (9)


A equação de Clausius-Clapeyron (6) pode ser facilmente integrada se o valor da entalpia de transição de fase for considerado independente da temperatura a que ocorre o equilíbrio, originando a equação (10), onde \(B\) é uma constante.


\(R \ln\frac{p(T)}{p^o}=B-\frac{\Delta_{cr,l}^{g}H_{m}^{o}}{T/K}\)            (10)


Neste caso, a representação gráfica de \(\ln[p(T)/ p^o] = \tt{f}(\tt 1/\it T)\) será linear, permitindo calcular o valor da entalpia de transição de fase a partir do declive. No entanto, \(\Delta_{cr,l}^{g}H_{m}^{o}\) dificilmente pode ser considerada constante para intervalos de temperatura superiores a cerca de 10 ºC. Este intervalo será tanto menor quanto maior for o valor absoluto de \(\Delta_{cr,l}^{g}C_{m}^{o}\), que representa a diferença (sempre negativa) da capacidade calorífica isobárica entre as fases gasosa e condensada. Em rigor, o valor de \(\Delta_{cr,l}^{g}H_{m}^{o}\) diminui com o aumento de temperatura até se anular quando a densidade do líquido e do vapor se igualarem, o que acontece à temperatura crítica.


As equações não-lineares – Antoine e Clarke & Glew

Várias equações (não-lineares) têm sido propostas para representar a variação da pressão de vapor com a temperatura. Referem-se a seguir apenas duas, de aplicação simples. A primeira foi proposta por Louis C. Antoine em 1888 e tem resistido ao tempo e às modas, continuando a ser a equação de pressão de vapor mais utilizada, especialmente para líquidos. A outra, menos conhecida e muito mais recente, é a equação de Clarke & Glew.

Antoine (1825-1898) interessou-se pelo estudo da relação entre pressão de vapor e temperatura questionando-se sobre a possibilidade da temperatura ser relativa a um zero especial para cada substância. Esse zero corresponderia à temperatura à qual a pressão de vapor do líquido era (aproximadamente) zero. Assim, em alternativa à linearidade da equação de Clausius-Clapeyron, Antoine propôs, em 1888[17], a curva representada pela equação (11), conhecida como equação de Antoine, onde a constante \(C\) em vez de ser \(273,15 K\) (o que sucede implicitamente na equação de Clausius-Clapeyron), é geralmente inferior a esse valor.


\(\log \frac{p(T)}{p^o}=A-\frac{B}{(t/^oC)+C}\)            (11)


A não associação direta dos parâmetros da equação (11) a propriedades termodinâmicas de transição de fase tem motivado que vários autores prefiram utilizar a equação de Clarke & Glew[18]. Esta equação foi proposta em 1966 visando a sua aplicação ao estudo de equilíbrios químicos, nomeadamente ao estudo da ionização do ácido cianoacético. Aqueles autores realçaram as vantagens da utilização de parâmetros termodinâmicos que fundamentam a equação, relativamente aos parâmetros empíricos que integram outras equações. A partir da década de setenta do século passado, C.G. de Kruif (1943-2016) e colaboradores do Grupo de Termodinâmica da Universidade de Utrecht adaptaram a equação de Clarke & Glew aos equilíbrios de sublimação ou de vaporização, sob a forma da equação (12), tendo determinado através dela propriedades termodinâmicas de transição de fase de vários compostos orgânicos[19], [20].


\(R \ln \frac{p}{p^0}=-\frac{\Delta_{cr,l}^{g}G_{m}^{o}(\theta)}{\theta}+\Delta_{cr,l}^{g}H_{m}^{o}(\theta) \left(\frac{1}{\theta}-\frac{1}{T}\right)+\Delta_{cr,l}^{g}C_{p,m}^{o}(\theta)\left[\left(\frac{\theta}{T}\right) -1+\ln\left(\frac{T}{\theta}\right)\right]+\)

\(+\left(\frac{\theta}{2}\right)(d\Delta_{cr,l}^{g}C_{p,m}^{o}/dT)_\theta\left[\left (\frac{T}{\theta}\right)-\left(\frac{\theta}{T}\right)-\ln\left(\frac{T}{\theta}\right)\right]+\)...            (12)


Nesta equação \(\theta\) e \(po\) são, respetivamente, uma temperatura e uma pressão de referência, \(\Delta_{cr,l}^{g}C_{p,m}^{o}\) representa a diferença da capacidade calorífica isobárica entre as fases gasosa e condensada e os outros símbolos representam propriedades termodinâmicas já definidas anteriormente. Para resultados de pressões de vapor determinados com boa precisão dentro de intervalos de temperatura superiores a 50 ºC, é possível a partir do ajuste da equação (12) aos valores (\(p\),\(T\)) obter valores fiáveis não só de \(\Delta_{cr,l}^{g}G_{m}^{o}\) e de \(\Delta_{cr,l}^{g}H_{m}^{o}\) como também de \(\Delta_{cr,l}^{g}C_{p,m}^{o}\) e, para intervalos de temperatura mais extensos, o valor da sua variação com a temperatura (\(d\Delta_{cr,l}^{g}C_{p,m}^{o}/dT\))[21].

Na FIGURA 3 apresenta-se um diagrama de fases do composto p-hidroxibenzaldeído, onde as linhas curvas resultam do ajuste da equação de Clarke & Glew às pressões de vapor experimentais, incluindo as pressões de vapor do líquido sobre-arrefecido - esta é uma fase metaestável, que acontece frequentemente quando um líquido bem desgasificado é arrefecido, permanecendo líquido até uma temperatura que pode ser inferior, até cerca de 30 ºC, à temperatura do ponto triplo.


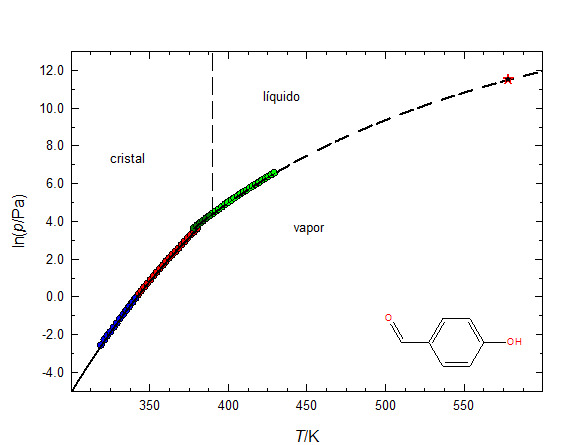
FIGURA 3. Diagrama de fases do composto p-hidroxibenzaldeído: Verde claro, pressões de vapor da fase líquida (método estático); verde escuro, pressões de vapor do líquido sobrearrefecido (método estático); vermelho, pressões de vapor da fase cristalina (método estático); azul, pressões de vapor da fase cristalina (método de efusão de Knudsen); Estrela, temperatura de ebulição normal (extrapolação da curva do equilíbrio líquido-vapor para p = 1 atm). Coordenadas do ponto triplo determinadas pela intercepção da curva \(cr-g\) e da curva \(liq-g: T = 389.8 K; p = 79.3 Pa\). Figura adaptada da ref.21


Aplicações do conhecimento de pressões de vapor

Desde as determinações de Dalton, muito se alargou o espetro da aplicabilidade de valores de pressão de vapor. Além de diversas aplicações industriais, na linha da frente aparece a determinação de entalpias de sublimação e de vaporização a partir da medição experimental de pressões de vapor a diferentes temperaturas, em detrimento de determinações calorimétricas que só raramente são ainda utilizadas.

O conhecimento da volatilidade de substâncias poluentes é também de crucial importância no âmbito das ciências do ambiente. Por exemplo, os compostos mais voláteis tendem a escapar com facilidade (sob a forma gasosa) para a atmosfera e a condensar em zonas mais frias regressando ao solo com as chuvas ou quedas de neve. A disponibilidade de valores de pressões de vapor é fundamental para a avaliação da mobilidade ambiental desses compostos, tendo em vista a previsão do seu destino e o controle de riscos químicos, quer ambientais, quer ligados à higiene ocupacional. Combinada com valores de solubilidade, a pressão de vapor permite calcular energias de Gibbs de solvatação, \(\Delta_{solv}G_m^o\) (cr,l) também utilizadas em estudos ambientais[22] e necessárias à determinação de energias de Gibbs de associação entre novos fármacos e os seus recetores, um dos objetivos da moderna bioinformática.

A pressão de vapor possibilita ainda (via energias de Gibbs de sublimação ou vaporização) a determinação da energia de Gibbs de formação em fase condensada, a partir de valores calculados em fase gasosa. Esta propriedade, \(\Delta_{\tt f}G_m^o\) (cr,l), permite avaliar a estabilidade termodinâmica de compostos cristalinos ou líquidos e a determinação de constantes de equilíbrio de reações em que eles intervenham como reagentes ou produtos[23].



AGRADECIMENTOS

Agradeço à Doutora Ana Rita Almeida a ajuda na revisão do texto.


[editar] Referências

  1. ↑ MONTE, M. J. S. et al., New static apparatus and vapor pressure of reference materials: naphthalene, benzoic acid, benzophenone and ferrocene. J. Chem. Eng. Data 51. 757-766, 2006.
  2. ↑ RIBEIRO DA SILVA, M. A. V. et al., The design, construction and testing of a new Knudsen effusion apparatus. J. Chem. Thermodyn. 38. 778-787, 2006.
  3. ↑ VEREVKIN, S. P. & EMEL´YANENKO, V. N., Transpiration method: Vapor pressures and enthalpies of vaporization of some low-boiling esters. Fluid. Phase Equilib. 266. 64–75, 2008.
  4. ↑ WEST, J. B., Joseph Black, carbon dioxide, latent heat, and the beginnings of the discovery of the respiratory gases. Am. J. Physiol. Lung Cell. Mol. Physiol. 306. L1057–L1063, 2014.
  5. ↑ DALTON, J., A New System of Chemical Philosophy. Manchester: S. Russell for R. Bickerstaff; Russell & Allen for R. Bickerstaff; Executives of S. Russell for G. Wilson, 1808-1810-1827.
  6. ↑ DALTON, J., F.R.S. (1766-1844) and the Atomic Theory-A Lecture to Commemorate his Bicentenary.
  7. ↑ WISNIAK, J., Historical Development of the Vapor Pressure Equation from Dalton to Antoine. J. Phase Equilib. 22. 622-630, 2001.
  8. ↑ WISNIAK, J., Historical Development of the Vapor Pressure Equation from Dalton to Antoine. J. Phase Equilib. 22. 622-630, 2001.
  9. ↑ BIOT, J. B., Traité de Physique Expérimentale et Mathématique, Déterville, Paris, 264-90, 1817.
  10. ↑ WISNIAK, J., Historical Development of the Vapor Pressure Equation from Dalton to Antoine. J. Phase Equilib. 22. 622-630, 2001.
  11. ↑ REGNAULT, V., Mémoires de l’Académie des Sciences. 26. 1–928, 1862.
  12. ↑ CLAPEYRON, E., J. de l’École Polytechnique 14. 153–91, 1834.
  13. ↑ CLAPEYRON, E., J. de l’École Polytechnique 14. 153–91, 1834.
  14. ↑ CLAUSIUS, R., Ann. Phys. 79, 368–97 and 500–24, 1850.
  15. ↑ THOMSON, W., On an absolute thermometric scale founded on Carnot’s theory of the motive power of heat and calculated from Regnault’s observations. Philosophical Magazine, 1848 [from Sir William Thomson, Mathematical and Physical Papers, 1. 100–106, 1882, Cambridge University Press].
  16. ↑ JENSEN, W. B., The universal gas constant R. J. Chem. Educ. 80, 731-732, 2003.
  17. ↑ ANTOINE C., Tensions des vapeurs; nouvelle relation entre les tensions et les températures. Comptes Rendus des Séances de l’Académie des Sciences 107. 681–684, 778–780, 836–837, 1888.
  18. ↑ CLARKE, E. C. W. & GLEW, D. N., Evaluation of thermodynamic functions from equilibrium constants. Trans. Faraday Soc. 62. 539-547, 1966.
  19. ↑ KRUIF, C. G. & VAN GINKEL, C. H. D. Torsion-weighing effusion vapour-pressure measurements on organic compounds. J. Chem. Thermodyn. 9. 725-730, 1977
  20. ↑ ALMEIDA, A. R. R. P. & MONTE, M. J. S., J. Chem. Eng. Data 61. 1012-1020, 2016.
  21. ↑ ALMEIDA, A. R. R. P. & MONTE, M. J. S., Vapor pressures and Gibbs energies of formation of the three hydroxybenzaldehydes. J. Chem. Eng. Data 62. 2982-2992, 2017.
  22. ↑ MONTE, M. J. S. & ALMEIDA, A. R. R. P., Estimations of the thermodynamic properties of halogenated benzenes as they relate to their environment mobility. Chemosphere 189. 590-598, 2017.
  23. ↑ OLIVEIRA, J. A. S. A. et al., Thermodynamic properties of 2,7-di-tert-butylfluorene - an experimental and computational study. J. Chem. Thermodyn. 101. 115-122, 2016.


Recursos relacionados disponíveis na Casa das Ciências:

  1. Diagramas de Fase.



Criada em 27 de Agosto de 2018
Revista em 23 de Setembro de 2018
Aceite pelo editor em 4 de Outubro de 2018

Obtida de "https://wikiciencias.casadasciencias.org/wiki/index.php?title=Pressão_de_vapor&oldid=29332"