Potencial Eléctrico
Referência : Ferreira, M., (2015) Potencial elétrico, Rev. Ciência Elem., V3(2):031
Autor: Miguel F.
Editor: Joaquim Agostinho Moreira
DOI: [http://doi.org/10.24927/rce2015.031]

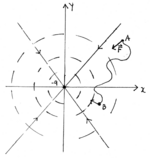
Consideremos, por simplicidade, uma carga pontual Q localizada na origem de um referencial. O Campo Eléctrico criado por esta carga num ponto 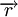 do espaço vazio é:
do espaço vazio é:
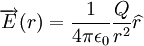
sendo 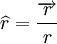 . Suponhamos que num ponto A, localizado na posição
. Suponhamos que num ponto A, localizado na posição 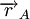 , se coloca uma outra carga pontual q. Esta carga fica sujeita a uma força de interacção eléctrica, que é descrita pela Lei de Coulomb:
, se coloca uma outra carga pontual q. Esta carga fica sujeita a uma força de interacção eléctrica, que é descrita pela Lei de Coulomb:
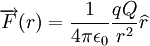
Note-se que esta força depende da posição da carga q e da distância entre as duas cargas. Agora, suponhamos que a carga q é transportada para um ponto B, cuja posição é 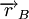 , sob a acção de uma força externa, num processo quase estático. Nestas condições, a força externa é simétrica à força eléctrica que actua na carga q. Mostra-se que o trabalho realizado pela força externa no transporte da carga q entre as posições A e B não depende do trajecto seguido pela carga q, dependendo apenas das posições inicial e final [1]. O valor do trabalho realizado pela força externa é [1]:
, sob a acção de uma força externa, num processo quase estático. Nestas condições, a força externa é simétrica à força eléctrica que actua na carga q. Mostra-se que o trabalho realizado pela força externa no transporte da carga q entre as posições A e B não depende do trajecto seguido pela carga q, dependendo apenas das posições inicial e final [1]. O valor do trabalho realizado pela força externa é [1]:
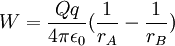
Define-se a diferença de potencial eléctrica entre os pontos A e B como sendo o trabalho realizado pela força externa por unidade de carga transportada:
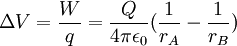
O potencial num ponto A do campo eléctrico criado pela carga pontual Q, localizada na origem do referencial, é igual ao trabalho realizado pela força externa no transporte da carga q desde o infinito até ao ponto A:
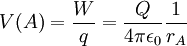
Consideremos agora um sistema formado por N cargas pontuais, de valores 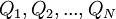 , localizadas nos pontos
, localizadas nos pontos 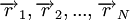 , respectivamente. Uma vez que a força eléctrica satisfaz o Princípio da Sobreposição Linear, o potencial eléctrico num dado ponto do espaço é igual à soma dos potenciais criados pelas diferentes cargas presentes:
, respectivamente. Uma vez que a força eléctrica satisfaz o Princípio da Sobreposição Linear, o potencial eléctrico num dado ponto do espaço é igual à soma dos potenciais criados pelas diferentes cargas presentes:
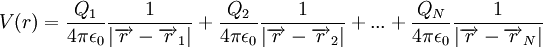
A unidade SI de potencial eléctrico é o volt (V). A diferença de potencial de 1V entre dois pontos de um campo eléctrico corresponde ao trabalho de 1 J no transporte de +1C de carga entre esses dois pontos.
Superfícies Equipotenciais
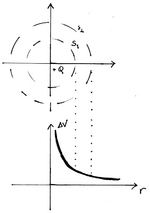
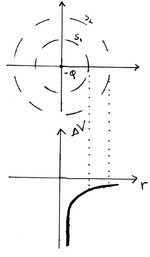
As superfícies equipotenciais são o lugar geométrico dos pontos onde o potencial eléctrico é constante. No caso de uma carga pontual, o potencial é o mesmo em todos os pontos equidistantes da carga e, por isso, as superfícies equipotenciais são superfícies esféricas concêntricas com a carga. Se a carga criadora do potencial for positiva (negativa), o potencial num dado ponto do espaço decresce (aumenta) à medida que a distância entre o ponto considerado e a carga aumenta. As figuras seguintes ilustram o que se afirmou. Note-se que as linhas de campo eléctrico (sendo radiais) são normais às superfícies equipotenciais nos pontos de intersecção, e o campo tem o sentido dos potenciais decrescentes. Esta propriedade geométrica entre linhas de campo e superfícies equipotenciais é geral. No caso em que o campo eléctrico é uniforme, as superfícies equipotenciais são planos perpendiculares à direcção do campo eléctrico.
Uma forma simples de mostrar que as linhas de campo são perpendiculares às superfícies equipotenciais nos pontos de intersecção, é considerar o trabalho realizado pela força eléctrica no transporte de uma carga q, seguindo um percurso totalmente contido numa superfície equipotencial, de um campo eléctrico uniforme. Nesta condição, mover a carga q ao longo da superfície equipotencial implica que o campo eléctrico realize trabalho nulo. Assim, recordando que o trabalho de uma força constante é:
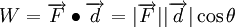 ,
,
para que o trabalho realizado seja nulo, o ângulo entre a força eléctrica e o deslocamento da carga q tem que ser 90º.Então, como a força eléctrica tem a direcção que o campo eléctrico, conclui-se que a direcção do campo eléctrico faz um ângulo de 90º com a superfície equipotencial. Uma vez que o campo eléctrico é sempre tangente às linhas de campo, as superfícies equipotencias são representadas perpendicularmente às linhas de campo.
Criada em 17 de Outubro de 2010
Revista em 27 de Maio de 2011
Aceite pelo editor em 27 de Maio de 2011