Perceptrões e redes neuronais artificiais
Referência : Aguiar, D., Aguiar, P., (2022) Perceptrões e redes neuronais artificiais, Rev. Ciência Elem., V10(1):004
Autor: Daniel Aguiar e Paulo Aguiar
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2022.004]

[editar] Resumo
Desde a segunda metade do século XX entramos num novo período da história humana: a Era da Informação. A dinâmica das nossas sociedades e o dia-a-dia de cada indivíduo, é fortemente condicionada por uma necessidade: a capacidade para obter, transmitir e processar informação. Com a revolução digital e o computador, passamos a assistir a um crescimento exponencial de dados disponíveis e, com este crescimento, surgiu também a necessidade fundamental de novas estratégias para o processamento e análise eficaz destes dados. Como em muitas outras situações de desafios científicos e tecnológicos, fomos buscar inspiração à Natureza.
Num ser vivo com sistema nervoso, as células neuronais estão constantemente a monitorizar o ambiente externo e interno do organismo, a transmitir informação sob a forma de impulsos elétricos (os chamados potenciais de ação), e a processar esta informação de forma a suportar decisões motoras. As células neuronais não são mais que o resultado de milhares de milhões de anos de evolução para um propósito muito pragmático: gestão eficaz e rápida de informação. Então, com vista ao desenvolvimento de métodos e máquinas eficazes para processar dados, porque não imitar o funcionamento de um neurónio?
Nesta linha de pensamento, uma das primeiras contribuições foi o modelo de neurónio de Warren McCulloch e Walter Pitts (1943), posteriormente refinado por Frank Rosenblatt (1958). O modelo matemático de Rosenblatt, alusivamente denominado perceptrão, procurava capturar os seguintes princípios fundamentais da dinâmica de um neurónio biológico (FIGURA 1):
a) um neurónio pode apresentar um de dois estados possíveis, ativado ou não ativado;
b) cada neurónio recebe múltiplos sinais de outros neurónios;
c) a contribuição de cada sinal de entrada é pesada pela eficácia da sua ligação (sinapse);
d) os pesos podem ser positivos ou negativos conforme a ligação é, respetivamente, excitatória ou inibitória;
e) a soma ponderada de todos os sinais de entrada produz o nível de excitabilidade total do neurónio;
f) um neurónio fica no estado ativado se a soma ponderada for superior a um valor predefinido (denominado limiar de disparo), caso contrário fica no estado não ativado.
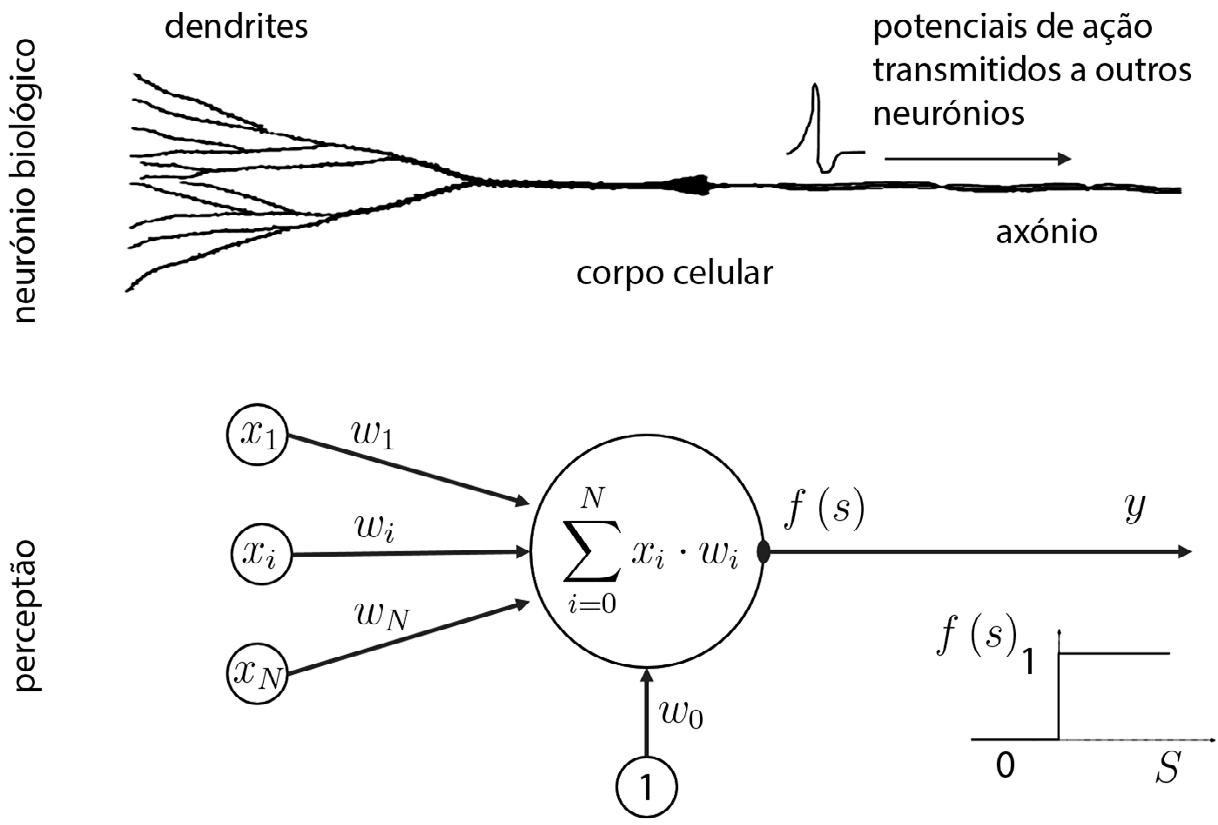
Matematicamente, o estado de ativação de um perceptrão em função dos seus sinais de entrada e dos seus pesos “sinápticos”, pode ser escrito simplesmente como:
\(y=1\) se \(\sum_{i=1}^{N}x_i \cdot w_i\geq \theta\)
\(y=0\) se \(\sum_{i=1}^{N}x_i \cdot w_i > \theta\)
onde \(y\) é o estado do perceptrão \(\left ( y\in \left \{ 0,1 \right \} \right )\), \(x_i\) é o estado de cada um dos \(N\) neurónios de entrada \(\left ( x_i\in \left \{ 0,1 \right \} \right )\), \(w_i\) é o peso (eficácia) de cada uma das ligações/sinapses de entrada \(\left ( w_i\in \mathbb{R} \right )\), e \(\theta\) é o valor do limiar de disparo. É frequente simplificar a representação do nível total da excitabilidade, fazendo \(x_0 = 1\) e \(w_0 =\theta\), conduzindo à dinâmica:
\(y=1\) se \(\sum_{i=0}^{N}x_i \cdot w_i\geq 0\)
\(y=0\) se \(\sum_{i=0}^{N}x_i \cdot w_i < 0\)
Numa versão um pouco mais recente e mais abrangente do perceptrão, o estado de cada um dos \(N\) neurónios de entrada passa a ser um valor contínuo entre 0 e 1 \(\left ( x_i\in \left [ 0,1 \right ] \right )\), descrevendo quão ativo está cada neurónio de entrada. Neste artigo usaremos esta versão.
A beleza deste modelo é que, tal como um neurónio biológico pode adaptar as suas respostas (potenciais de ação) através de modificações nas sinapses, o perceptrão também pode ser treinado através das modificações dos seus pesos \(w_i\). Mas como se ensina um perceptrão a processar informação e tomar decisões?
Para tornar a exposição mais clara, consideremos o seguinte exemplo. Numa determinada clínica, para diagnóstico de uma determinada patologia, é necessário o levantamento de múltiplos parâmetros \(x_i\). Estes parâmetros (normalizados entre 0 e 1) podem ser a pressão arterial, a temperatura corporal, a idade, entre outros. Pretende-se classificar quais os pacientes que poderão ter a patologia. A variável de saída do perceptrão (decisão binária), classifica a existência \((y = 1)\), ou não \((y = 0)\), de patologia.
O treino de um perceptrão enquadra-se dentro de uma família de métodos denominados aprendizagem supervisionada. O perceptrão é treinado com um conjunto de dados para os quais está previamente disponível uma classificação. No caso do nosso exemplo, isto significa disponibilizar um conjunto de dados de pacientes para os quais existe à partida, não só os parâmetros fisiológicos, mas também a informação clínica sobre se têm ou não a patologia.
Note-se que não é possível construir um conjunto de treino com todas as configurações possíveis: com múltiplos parâmetros descritos por variáveis contínuas, o espaço de possibilidades dos pacientes com (ou sem) a patologia é infinito. A expectativa é que, com base num conjunto de treino limitado, o modelo seja capaz de generalizar (i.e., tenha um desempenho adequado com combinações de parâmetros que não faziam parte do conjunto de treino).
Na posse de um conjunto de dados anotados (classificados), o treino de um perceptrão faz-se recorrendo ao algoritmo de Rosenblatt. Este algoritmo, também com alguma inspiração biológica, segue os seguintes passos:
- Inicialização dos pesos \(w_i\) com valores aleatórios, na primeira iteração do modelo \((t = 0)\).
- Apresentação de um exemplo do conjunto de treino, e calcular qual seria a resposta (classificação) do perceptrão.
- Com base no erro da decisão do perceptrão, adaptar os pesos (incluindo o valor do limiar de disparo) de acordo com a seguinte regra:
- Incrementar \(t\) e voltar ao ponto 2. até que se verifique uma condição de paragem (e.g. convergência dos pesos), ou se esgotem os exemplos no conjunto de treino.
\(w_i\left ( t+1 \right )=w_i\left ( t \right )+\alpha \cdot x_i\cdot \varepsilon \)
onde
\(\alpha\) é o ganho de adaptação, compreendido entre 0 e 1
\(\varepsilon \) é erro do perceptrão, \(\varepsilon =d-y\)
\(d\) é a resposta correta/desejada
Considere-se um conjunto de treino com 16 pacientes e apenas dois parâmetros fisiológicos \(x_1\) e \(x_2\) ( FIGURA 2). As variáveis que são alvo de adaptação, os pesos, têm uma representação geométrica simples: definem a equação da reta (fronteira ou reta de decisão) que separa o espaço em duas regiões com classificação distinta (\(y = 1\) ou \(y = 0\)). Em dimensões superiores \((N >2)\), o conjunto dos \(w_i\) define o hiperplano de separação. Iterações consecutivas resultam em adaptações da reta (hiperplano) em busca de minimizar os erros de classificação (FIGURA 2).
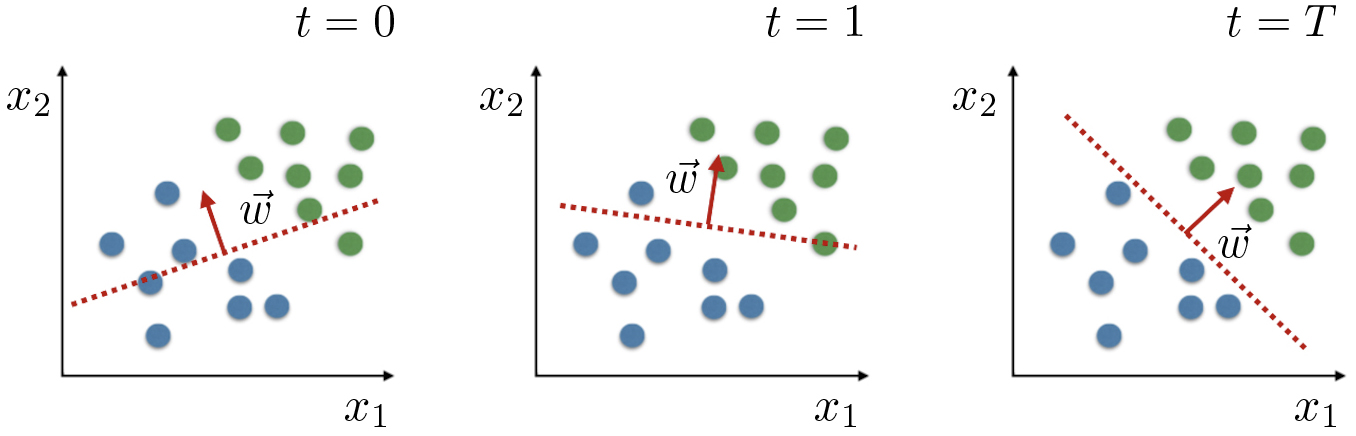
O parâmetro \(\alpha\) (ganho de adaptação), dimensiona a escala de modificação nos pesos sempre que há um erro no treino. Valores de \(\alpha\) muito reduzidos levam a uma aprendizagem muito lenta, enquanto valores de \(\alpha\) elevados podem impedir a convergência para uma situação ótima.
Após o treino com o conjunto de dados anotados, o perceptrão está pronto para ser usado em tarefas de classificação com novos dados. O desempenho do modelo está intimamente ligado à sua capacidade de generalização. No exemplo do diagnóstico de pacientes, isto significa obter classificações automáticas para a condição clínica novos pacientes.
Dos esquemas da FIGURA 2, fica claro que o perceptrão tem bons desempenhos apenas em dados linearmente separáveis. Nas condições em que as fronteiras de decisão reais são curvas (superfícies) complexas, o perceptrão terá forçosamente taxas de erros elevados. Mas se um perceptrão não é suficiente, porque não combinar múltiplos perceptrões?
Tal como os sistemas nervosos combinam múltiplos neurónios para suportar computações mais complexas, múltiplos perceptrões podem ser combinados para aumentar de forma muito significativa o desempenho em tarefas de classificação. Muitas redes neuronais artificiais usadas atualmente em tarefas de processamento complexas não são mais do que conjuntos vastos de perceptrões organizados em multicamadas: as respostas de uma camada de perceptrões serve de entrada para a próxima camada de perceptrões, até culminar num perceptrão final que disponibiliza a decisão binária (FIGURA 3).
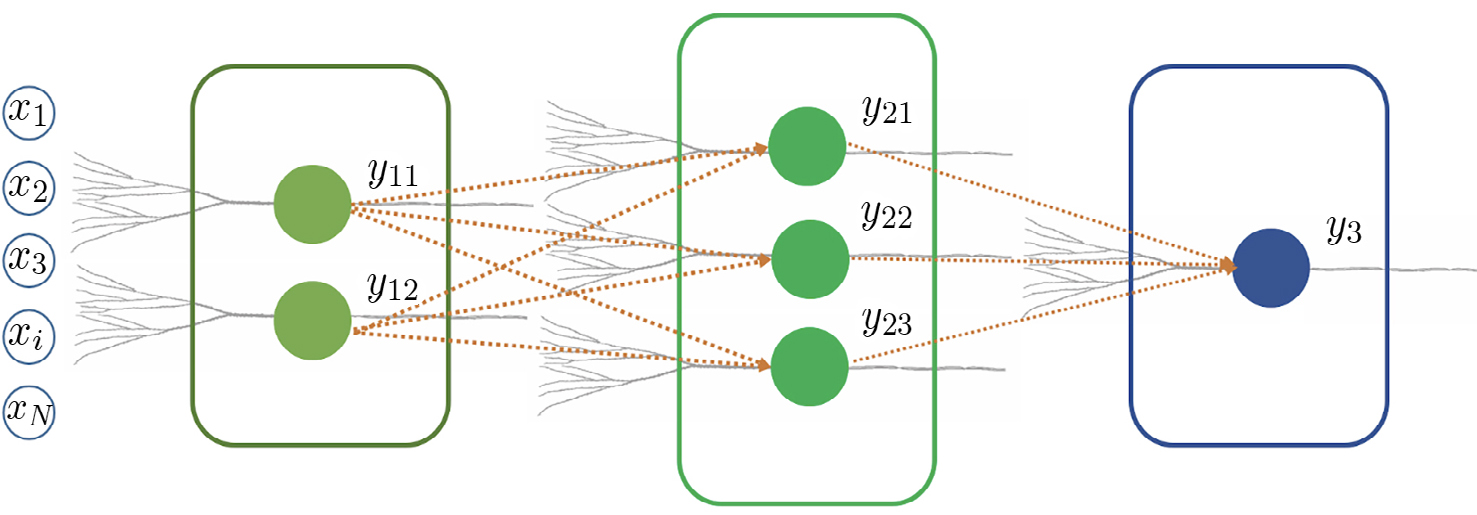
O treino de redes neuronais artificiais compostas por camadas de perceptrões é mais complexo, e não pode ser feito através do algoritmo de Rosenblatt. Na década de 80 foi desenvolvido por vários investigadores um algoritmo recursivo para este efeito, denominado método da retropropagação do erro.
As redes neuronais artificiais, como método de aprendizagem automática, dominam atualmente várias vertentes das nossas vidas. Têm um papel importante em áreas da saúde, na gestão de anúncios personalizados, no reconhecimento de voz, entre muitas outras áreas. São também parte integrante na indústria de jogos, onde podem aprender e conferir adaptação às características do jogador humano.
Desafiamos o leitor a experimentar construir o seu próprio perceptrão. Pode usar uma linguagem de programação de alto nível como o Python ou o MATLAB, como pode simplesmente usar o Microsoft Excel. Deixamos aqui um link para um perceptrão construído em Microsoft Excel: https://github.com/paulodecastroaguiar/Perceptrao_XLSX.
[editar] Referências
- MARQUES, J., Reconhecimento de Padrões - Métodos Estatísticos e Neuronais, IST Press, ISBN: 972-8469-08-X. 2005.
- MITCHELL, T. M., Machine Learning, McGraw-Hill International Editions, ISBN: 978-0071-154673. 1997.
Criada em 30 de Dezembro de 2021
Revista em 30 de Dezembro de 2021
Aceite pelo editor em 15 de Março de 2022

