Período de semi-desintegração
Referência : Lima, L.S., (2014) Período de semi-desintegração, Rev. Ciência Elem., V2(1):294
Autor: Luis Spencer Lima
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2014.294]

O período de semi-desintegração (t1/2) de uma espécie radioactiva (também designado por tempo de semi-vida, tempo de meia-vida ou período de semi-transformação) representa o intervalo de tempo que é necessário decorrer para que a sua actividade diminua para metade. Como a actividade (número de desintegrações radioactivas por unidade de tempo) é directamente proporcional ao número de núcleos atómicos radioactivos, o período de semi-desintegração é o tempo necessário para diminuir para metade o número de partículas radioactivas.
A velocidade de desintegração radioactiva é directamente proporcional ao número de núcleos presentes não desintegrados
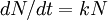
em que N representa o número de núcleos (não desintegradas) existente no instante t e λ a constante de desintegração radioactiva (ou de decaimento), o que corresponde a um processo de decaimento primeira ordem. Por integração da equação diferencial obtém-se a equação que relaciona o número de partículas não desintegradas com o tempo:

Nesta equação, N0 representa o número inicial de núcleos. A constante de desintegração (ou de decaimento) é característica de cada isótopo radioactivo (radioisótopo) e é independente da temperatura, da pressão e da substância a que o radioisótopo pertence. A partir da equação (1) pode deduzir-se a equação que permite o cálculo de t1/2. Para tal, e atendendo à definição de período de semi-desintegração, substitui-se na equação (1) N por N0/2 e t por t1/2, após rearranjo e simplificação, obtém-se

o que mostra que t1/2 é constante. Isto significa que, por cada período de semi-desintegração decorrido, o número de partículas radioactivas reduz-se para metade da anterior:
Isto significa que, ao fim de 5 períodos de semi-desintegração, restam apenas 3,125 % do número inicial de partículas. É prática corrente considerar que ao fim de 10 períodos de semi-desintegração o produto radioactivo se esgotou (a quantidade presente é cerca de mil vezes menor do que a inicial).
O período de semi-desintegração é característico de cada isótopo e pode assumir valores tão distintos como alguns milissegundos (3,4 ms é o t1/2 do meitnério-266, 266Mt) ou milhares de milhões de anos (4,468  109 anos é o t1/2 do urânio-238, 238U).
109 anos é o t1/2 do urânio-238, 238U).
Uma das aplicações mais importantes do período de semi-desintegração de um radioisótopo é na datação de objectos e é com base em t1/2 que é feita a escolha do radioisótopo mais adequado à datação do objecto em questão.
Por exemplo, se se pretende determinar a idade de uma rocha do período jurássico, ocorrido há mais de 145 milhões de anos, não se pode utilizar o método de datação com carbono-14 (14C), porque como o seu período de semi-desintegração é de 5730 anos, significa que se passaram mais de 25300 períodos de t1/2, o que implica que a quantidade de 14C é praticamente nula. Os radioisótopos mais adequados para este caso seriam, por exemplo, o 238U (t1/2 = 4,468  109 anos), o 235U (t1/2 = 7,04
109 anos), o 235U (t1/2 = 7,04  108 anos) ou o 40K (t1/2 = 1,248
108 anos) ou o 40K (t1/2 = 1,248 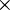 109 anos).
Para determinar a idade de um vinho, o radioisótopo mais adequado é o trítio, 3H, pois t1/2 = 12,3 anos. Quando o vinho é submetido à determinação do nível de trítio, juntamente com a água (que fornece o valor inicial de trítio), e se verifica que este apresenta apenas 30,6 % (por exemplo) da quantidade de inicial de 3H (o que significa que 69,4 % do trítio sofreu desintegração), tal significa que foi engarrafado há 21 anos.
109 anos).
Para determinar a idade de um vinho, o radioisótopo mais adequado é o trítio, 3H, pois t1/2 = 12,3 anos. Quando o vinho é submetido à determinação do nível de trítio, juntamente com a água (que fornece o valor inicial de trítio), e se verifica que este apresenta apenas 30,6 % (por exemplo) da quantidade de inicial de 3H (o que significa que 69,4 % do trítio sofreu desintegração), tal significa que foi engarrafado há 21 anos.
Criada em 16 de Dezembro de 2010
Revista em 16 de Dezembro de 2010
Aceite pelo editor em 17 de Dezembro de 2010

