Paradoxos
Referência : Tavares, J. N., (2023) Paradoxos, Rev. Ciência Elem., V11(3):035
Autora: João Nuno Tavares
Editor: João Nuno Tavares
DOI: [https://doi.org/10.24927/rce2023.035]

[editar] Resumo
Zenão de Eleia (cerca de 490/485 a.C.–430 a.C.?) foi um filósofo pré-socrático da escola eleática que nasceu em Eleia, hoje Vélia, Itália. Discípulo de Parménides de Eleia, defendeu de modo apaixonado a filosofia do mestre. O seu método consistia na elaboração de paradoxos. Deste modo, não pretendia refutar as teses que combatia mas sim mostrar os absurdos daquelas teses (e, portanto, sua falsidade). Acredita-se que Zenão tenha criado cerca de quarenta destes paradoxos, todos contra a multiplicidade, a divisibilidade e o movimento (que nada mais são que ilusões, segundo a escola eleática).
Paradoxos clássicos de Zenão de Eleia.
Os três paradoxos de Zenão listados na ”Física” de Aristóteles (Estagira, 384 a.C.—Atenas, 322 a.C.) são os seguintes:
Dicotomia.
”O que está em movimento deve chegar a meio do caminho antes de chegar ao destino.” Descrito por Aristóteles, Física VI: 9, 239b10.
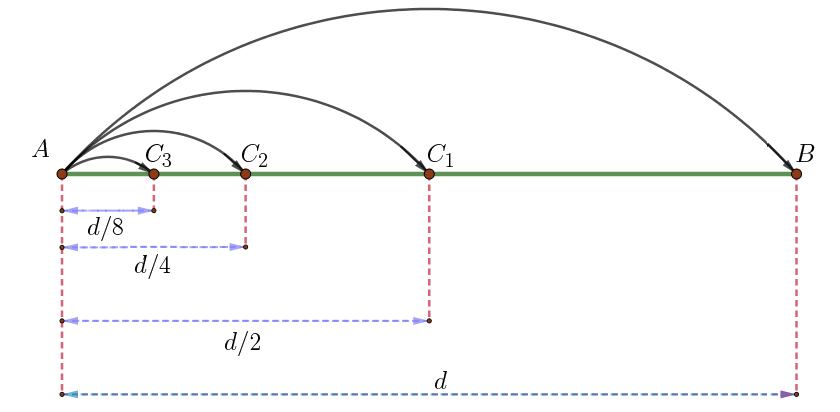
Um objeto em movimento nunca alcançará qualquer ponto dado. Mais concretamente, suponha que o leitor quer ir do ponto \(A\) ao ponto \(B\), com \(d=\overline{AB}\). Antes de chegar ao ponto \(B\), deverá chegar ao ponto \(C_1\), a meio caminho entre \(A\) e \(B\). Antes de chegar ao ponto \(C_1\), no entanto, o leitor deverá chegar ao ponto \(C_2\), a meio caminho entre \(A\) e \(C_1\), e assim sucessivamente (FIGURA 1).
Se continuarmos este processo para sempre, terminaremos com uma sequência de distâncias a percorrer do tipo
\(\left \{ \cdots,\frac{d}{2^n},\cdots,\frac{d}{8},\frac{d}{4},\frac{d}{2} \right \}\)
onde
distância de \(A\) a \(C_n=\frac{d}{2^n},n=1,2,3,\cdots\)
Mas isto é impossível, como afirma Zenão, já que há uma infinidade de etapas a cumprir antes de alcançar o objetivo de chegar a \(B\), o que é impossível num tempo finito!
Além disso, deste cenário resulta um segundo problema– não existe uma primeira distância a percorrer! De facto, qualquer possível ”primeira” distância finita, poderia ser subdividida em duas e, portanto, deixaria de ser a ”primeira” distância a percorrer. Para Zenão, isso significa que a viagem nem sequer poderia começar!
A conclusão que Zenão tira é a seguinte: percorrer uma qualquer distância finita não pode ser completada nem iniciada e, por isso, todo o movimento é uma ilusão! Conclusão que, como todos sabemos, é absurda. Onde está então o erro de Zenão? Discutiremos isto na secção seguinte.
Mas, para já, mais um dos paradoxos de Zenão, talvez o mais familiar– o paradoxo de Aquiles e a Tartaruga.
Aquiles e a Tartaruga.
”Numa corrida, o corredor mais rápido nunca pode ultrapassar o mais lento, já que o perseguidor deve primeiro alcançar o ponto de onde partiu o perseguido, e, por isso, o mais lento deve manter sempre a liderança.""
Descrito por Aristóteles, Física VI: 9, 239b15.
Imagine uma corrida entre Aquiles, um herói da guerra de Tróia, e uma Tartaruga. Como a Tartaruga é mais lenta, ela parte com uma vantagem inicial, digamos, de 10 metros.
Aparentemente, Aquiles nunca alcançará a Tartaruga! Porquê? Porque sempre que Aquiles se move a distância que o separa da Tartaruga, ela já se moveu e está, por isso, ainda à frente de Aquiles. O argumento é semelhante ao da Dicotomia. Analisaremos este paradoxo com mais detalhe na secção seguinte.
Finalmente um terceiro paradoxo, o mais intrigante, na minha opinião, que será discutido na secção 4.
A Flecha Voadora.
”É impossível uma flecha estar em movimento durante um período de tempo, porque é impossível que ela se mova em cada instante indivisível.”
Descrito por Aristóteles, Física VI: 9, 239b10.
Imagine uma flecha que se move no espaço. Em qualquer instante de tempo, sem duração temporal, a flecha não se move para onde está, nem para onde não está. Como sabemos, para ocorrer o movimento, um objeto deve mudar a sua posição. Mas em qualquer instante de tempo a flecha não muda de posição. Como o tempo é composto inteiramente de instantes, então o movimento é impossível! Note que, ao contrário do paradoxo anterior, que divide o espaço, este paradoxo divide o tempo. Além disso, este paradoxo não divide o tempo em segmentos, mas sim em pontos (instantes, sem duração).
Os paradoxos de Zenão levantam uma questão fundamental sobre o universo: será que o tempo e o espaço são contínuos, infinitamente divisíveis, como habitualmente os concebemos, ou serão discretos, havendo uma unidade mínima indivisível de espaço e, analogamente, para o tempo? Estas são questões muito atuais que têm motivado acesa controvérsia nas comunidades científicas de físicos, filósofos da ciência e matemáticos.
Uma abordagem puramente matemática.
Se aceitarmos a coerência e o rigor do chamado cálculo infinitesimal, estudado logo nos primeiros anos de qualquer curso superior de matemática, física, biologia, economia, etc., e até já no ensino secundário, a ”resolução” dos paradoxos é quase imediata.
Os processos infinitos do cálculo foram sempre um ponto problemático durante séculos, devido à falta de rigor matemático que demorou muito a construir. Muitos argumentos do cálculo eram heurísticos, como os usados nos Principia Mathematica de Isaac Newton, no século XVII, ou nos grandes avanços feitos pelo matemático Euler no século XVIII, para citar apenas dois dos mais notáveis exemplos. No entanto, no final do século XIX, as obras de Weierstrass e Cauchy acrescentaram muito rigor ao cálculo e estabeleceram uma fundamentação lógica sólida sobre os processos infinitos– limites, continuidade, formalização do cálculo diferencial, criado por Newton e Leibniz, no século XVII, etc.
Usando esta base teórica rigorosa, do ponto de vista matemático, podemos ”resolver” os dois paradoxos de Zenão (Dicotomia e Aquiles/Tartaruga) com facilidade. Vejamos como.
Dicotomia.
O paradoxo da dicotomia, pode ser resolvido com recurso à série geométrica (FIGURA 2).
\(\frac{d}{2}+\frac{d}{4}+\frac{d}{8}+\cdots=\sum_{n=1}^{\infty }\frac{d}{2^n}\)
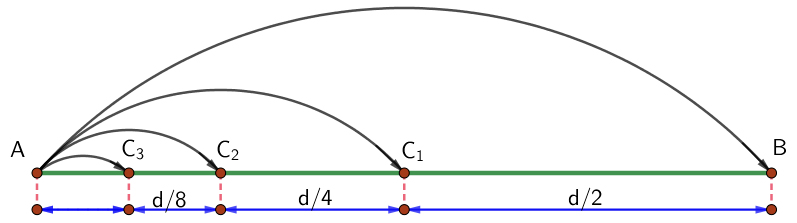
Mas será que isto prova que é possível percorrer a infinidade de distâncias
\(\left \{ \cdots,\frac{d}{2^n},\cdots,\frac{d}{8},\frac{d}{4},\frac{d}{2} \right \}\)
num tempo finito, digamos \(T\))? Mais uma vez — se aceitarmos a solução referida atrás, baseada no cálculo infinitesimal, que nos diz que a série:
\(\sum_{n=1}^{\infty }\frac{d}{2^n}=d\)
é convergente (por ser uma série geométrica de razão \(0 <\) \(r = 1/2 <\) \(1\)), então percorrer essa infinidade de distâncias seria o mesmo que percorrer a distância \(d\) num tempo finito \(T\). Portanto com velocidade (suposta constante) igual a \(v\equiv d/T\). Cada um das distâncias seria percorrida com velocidade \(v\) e o tempo que demora a percorrer a distância \(d/2^n\) seria \(t_n=\frac{d/2^n}{d/T}=T/2^n\), cada vez mais pequeno e convergindo para zero. Zenão diria que a soma destas durações finitas teria que ser infinita e que portanto, só seria possível percorrer a infinidade de distâncias num tempo infinito (uma eternidade) o que prova a impossibilidade de movimento. Mas segundo o cálculo infinitesimal \(\sum_{n=1}^{\infty }t_n=\sum_{n=1}^{\infty }T/2^n=T\) e não há contradição.
Aquiles e a Tartaruga.
Suponhamos que Aquiles \(\left ( A \right )\) corre dez vezes mais rápido do que a Tartaruga \(\left ( T \right )\), isto é, Aquiles corre 10 m/s enquanto que a Tartaruga corre apenas 1 m/s. Suponhamos ainda que a Tartaruga parte com 10m de avanço (FIGURA 3).
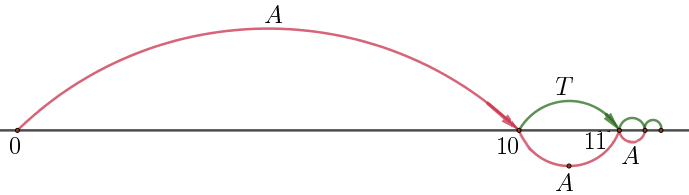
\(A\) e \(T\) iniciam a corrida no mesmo instante, digamos, \(t = 0\). Ao fim de 1 segundo, A alcança a posição de partida de \(T\), situada no ponto (de abcissa) 10 e, durante esse segundo, a Tartaruga, \(T\), avança 1 m, atingindo o ponto (de abcissa) 11. Agora \(A\) procura alcançar \(T\), avançando 1 m, para atingir o ponto 11, ao fim de um intervalo de tempo igual a 0,1 s. Mas entretanto, nesse mesmo intervalo de tempo, a Tartaruga, \(T\), avança 0.1m, atingindo o ponto 11,1.
O processo repete-se e Aquiles \(A\) nunca atingirá a Tartaruga \(T\)! Mas, mais uma vez acreditando que \(A\) e \(T\) conseguem realizar um número infinito de tarefas do tipo descrito, em tempo finito, \(A\) atinge \(T\), exatamente no ponto de abcissa:
\(\begin{matrix} 10+1+\frac{1}{10}+\frac{1}{100}+\cdots & = & 10+1\frac{1}{10}+\frac{1}{100}+cdots\\ & = & 10+\frac{1}{1-1/10}\\ & = & 10\frac{10}{9}=11,111111... \end{matrix}\) (1)
Mas isto é contra-intuitivo: como realizar um número infinito de tarefas em tempo finito? Para Zenão isto não é possível, como já vimos. Mas, se aceitarmos a consistência lógico-matemática do cálculo infinitesimal, isto só é possível se o tempo de duração das sucessivas tarefas convergir para zero. E com que ”relógio” meço essa duração ”infinitesimal”? Qualquer ”relógio” físico tem uma precisão finita, embora possa ser extremanente pequena. À escala de Planck, essa precisão será igual ao chamado Tempo de Planck \(=\tau _P=5,39121\times 10^{-44}\), o que significaria que teria que haver uma infinidade de tarefas com durações inferiores a \(\tau _P\). Mas ninguém tem dúvida– na realidade Aquiles atinge a Tartaruga!
O paradoxo da Flecha.
Imagine uma flecha voando. Em cada instante no tempo, ela estará localizada numa posição específica. Se o instante for de duração 0, então a flecha não tem tempo para se mover (mudar de posição) e fica em repouso durante esse instante. Nos instantes subsequentes, deve continuar imóvel pela mesma razão. Uma vez que o tempo total que demora o voo, consiste apenas de um conjunto discreto de instantes (de duração 0), em cada um dos quais a flecha está em repouso, Zenão conclui que a flecha está sempre em repouso e não pode estar em movimento. Essa conclusão continua válida quando o ”instante” tem a duração finita do menor ”átomo” de tempo (tempo de Planck \(\tau _P=5,39121\times 10^{-44}\)s, segundo a mecânica quântica). Suponha que a flecha realmente se move durante um tal instante. Estaria então em posições diferentes no início e no fim desse instante, o que implica que o ”instante” tem um ”início” e um ”fim”, o que por sua vez implica que contém pelo menos duas partes e, portanto, não é o ”átomo” do tempo, o que conduz a uma contradição.
A solução comum deste paradoxo é a seguinte. É falacioso concluir que do facto de que a flecha não percorre nenhuma distância, em cada instante de tempo (de duração \(0\), ou até finita, como vimos) se possa deduzir que ela está em repouso. De acordo com a visão da chamada ”teoria at-at do movimento”, o movimento não tem nada a ver com o que acontece em cada instante; tem a ver com a mudança de posição em dois instantes consecutivos. Por outras palavras, o movimento é uma característica do estar em (at) locais diferentes em (at) instantes diferentes. Daí a designação de teoria at-at.
Se um objeto tem a mesma localização nos instantes contíguos, então dizemos que está em repouso; caso contrário, está em movimento. Portanto, como a flecha em voo tem diferentes posições em diferentes instantes, está em movimento.
No entanto, ainda não sabemos como se faz a transição de uma posição para outra. Essa transição será contínua, como se supõe na mecânica clássica Newtoniana, que assume que o tempo é um contínuo de instantes (de duração \(0\)), ou será descontínua?
Em mecânica clássica (Newtoniana), o tempo e o movimento são convencionalmente entendidos como contínuos, e a velocidade instantânea é definida como a taxa instantânea de variação da posição.
\(\textrm{v}\left ( t \right )=\lim_{h\rightarrow 0,h\neq0}\frac{x\left ( t+h \right )-x\left ( t \right )}{h}\)
Por isso, velocidade instantânea é uma quantidade derivada, pois depende das posições do objeto em instantes diferentes de \(t\), passados e futuros, já que \(h\) pode ser positivo ou negativo. O estado de uma partícula, num instante \(t\), é definido pela sua posição e velocidade instantâneas no instante \(t\rightarrow \left ( x\left ( t \right ),\textrm{v}\left ( t \right ) \right )\) é tratada (usualmente) como a variável dinâmica (vetorial) da partícula e a sua velocidade como quantidade derivada, já que, como dissemos, depende das posições em instantes diferentes. Finalmente a dinâmica do movimento é determinada pela célebre 2.ª Lei de Newton:
\(\mathbf{F}=m\frac{d\textrm{v}}{dt}\),
o que conduz a uma equação diferencial ordinária de 2.ª ordem, com condições iniciais \(\left ( \textrm{x}\left ( t_o \right ),\textrm{v}\left ( t_o \right ) \right )\), cuja resolução determina o movimento (passado e futuro). A apresentação usual da mecânica clássica é, portanto, naturalmente compreendida no modo at-at.
Arntzenius num artigo intitulado ”Are there really instantaneous velocities?”, faz um resumo do estado do debate, à data, sobre a existência de velocidades instantâneas.
O movimento é um dos assuntos que sistematicamente suscita controvérsia e é objeto de profunda investigação por parte de filósofos, físicos e matemáticos. É um facto experimental que os objetos podem mover-se, e objetos macroscópicos parecem mover-se continuamente. No entanto, como os objetos se movem na realidade ainda é um grande enigma. Não podemos simplesmente considerar a aparência do movimento contínuo como a imagem real do movimento. Além disso, o debate sobre a interpretação da mecânica quântica, que é considerada a teoria mais fundamental da natureza, torna o enigma do movimento ainda mais complexo, como vamos descrever já de seguida.
O paradoxo quântico de Zenão.
O paradoxo quântico de Zenão é um conceito fascinante da mecânica quântica que trata do comportamento contra-intuitivo dos sistemas quânticos sob observação contínua. Em mecânica quântica, se observarmos um sistema continuamente para ver quando se move para um novo estado, ele simplesmente não se moverá para esse estado! Fica como a seta de Zenão! Por outras palavras, ao que parece, medições frequentes impedem o sistema de evoluir.
De acordo com a interpretação mais usual da mecânica quântica (da chamada Escola de Copenhaga, desenvolvida essencialmente por Niels Bohr e Werner Heisenberg), quando um sistema quântico é medido repetidamente, o seu estado está a ser continuamente colapsado de volta ao estado original. Aparentemente, pelo menos, conseguimos ”congelar” o sistema nesse estado, e daí a percepção de que ele não evolui. Na realidade, o sistema pode evoluir, mas as medições projetam-no de volta ao estado medido a cada instante, tornando-o aparentemente estático.
A resolução desse paradoxo reside na compreensão do processo de medição em mecânica quântica. Cada medição envolve uma interação entre o sistema a ser medido e o aparato de medição. Essa interação pode fazer com que o sistema colapse num estado definido, como descrito pelo famoso ”colapso da função de onda” (segundo a Escola de Copenhaga, como já dissemos). Para sermos mais concretos, consideremos um átomo com dois estados– o estado fundamental (thin ground state), \(\left | 0 \right \rangle\), e um estado excitado \(\left | 1 \right \rangle\). O seu estado, \(\psi\), será uma sobreposição quântica do tipo:
\(\left | \psi \right \rangle=\alpha\left | 0 \right \rangle+\beta\left | 1 \right \rangle,\; \; \; \; \; \; \alpha,\beta\in \mathbb{C}:\left | \alpha \right |^2+\left | \beta \right |^2=1\)
A interpretação física da sobreposição \(\left | \psi \right \rangle=\alpha\left | 0 \right \rangle+\beta\left | 1 \right \rangle\) é a seguinte — o estado \(\left | \psi \right \rangle\) coexiste simultaneamente em dois estados: \(\left | 0 \right \rangle\) e \(\left | 1 \right \rangle\), bem como em qualquer sobreposição destes. O estado \(\left | \psi \right \rangle=\alpha\left | 0 \right \rangle+\beta\left | 1 \right \rangle\), ”armazena” uma grande quantidade de informação nos seus coeficientes \(\alpha\) e \(\beta\). No entanto, esta informação ”vive” no nível quântico. Para extrair ”informação clássica” da informação quântica, temos que medir \(\left | \psi \right \rangle\).
A mecânica quântica (segundo a Escola de Copenhaga, como já dissemos), diz-nos que o processo de medição escolhe entre alternativas, que deixam de fazer parte da descrição após essa escolha. Essa escolha produz um ”colapso” não determinístico de \(\left | \psi \right \rangle\) no estado \(\left | 0 \right \rangle\) ou no estado \(\left | 1 \right \rangle\). Grosso modo, podemos dizer que, por medição de \(\left | \psi \right \rangle\), se obtém \(\left | 0 \right \rangle\), com probabilidade \(\left | \alpha \right |^2\), ou \(\left | 1 \right \rangle\), com probabilidade \(\left | \beta \right |^2\).
Regressemos ao nosso átomo com dois estados. A absorção de um fotão de energia apropriada faz com que o átomo salte de \(\left | 0 \right \rangle\) para \(\left | 1 \right \rangle\) (FIGURA 4).
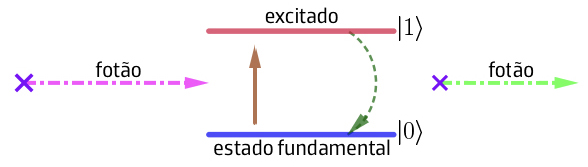
Quando o sistema é submetido a medições repetidas, a probabilidade de encontrá-lo num estado específico aumenta. É aí que o paradoxo surge.
É possível mostrar que a probabilidade de encontrar o átomo no nível de energia \(\left | 0 \right \rangle\), que é onde ele começa no tempo \(t = 0\), é dada por:
\(P_0\left ( t \right )=\cos^2\left ( \Omega t/2 \right )\)
enquanto que a probabilidade de o encontrar no nível de energia \(\left | 1 \right \rangle\) é dada por:
\(P_1\left ( t \right )=\sin^2\left ( \Omega t/2 \right )\)
ambas representadas na FIGURA 5. \(\Omega\) é a chamada frequência de Rabi, e depende da força da interação entre o fotão e o átomo. Para cada \(t\), tem-se \(P_0\left ( t \right )+P_1\left ( t \right )=1\), com teria que ser.
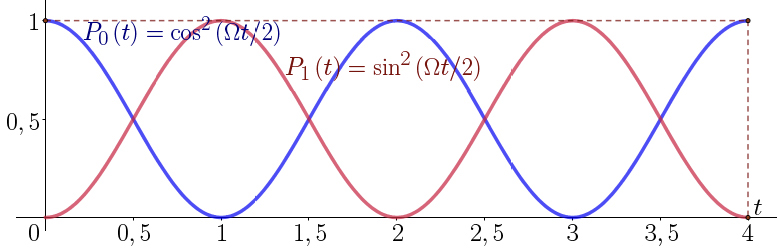
Iniciamos o átomo no estado fundamental \(\left | 0 \right \rangle\), e, depois de certo intervalo de tempo, determinamos o estado do átomo. A probabilidade \(P_0\left ( t \right )\) de que o atomo permaneça no estado \(\left | 0 \right \rangle\) é quase 1, se observarmos o átomo logo após \(t = 0\). Depois \(P_0\left ( t \right )\) decresce até chegar a \(0\) no tempo \(t = T = \pi/\Omega= 1\) s, se tomarmos \(\Omega=\pi\)/ s (FIGURA 5, curva azul). Enquanto isso acontece, a probabilidade \(P_1\left ( t \right )\) de o átomo estar no nível \(\left | 1 \right \rangle\) cresceu até 1 (FIGURA 5, curva vermelha).
Suponhamos que medimos o estado de energia do átomo no instante \(t = T/2 =\) 0,5 s. A probabilidade de o encontrar no nível \(\left | 0 \right \rangle\) é
\(P_0\left ( T \right )\cos^2\left ( \Omega T/4 \right )=\cos^2\left ( \pi/4 \right )=\) 0,5
Suponhamos que descobrimos que ele permaneceu no nível \(\left | 0 \right \rangle\); medimo-lo novamente após o mesmo intervalo de tempo. A probabilidade de que ainda esteja no estado \(\left | 0 \right \rangle\) após essas duas medições, notada por \(P\left ( 2 \right )\), é a probabilidade de que esteja no estado \(\left | 0 \right \rangle\) após a primeira medição, vezes a mesma probabilidade novamente, isto é
\(P\left ( 2 \right )\left ( \cos^2\left ( \pi/4 \right ) \right )^2=\cos^4\left ( \pi/4 \right )=\) 0,25
Suponhamos agora que fazemos quatro dessas medições, cada uma no intervalo menor \(T/4\). Então, a probabilidade do átomo permanecer ainda no estado fundamental, \(\left | 0 \right \rangle\), é igual a:
\(P\left ( 4 \right )\left ( \cos^2\left ( \Omega T/8 \right ) \right )^2=\cos^8\left ( \pi/8 \right )=\) 0,53
Desta forma, medimos com cada vez mais frequência o sistema e a probabilidade de o encontrar ainda no estado fundamental, \(\left | 0 \right \rangle\). Se o fizermos em intervalos de tempo cada vez mais curtos \(T/n\), onde \(n\geq 4\), encontramos que:
\(P\left ( n \right )=\cos^{2n}\left ( \pi/2n \right )\)
Esta probabilidade está representada na FIGURA 6. Vemos que quando o número \(n\) de medições aumenta, com o tempo entre elas cada vez mais curto, a probabilidade do átomo permanecer no estado fundamental converge para 1.
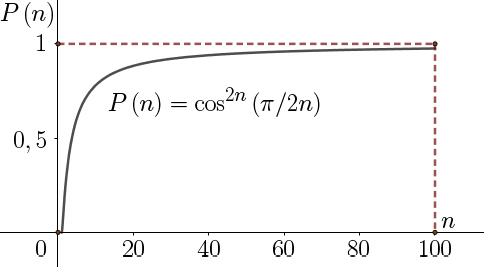
Ou seja, o átomo nunca vai para o estado excitado \(\left | 1 \right \rangle\) e portanto não se move — fica congelado no estado fundamental \(\left | 0 \right \rangle\). Este é o efeito quântico de Zenão.
É importante realçar que o paradoxo quântico de Zenão não é uma violação das leis da mecânica quântica, mas sim um reflexo do próprio processo de medição quântica. Na verdade, esse paradoxo desafia a nossa intuição clássica e revela que o mundo quântico é intrinsecamente diferente do mundo macroscópico que experimentamos no dia a dia. O paradoxo surge quando perguntamos o que acontece a um sistema quântico se fizermos medições frequentes para verificar a sua posição ou qualquer outro atributo. Se medirmos o estado do sistema em intervalos muito curtos, a sobreposição de estados não terá tempo suficiente para evoluir de uma forma para outra — o sistema parece ”congelar” no seu estado atual e nunca evolui para um estado diferente.
Esse paradoxo tem implicações práticas na computação quântica e no controle quântico, onde a medição contínua pode ser utilizada para estabilizar sistemas quânticos e proteger informações quânticas frágeis.
[editar] Referências
- HAMZA, E., Paradoxes. Guiding Forces in Mathematical Exploration, Curious Math Publications, ISBN-10: 1735715611. 2020.
- ARNTZENIUS, F., Are There Really Instantaneous Velocities?, The Monist, vol. 83, no. 2, pp. 187-208. 2000.
- MULLIN, W. J., Quantum Weirdness, Oxford University Press, ISBN-10: 0198854366. 2020.
- GREENSTEIN, G. & ZAJONC, A. G., The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Jones and Barlett Publishers. 1997.
- WAYNE, M. et al., Quantum Zeno effect, Physical Review A., Volume 41, Number 5. 1990.
- SMITH, S. R., Are instantaneous velocities real and really instantaneous? an argument for the affirmative, Studies in History and Philosophy of Modern Physics, 34, 261280. 2003.
- ROHRLICH, Y. A. D., Quantum Paradoxes Quantum Theory for the Perplexed, WILEY-VCH Verlag GmbH & Co. KGaA, ISBN-10: 3-527- 40391-4. 2005.
Criada em 27 de Junho de 2023
Revista em 27 de Julho de 2023
Aceite pelo editor em 13 de Outubro de 2023

