Pêndulo Simples
Referência : Lage, E., (2018) Pêndulo simples, Rev. Ciência Elem., V6(3):054
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2018.054]

O pêndulo simples (FIGURA 1) é um dos instrumentos mais antigos para medir o ritmo do tempo.
Trata-se de um pequeno corpo (massa m) preso na extremidade de um fio, o qual tem a outra extremidade
fixa num
ponto. Fazendo-o oscilar num campo gravítico uniforme, o pêndulo apresenta oscilações isócronas, i.e. que se
realizam com o mesmo período, para pequenas amplitudes, o que o torna num precioso relógio que também pode ser
usado para medir indiretamente a longitude, fundamental para a navegação até ao sec. XVIII, ou para medir a
intensidade do campo gravítico local, com importantes aplicações em Geofísica. Diz-se que o isocronismo do
pêndulo foi descoberto por Galileu quando, numa missa, observou a oscilação de um candelabro suspenso do teto da
igreja, tendo medido o período através da contagem dos seus batimentos cardíacos. Seja como for, Galileu viria a
usar o pêndulo nas suas experiências com o plano inclinado.

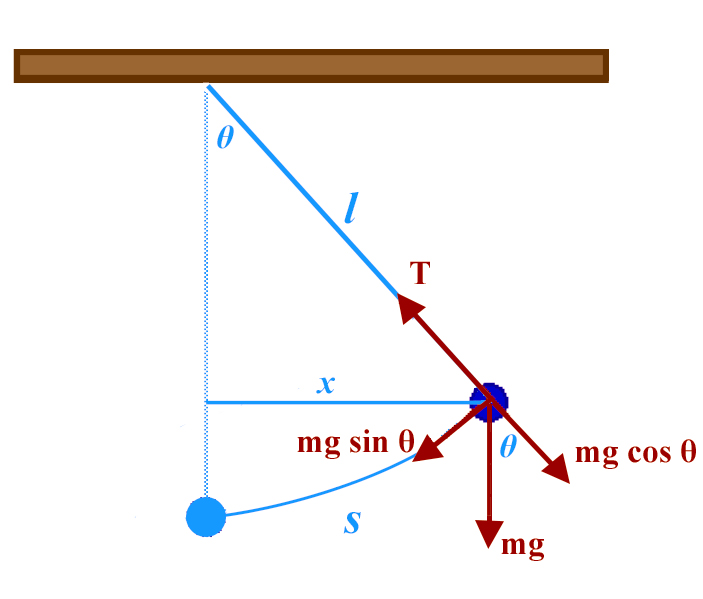
Analisaremos aqui o mais simples dos movimentos do pêndulo, sua oscilação num plano vertical e para pequenas amplitudes, admitindo que o fio é inextensível e sem peso (pêndulo ideal) e que a pequena massa é pontual. A FIGURA 2 ilustra a parametrização do pêndulo, de comprimento \(l\), e as forças em jogo. A posição do pêndulo é inteiramente determinada pelo ângulo \(\theta\) que o fio faz com a vertical - por isso se refere que este sistema tem um único grau de liberdade. Há duas forças que atuam na pequena massa suspensa: a tensão do fio (\(T\)), dirigida na direção do fio e sentido apontando para o ponto de suspensão; e o peso (\(mg\)), vertical. A força que puxa a massa para a sua posição de equilíbrio é, apenas, a componente do peso tangente ao arco de circunferência que a massa executa na sua oscilação. Simples geometria mostra que esta força vale \(mgsen\theta\), como se mostra na figura. Para pequenas oscilações, é \(\theta << 1\) (ângulo expresso em radianos), pelo que \(sen(\theta) ≅ \theta =\frac{s}{l}\), onde \(s\) é o arco da circunferência (medido a partir da posição de equilíbrio, i.e., da vertical). Nestas circunstâncias, o arco confunde-se com a corda (\(x\)), pelo que a força restauradora se escreve \(-mg\), com o sinal a indicar que a força puxa para a origem quer quando \(x > 0\), quer quando \(x < 0\). Assim, a equação de movimento é a de um simples oscilador harmónico:
\(m\frac{d^2x}{dt^2}=-mg\frac{x}{l}\)
Então, a frequência natural deste movimento é \(\omega_0\sqrt{\frac{g}{l}}\) e, portanto, o período da oscilação é \(2\pi \sqrt{\frac{l}{g}}\), independente da amplitude do movimento (apenas para pequenas amplitudes).
Mas o pêndulo também pode ser posto a rodar em torno da vertical, um movimento que tantas vezes observamos quando, distraidamente, fazemos girar as chaves de casa ou do automóvel suspensas por uma fina corrente. Estes dois tipos de movimento - oscilação e rotação - correspondem aos dois graus de liberdade que o pêndulo apresenta, por exemplo, o mesmo ângulo \(\theta\) que o fio faz com a vertical, e o ângulo \(\phi\) que o plano do pêndulo, definido pelo fio e pela vertical passando pelo ponto de sustentação, faz com um outro plano vertical fixo. Estes dois movimentos só em situações simples se apresentam separados - no caso geral, eles interferem mutuamente originando uma riqueza de comportamentos que nos surpreende. O estudo completo do pêndulo simples é feito mais detalhadamente num outro artigo.
[editar] Referências
- GOLDSTEIN, H. et al., Classical Mechanics, Addison Wesley 3ª edição, 2001.
- FEYNMAN, R.P. et al., The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley ,Vol. 1, section 12-5, 2006. ISBN 0-8053-9049-9
- LANDAU, L.D. e LIFSHITZ, E.M., Mechanics. Course of Theoretical Physics. Vol. 1 (3rd ed.). Butterworth-Heinenan, pp. 128-130, 1976.
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 24 de Abril de 2018
Revista em 22 de Setembro de 2018
Aceite pelo editor em 4 de Outubro de 2018

