Operações com acontecimentos
Referência : Martins, E.G.M., (2015) Operações com acontecimentos, Rev. Ciência Elem., V3(2):127
Autores: Maria Eugénia Graça Martins
Editor: José Francisco Rodrigues
DOI: [http://doi.org/10.24927/rce2015.127]

Existindo um paralelismo entre conjuntos e acontecimentos às operações definidas entre conjuntos correspondem operações definidas entre acontecimentos. No entanto, há uma terminologia própria para acontecimentos, que se exemplifica a seguir recorrendo aos diagramas de Venn. Considere-se um espaço de resultados S e os acontecimentos A, B, C, ..., associados a S.
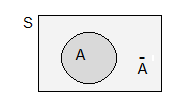
- 1. Acontecimento complementar ou contrário do acontecimento A
O acontecimento complementar ou contrário do acontecimento A, representa-se por \({\bf{\bar A}}\) ou \( {\bf{A^C}}\) e é o acontecimento constituído por todos os resultados de S, que não estão em A.
- 2. Acontecimento A implica acontecimento B
A realização do acontecimento A implica a realização do acontecimento B, quando todo o resultado de A é um resultado de B; indica-se este facto escrevendo \({\bf{A}} \subseteq {\bf{B}}\).
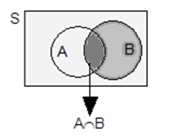
- 3. Acontecimento Interseção
Interseção dos acontecimentos A e B, \({\bf{A}} \cap {\bf{B}}\), ou (\({\bf{A}} \ {\bf{e}} \ {\bf{B}}\)), é o acontecimento que se realiza se e só se A e B se realizam simultaneamente. O acontecimento \({\bf{A}} \cap {\bf{B}}\) é constituído pelos resultados comuns a A e a B.
O acontecimento impossível é o que resulta da interseção de dois acontecimentos disjuntos. Analogamente ao que se passa na teoria dos conjuntos, representa-se por \(\emptyset\) ,símbolo do conjunto vazio, mas que aqui se lê acontecimento impossível e não acontecimento vazio.
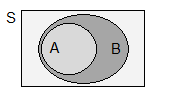
- 4. Acontecimento União
União dos acontecimentos A e B, \({\bf{A}} \cup {\bf{B}}\) , ou (\({\bf{A}} \ {\bf{ou}} \ {\bf{B}}\)) é o acontecimento que se realiza se e só se A ou B se realizam. O acontecimento \({\bf{A}} \cup {\bf{B}}\) é constituído pelos resultados que pertencem a pelo menos um dos acontecimentos A ou B.
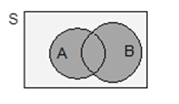
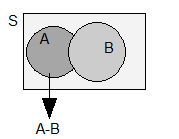
- 5. Acontecimento Diferença
Acontecimento diferença entre A e B, \({\bf{A}} \ {\bf{-}} \ {\bf{B}}\), é o acontecimento que se realiza se e só se A se realiza, sem que B se realize. O acontecimento \({\bf{A}} \ {\bf{-}} \ {\bf{B}}\) é constituído pelos resultados que pertencem a A e não pertencem a B.
Ver
Referências
GRAÇA MARTINS, M. E., MONTEIRO, C., VIANA, P. V., TURKMAN, M. A. A. (1999) – Probabilidades e Combinatória. Ministério da Educação, Departamento do Ensino Superior. ISBN: 972-8417-33-0. Depósito Legal 143440/99.
Criada em 14 de Maio de 2012
Revista em 04 de Janeiro de 2013
Aceite pelo editor em 04 de Janeiro de 2013