Lei de Hess
Referência : Lima, L.S., (2015) Lei de Hess, Rev. Ciência Elem., V3(1):094
Autor: Luis Spencer Lima
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2015.094]
A lei de Hess surge na Termoquímica como uma consequência do princípio da conservação da energia e do facto de uma função de estado depender apenas dos estados inicial e final e não do caminho percorrido entre ambos. Refere-se à aditividade de valores de variação de entalpia padrão de reacções químicas ( rHº) que podem ser utilizadas na estimativa da variação de entalpia de uma reacção difícil (ou mesmo impossível) de medir experimentalmente.
rHº) que podem ser utilizadas na estimativa da variação de entalpia de uma reacção difícil (ou mesmo impossível) de medir experimentalmente.
Por exemplo, se se pretender saber o valor de  rHº da reacção A
rHº da reacção A 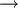 B mas não for possível efectuar uma medição directa, podem ser utilizadas outras reacções para as quais se conhecem ou se podem medir os valores de
B mas não for possível efectuar uma medição directa, podem ser utilizadas outras reacções para as quais se conhecem ou se podem medir os valores de  rHº (por exemplo, as reacções A
rHº (por exemplo, as reacções A 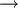 C e C
C e C 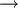 B), desde que, quando “somadas” as equações químicas intermediárias originem a equação química cujo valor de
B), desde que, quando “somadas” as equações químicas intermediárias originem a equação química cujo valor de 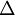 rHº interessa obter:
rHº interessa obter:
A 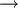 C C |
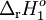 |
|
"+" |
C 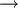 B B |
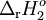 |
A 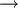 B B |
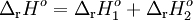 |
|
Foi em 1840 que Germain Henri Hess (1802-1850), médico e químico nascido na Suíça e naturalizado russo, publicou o seu artigo mais conhecido[1], onde descreve os princípios que constituem a base daquela que é hoje conhecida como Lei de Hess, assim denominada em sua homenagem. Para a correcta aplicação/utilização da Lei de Hess, tem de se ter em consideração os seguintes pontos:
Os valores de variação de entalpia devem ter uma base molar e ser referentes aos mesmos valores de pressão e temperatura, normalmente à pressão que define estado padrão (po = 105 Pa) e à temperatura de referência T = 298,15 K (25,00 ºC);
Qualquer operação que afecte a equação química intermediária em questão, afecta da mesma forma o seu valor de
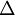 rHº. Por exemplo, se a equação química for invertida, o sinal de
rHº. Por exemplo, se a equação química for invertida, o sinal de 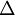 rHº é o seu simétrico; se se multiplicarem os coeficientes estequiométricos de uma equação por um número inteiro ou fraccionário, o valor de
rHº é o seu simétrico; se se multiplicarem os coeficientes estequiométricos de uma equação por um número inteiro ou fraccionário, o valor de 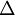 rHº também deverá ser multiplicado por esse número;
rHº também deverá ser multiplicado por esse número;3. Ao “somarem-se” as equações químicas intermediárias, devem reduzir os termos semelhantes (isto é, anular as mesmas quantidades de substâncias no mesmo estado físico comuns aos reagentes e produtos). Por exemplo, se existirem 4 moles de água no estado líquido nos reagentes e 5 moles de água no estado líquido nos produtos de reacção, anulam-se as 4 moles de água comuns nos reagentes e produtos, sobrando 1 mole de água nos produtos – é como se a reacção não consumisse água e formasse apenas 1 mole de água no estado líquido). Isto denomina-se "reduzir os termos semelhantes".
Para estabelecer um exemplo concreto, admita-se que se pretende saber o valor de  rHº da reacção de síntese do metano (CH4) a partir da reacção do carbono (da grafite) com o hidrogénio gasoso (H2), cuja equação química é:
rHº da reacção de síntese do metano (CH4) a partir da reacção do carbono (da grafite) com o hidrogénio gasoso (H2), cuja equação química é:
C(s) + 2H2(g) 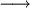 CH4(g) CH4(g) |
 rHº = ? rHº = ? |
O valor de  rHº pode ser obtido com base nas seguintes reacções:
rHº pode ser obtido com base nas seguintes reacções:
| (1) | H2(g) + ½O2(g) 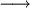 H2O(l) H2O(l) |
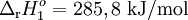 |
| (2) | C(s) + O2(g) 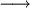 CO2(g) CO2(g) |
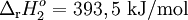 |
| (3) | CH4(g) + 2O2(g) 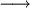 CO2(g) + 2H2O(l) CO2(g) + 2H2O(l) |
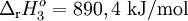 |
Para se obter a equação que se pretende, podem “somar-se” as equações (1) a (3) por aplicação de operações matemáticas como se fossem parcelas numa soma. Para efectuar a soma tem de se ter em atenção quais as espécies químicas que estão nos reagentes e produtos das equações intermediárias e na equação cujo valor de 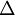 rHº é desconhecido. Para originar a equação problema, as equações intermediárias devem ser somadas da seguinte forma:
rHº é desconhecido. Para originar a equação problema, as equações intermediárias devem ser somadas da seguinte forma:
2 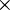 [H2(g) + ½O2(g) [H2(g) + ½O2(g) |
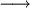 |
H2O(l)] |
C(s) + O2(g) |
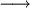 |
CO2(g) |
CO2(g) + 2H2O(l) |
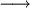 |
CH4(g) + 2O2(g) |
C(s) + 2H2(g) + |
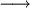 |
CH4(g) + |
Os coeficientes estequiométricos da equação (1) foram multiplicados por dois, pelo que o valor de 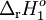 também o deve ser. O sentido da equação (3) foi invertido, pelo que se deve utilizar o valor simétrico de
também o deve ser. O sentido da equação (3) foi invertido, pelo que se deve utilizar o valor simétrico de 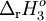
Assim,
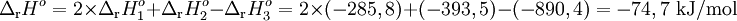 </p>
</p>
Referências
1. G. H. Hess, Pogg. Ann. 50 (1940) 385; (citado em H. M. Leicester, J. Chem. Educ. 28 (1951) 581-583).
Criada em 27 de Fevereiro de 2010
Revista em 17 de Fevereiro de 2011
Aceite pelo editor em 17 de Fevereiro de 2011

