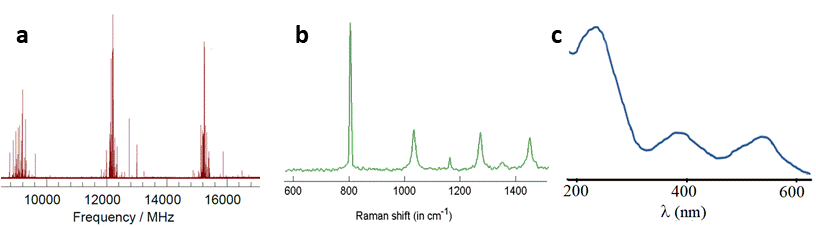
Por razões históricas e de ordem prática, diferentes tipos de espectroscopia adotaram diferentes representações convencionais, o que pode tornar a comparação entre espectros um pouco confusa. (FIGURA 1)
A radiação eletromagnética tem propriedades ondulatórias a que corresponde uma frequência (\(v\)) e um comprimento de onda (\(\lambda\)). A energia da radiação, \(E\), é proporcional à sua frequência de acordo com a equação
\(E=hv\) (1)
sendo \(h\) um valor constante universal (constante de Planck).
A velocidade da luz, \(c\), corresponde ao produto da frequência pelo comprimento de onda
\(c = ν \lambda\) (2)
e o inverso do comprimento de onda é designado por número de onda, com o símbolo \(\displaystyle {\tilde {\nu } } \)
\(\displaystyle {\tilde {\nu }}=1/\lambda\) (3)
Das equações (1-3) resulta
\(E = hc/\lambda = hc\displaystyle {\tilde {\nu }}\) (4)
Deste modo, a representação da energia da radiação de um espectro pode fazer-se com qualquer unidade de energia (\(E\)), ou qualquer grandeza que lhe seja diretamente proporcional (\(v\),\(\displaystyle {\tilde {\nu } } \)) ou inversamente proporcional (\(\lambda\)).
Tabela 1. Grandezas importantes na representação de um espectro e respetivas unidades SI.
| Grandeza | Unidade (Sistema Internacional) |
| Energia, \(E\) | \(J\) (joule) |
| Frequência, \(v\) | \(Hz\) (hertz ≡ inverso de segundo, s-1) |
| Comprimento de onda, \(\lambda\) | \(m\) (metro) |
| Número de onda, \(\displaystyle {\tilde {\nu }}\) | \(m\)-1 (inverso de metro) |
A variedade de unidades utilizadas na representação de espectros resulta da “tradição” em cada tipo de espectroscopia, que advém frequentemente das características do equipamento de deteção e da tendência natural para escolher números de fácil leitura e representação gráfica (ver TABELA 2).
Tabela 2. Intervalos de valores utilizados na representação de espectros em alguns tipos representativos de espectroscopia.
| Espectroscopia | Valores típicos | Energias correspondentes / kJ mol-1 |
| Rotacional | 10-10000 GHz | 0,004 - 4 |
| Vibracional, infravermelho | 400-4000 cm-1 | 5 - 48 |
| Eletrónica, UV-Vis | 200-700 nm | 171 - 600 |
| Fotoeletrónica | 5-20 eV | 480 - 1900 |
A utilização da energia em joule no eixo das abcissas de um espectro é muito pouco frequente. No entanto, nos casos em que a energia envolvida é elevada – como na espectroscopia eletrónica de alta energia –, é comum a utilização da energia expressa em eletrão-volt, eV.
Tradicionalmente, a espectroscopia de ultravioleta-visível (UV-Vis) utiliza a representação em função do comprimento de onda – o que tem origem histórica no facto de a dispersão da luz num prisma ser proporcional ao comprimento de onda (ver FIGURA 3 do artigo “Espectroscopia” e FIGURA 1C). Como a luz visível tem comprimentos de onda da ordem dos 10-7 m, a melhor forma de conseguir números simples, fáceis de ler, é representar o espectro de UV-Vis em nanómetros (nm): tipicamente, o eixo fica entre os 200-700 nm.
Na espectroscopia vibracional, é utilizado quase exclusivamente o número de onda, impropriamente designado por “frequência, em cm-1”. Também aqui, foi a preferência por números “simples” que determinou o uso do cm-1 como unidade: deste modo, o chamado infravermelho médio corresponde ao intervalo 400-4000 cm-1. No entanto, quando a energia da radiação já é muito afastada do visível (o chamado infravermelho longínquo), o número de onda é da ordem das dezenas de cm-1 e é comum a utilização da frequência em Terahertz (1 THz ≈ 33 cm-1). Na espectroscopia de Raman, representa-se o desvio entre a energia da luz incidente e difundida no intervalo 0-4000 cm-1 (FIGURA 1B). A título de curiosidade, refira-se que os espectros de difusão inelástica de neutrões são por vezes representados em função da energia dos neutrões, medida em milieletrões-volt, meV.
A convenção para a espectroscopia rotacional é utilizar a grandeza frequência, em gigahertz (GHz, FIGURA 1A) ou, alternativamente, em megahertz (MHz).
A espectroscopia de ressonância magnética nuclear (RMN) é um caso à parte, porque a separação entre os níveis de energia da amostra depende do campo magnético aplicado pelo espectrómetro – ou seja, não é independente do aparelho de medida, como é no caso dos níveis eletrónicos, vibracionais ou rotacionais. Por esse motivo, não faz sentido referir o valor absoluto da energia absorvida numa transição e em vez disso representa-se o desvio relativo a um composto de referência medido nas mesmas condições. Este desvio é designado por desvio químico, δ, e representado em partes por milhão, ppm.
Os livros dedicados aos temas de espectroscopia incluem frequentemente uma tabela de conversão entre unidades de “energia”, ou seja, unidades de grandezas diretamente proporcionais à energia (TABELA 2). Esta tabela permite converter rapidamente 1 cm-1 em eV ou kJmol-1. O mesmo tipo de conversão pode ser obtido de forma ainda mais eficiente em conversores “on-line”.
Tabela 3. Fatores de conversão entre unidades de grandezas diretamente proporcionais.
| J/mol | eV | cm-1 | GHz | |
| J/mol | 1 | 1.03643×10-5 | 8.35935×10-2 | 2.50607 |
| eV | 9.64853×104 | 1 | 8.06554×103 | 2.41799×105 |
| cm-1 | 11.9627 | 1.23985×10-4 | 1 | 29.9792 |
| GHz | 0.399031 | 4.13567×10-6 | 0.0333564 | 1 |
BIBLIOGRAFIA
- 1 Teixeira Dias, J. J. C., Espectroscopia Molecular: Fundamentos, Métodos e Aplicações, Edição: Fundação Calouste Gulbenkian, 1986, ISBN: 0066000107119
- 2 Hollas, J. M., High Resolution Spectroscopy, Edição: Butterworth-Heinemann, 1982, ISBN: 9780471974215.
- 3 Claro, P.R., Espectroscopia. Rev. Ciência Elem., V5(4):052, 2017.
- 4 Tabela de conversão. (acedido em 1 de outubro de 2018).
Recursos relacionados disponíveis na Casa das Ciências:
Criada em 9 de Setembro de 2018
Revista em 21 de Setembro de 2018
Aceite pelo editor em 4 de Outubro de 2018


