Energia de activação
Referência : Lima, L.S., (2015) Energia de ativação, Rev. Ciência Elem., V3(2):035
Autor: Luis Spencer Lima
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2015.035]

Designa-se por energia de activação (símbolo Ea) a energia mínima necessária para que as espécies reagentes iniciem uma reacção química. Alternativamente, e de acordo com a teoria do estado de transição, a energia de activação corresponde à diferença de energia entre os reagentes e o complexo activado, que é uma estrutura intermediária na conversão de reagentes e produtos e que corresponde ao ponto de energia potencial máxima ao longo da coordenada reaccional.
O conceito de energia de activação foi introduzido em 1889 pelo físico e químico sueco Svante Arrhenius no âmbito dos seus estudos em cinética química. É um parâmetro com uma forte influência na velocidade das reacções, pois quanto maior for a energia de activação, mais lenta é a reacção (para uma dada temperatura). A equação que traduz a variação da velocidade específica (k) com a temperatura absoluta (T) e a energia de activação é a denominada equação de Arrhenius.

Nesta equação, R representa a constante dos gases e A designa-se por factor pré-exponencial ou factor de frequência, estando relacionado com a frequência de colisões entre moléculas de reagentes e com a sua orientação. Tem as mesmas unidades que k. Apesar do seu nome, esta equação foi proposta pela primeira vez em 1884 pelo químico holandês Jacobus van’t Hoff. No entanto, foi Arrhenius quem apresentou uma explicação física e a interpretou. Arrhenius alegou que, para os reagentes se transformarem em produtos, era necessário que os primeiros adquirissem uma quantidade de energia mínima, a energia de activação (Ea). Para uma dada temperatura, a fracção de moléculas que têm uma energia cinética superior a Ea pode ser calculada através da distribuição de Maxwell-Boltzmann ou através da mecânica estatística. Esta fracção é proporcional a exp[-Ea/(RT)].
Esta equação é muito importante no campo da cinética, pois permite a determinação da energia de activação de uma reacção após a determinação da velocidade específica a várias temperaturas. A logaritmização da equação (1) resulta na seguinte equação
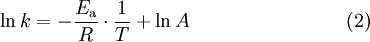
Assim, verificando-se a equação de Arrhenius, a representação gráfica de ln(k) em função de 1/T é numa linha recta com declive igual a –Ea/R e ordenada na origem igual a ln(A).
Uma das formas mais importantes de acelerar uma reacção química é através da adição de um catalisador. Ao contrário do que é muitas vezes afirmado, o catalisador não diminui a energia de activação da reacção não catalisada. O que acontece é que o catalisador fornece um caminho alternativo para os reagentes se converterem em produtos, através de uma sequência de passos que envolvem uma energia de activação consideravelmente menor, o que faz com que a reacção ocorra mais rapidamente (ver figura 1). A nível biológico, as reacções associadas ao metabolismo são aceleradas por acção de catalisadores especiais denominados enzimas, cujos mecanismos de reacção envolvem uma energia de activação muito inferior à da reacção não catalisada.
Criada em 06 de Março de 2010
Revista em 06 de Fevereiro de 2011
Aceite pelo editor em 08 de Fevereiro de 2011
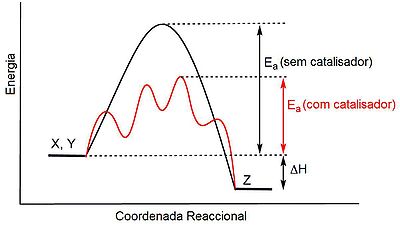
 Z com e sem catalisador.
Z com e sem catalisador.
