Referência : Lage, E., (2021) Eletrostática, Rev. Ciência Elem., V9(1):015
Autor: Eduardo Lage
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2021.015]

---

[editar] Resumo

A eletrostática é dedicada ao estudo do campo elétrico originado por cargas em repouso. Começa-se por considerar o campo gerado por uma única carga, generalizando-se, depois a um número arbitrário de cargas, distribuídas continuamente ou uma colecção discreta. A grandes distâncias de uma tal distribuição, a expansão multipolar fornece um desenvolvimento do potencial elétrico em termos de momentos dipolares, quadrupolares, etc., conceitos importantes no estudo de núcleos atómicos, moléculas, cristais líquidos… A análise da energia eletrostática do campo permite, por um lado, definir a energia de interação entre distribuições de carga bem separadas e, por outro lado, obter as forças e momentos que se exercem sobre essas distribuições. De fora deste trabalho ficam os fenómenos de influência elétrica que serão considerados noutro artigo.

O campo gerado por uma carga pontual

Considere-se uma carga pontual ($q_{1}$), imóvel, e escolha-se um referencial cartesiano fazendo coincidir a sua origem com a posição da carga. O potencial elétrico^[1] gerado pela carga só depende, por simetria, da distância ($r$) desta ao ponto de observação, i.e., $\varphi \left ( r \right )$. Assim, o campo elétrico $\vec{E}=-\bigtriangledown \varphi$ é puramente radial^[2]: $E_{r}\left ( r \right )=-\frac{d\varphi }{dr}$. Considere- -se, agora, uma esfera centrada na carga e raio $r$. Aplicando a forma integral da equação de Maxwell-Coulomb, tem-se:

$E_{r}4\pi r^{2}=\frac{q_{1}}{\varepsilon _{0}}$ (1)

Donde:

$\frac{d\varphi }{dr}=-\frac{q_{1}}{4\pi\varepsilon _{0}r^{2}}\; \; \; \; \; \varphi \left ( r \right )=\frac{q_{1}}{4\pi\varepsilon _{0}r}$ (2)

Aqui, a constante arbitrária que se poderia adicionar ao potencial, é nula porque se convenciona ser $\varphi \xrightarrow[r\rightarrow \infty ]{}0$.

Mantendo o referencial fixo, pode agora obter-se a expressão do campo para uma posição arbitrária $\left ( \vec{r}_{1} \right )$ da carga. Designando por $\vec{r}$ a posição do mesmo ponto de observação, então a distância deste ponto à carga é $\left | \vec{r}-\vec{r}_{1} \right |$, pelo que se escreve:

$\varphi \left ( \vec{r} \right )=\frac{1}{4\pi\varepsilon _{0}}\frac{q_{1}}{\left | \vec{r}-\vec{r}_{1} \right |}$ (3)

$\vec{E}\left ( \vec{r} \right )=-\bigtriangledown \varphi =\frac{q_{1}}{4\pi \varepsilon _{0}}\frac{\vec{r}-\vec{r}_{1}}{\left | \vec{r}-\vec{r}_{1} \right |^{3}}$ (4)

O campo para uma distribuição arbitrária de cargas

Partindo da eq. (3), é imediato obter o potencial para um conjunto arbitrário de $N$ cargas por simples sobreposição dos potenciais gerados por cada uma:

$\varphi \left ( \vec{r} \right )=\sum_{i=1}^{N}\frac{1}{4\pi\varepsilon _{0}}\frac{q_{i}}{\left | \vec{r}-\vec{r}_{i} \right |}$ (5)

Esta expressão adapta-se facilmente a distribuições contínuas substituindo a soma pelo integral adequado. Para uma distribuição em volume, tem-se:

$\varphi \left ( \vec{r} \right )=\frac{1}{4\pi\varepsilon _{0}}\int_{}^{}dV'\frac{\rho \left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r} \right |}$ (6)

onde $\rho \left ( \vec{r} \right )$ é a densidade volúmica de carga. Este potencial é, pois, a solução particular da equação de Poisson:

$\Delta\varphi =-\frac{\rho }{\varepsilon _{0}}$ (7)

[No Apêndice, é discutida a forma analítica da densidade de carga para uma carga pontual cujo potencial é dado pela eq. (3)].

A eq. (6) adapta-se facilmente a distribuições em superfícies ou linhas, bastando lembrar que o integral é uma soma dos potenciais gerados pelas cargas $\delta Q\left ( \vec{r} \right )=\rho \left ( \vec{r} \right )dV$. Os exemplos seguintes ilustram estas observações; neles faz-se uso, apenas, da forma integral da equação de Maxwell-Coulomb^[3].

a) Distribuição uniforme numa esfera (raio $a$, carga $Q$)

Por simetria, o campo elétrico tem a direcção radial e só depende da distância ao centro da esfera (FIGURA 1). Tem-se:

$r>a\; \; \; E_{r}4\pi r^{2}=\frac{Q}{\varepsilon _{0}}\; \; \; \rightarrow \; \; \;E_{r}=\frac{Q}{4\pi\varepsilon _{0}}\frac{1}{r^{2}}$

$r<\textit{a} \; \; \; E_{r}4\pi r^{2}=\frac{1}{\varepsilon _{0}}\frac{Q}{\frac{4}{3}\pi a^{3}}\frac{4}{3}\pi r^{2\; \; \; \rightarrow }\; \; \; E_{r}=\frac{Q}{4\pi \varepsilon _{0}}\frac{r}{a^{3}}$ (8)

O correspondente potencial elétrico deduz-se por integração de $E_{r}\left ( r \right )=-\frac{d\varphi }{dr}$, sendo contínuo na superfície da esfera:

$r>a\; \; \; \varphi \left ( r \right )=\frac{Q}{4\pi \varepsilon _{0}}\frac{1}{r}$

$r<\textit{a} \; \; \; \varphi \left ( r \right )=\frac{Q}{8\pi \varepsilon _{0}a}\left ( 3-\frac{r^{2}}{a^{2}} \right )$ (9)

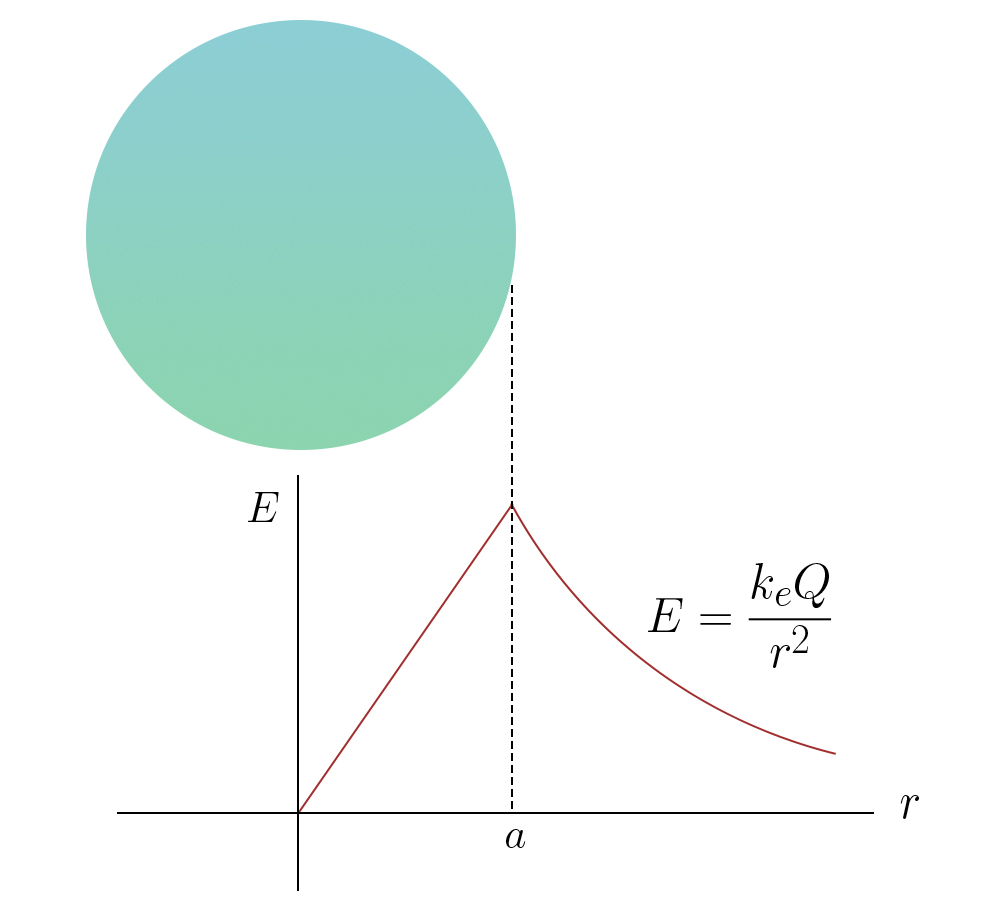
Se a carga se distribuir apenas na superfície da esfera, o campo elétrico é nulo no seu interior e, no exterior, é definido pela primeira equação em (8); quanto ao potencial elétrico, tem a forma da primeira equação em (9), sendo constante no interior com o valor $\varphi =\frac{Q}{4\pi \varepsilon _{0}}\frac{1}{a}$.

b) Distribuição uniforme numa superfície plana (densidade superficial de carga $\rho s$)

O campo elétrico reduz-se, por simetria, à sua componente $E_{z}$ perpendicular ao plano; não havendo cargas acima ou abaixo do plano, então $\frac{\partial E_{z}}{\partial z}=0$, i.e., $E_{z}$ é uniforme naquelas regiões. A simetria de reflexão no plano determina que esta componente tem sinais opostos acima e abaixo do plano. Considere-se, então, um pequeno cilindro reto, com área das bases $\delta A$, cortado a meio pelo plano (cilindro gaussiano). Aplicando a forma integral de Maxwell-Coulomb, obtém-se:

$E_{z}\delta A-\left ( -E_{z} \right )\delta A=\frac{\rho_{S} \delta A}{\varepsilon _{0}}\rightarrow E_{z}=\frac{\rho_{S}}{2\varepsilon _{0}}$ (10)

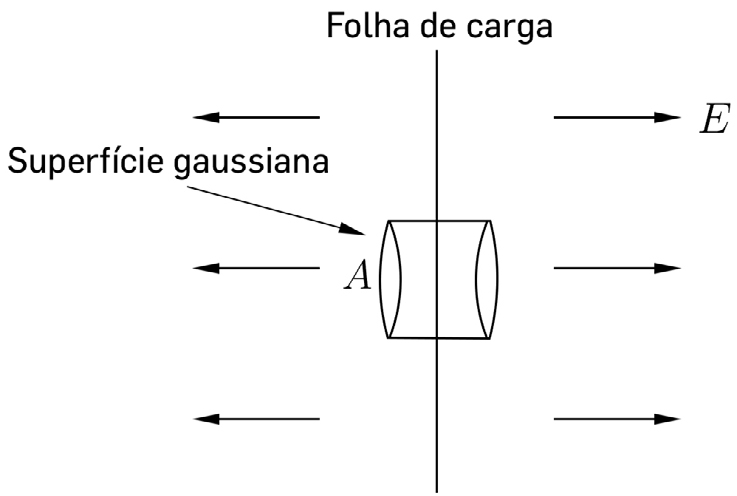
Este resultado é mais geral do que a sua dedução fará parecer. Com efeito, para cargas distribuídas, não necessariamente de modo uniforme, sobre uma qualquer superfície, a eq. (10) é válida na imediata vizinhança dos pontos da superfície (sendo, agora, $E_{z}$ a componente normal à superfície nesses pontos). Com efeito, se se considerar um pequeno elemento da superfície de área $\delta A$, esse elemento aparecerá plano quanto mais próximo dele se estiver. Deste modo, se $\vec{E}$ for o campo total, gerado quer pelas cargas na superfície quer por outras cargas fora dela), a descontinuidade da componente normal deste campo é devida unicamente às cargas na superfície, podendo ser obtida pela eq. (10); por outro lado, a componente contínua do campo é devida às outras cargas e pode ser obtida efectuando a semi-soma dos seus valores de um e outro lado da superfície. Este comentário é importante para o cálculo das forças que o campo exerce sobre cargas distribuídas superficialmente.

c) O condensador plano

Considerem-se dois planos paralelos (distantes $a$), tendo o plano da esquerda (FIGURA 3) densidade de carga $\rho _{S}$ e o da direita $- \rho _{S}$; o eixo $z$ é perpendicular aos planos. Por sobreposição dos campos originados por cada plano, obtém-se:

$E_{z}=0$ no exterior dos planos

$E_{z}=\frac{\rho _{S}}{\varepsilon _{0}}$ entre os planos

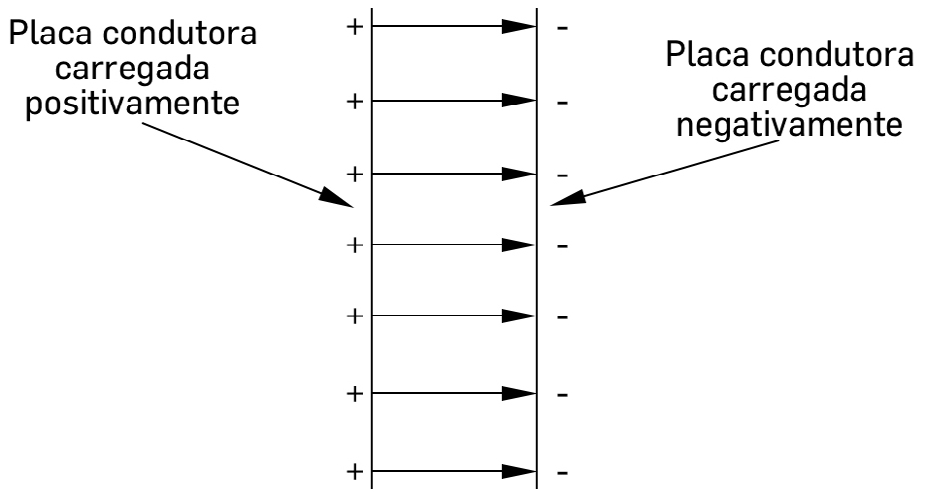
Há, assim, uma diferença de potencial elétrico $V$ entre os dois planos; arbitrando $\varphi =0$ para o plano da direita, tem-se:

$V=E_{z}a=\frac{\rho _{s}a}{\varepsilon _{0}}$

Este exemplo fornece um modelo aproximado para um condensador plano, onde as placas, agora finitas, têm área $A$. Designa-se por carga do condensador a carga na placa positiva.

Assim, numa boa aproximação, é $Q=\rho _{S}A$ e, portanto, $V=\frac{\varepsilon _{0}A}{a}Q$. A capacidade do condensador é a sua carga para uma diferença de potencial de $1V$, i.e.,

$C=\frac{Q}{V}=\frac{\varepsilon _{0}A}{a}$ (11)

A unidade da capacidade no S.I. é o farad ($F$).

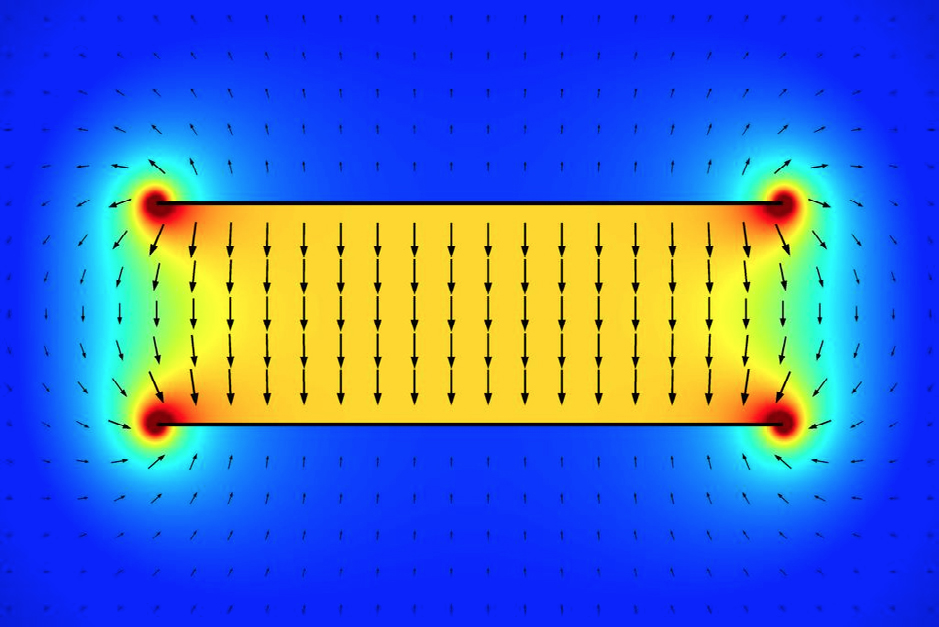
Note-se, porém, que para um real condensador plano, não só há uma acumulação de carga junto aos bordos das placas como o campo deixa de ser uniforme nas proximidades destes bordos e existem linhas de força no exterior das placas (FIGURA 4). Na verdade, um condensador plano, observado de longe, é um dipólo elétrico.

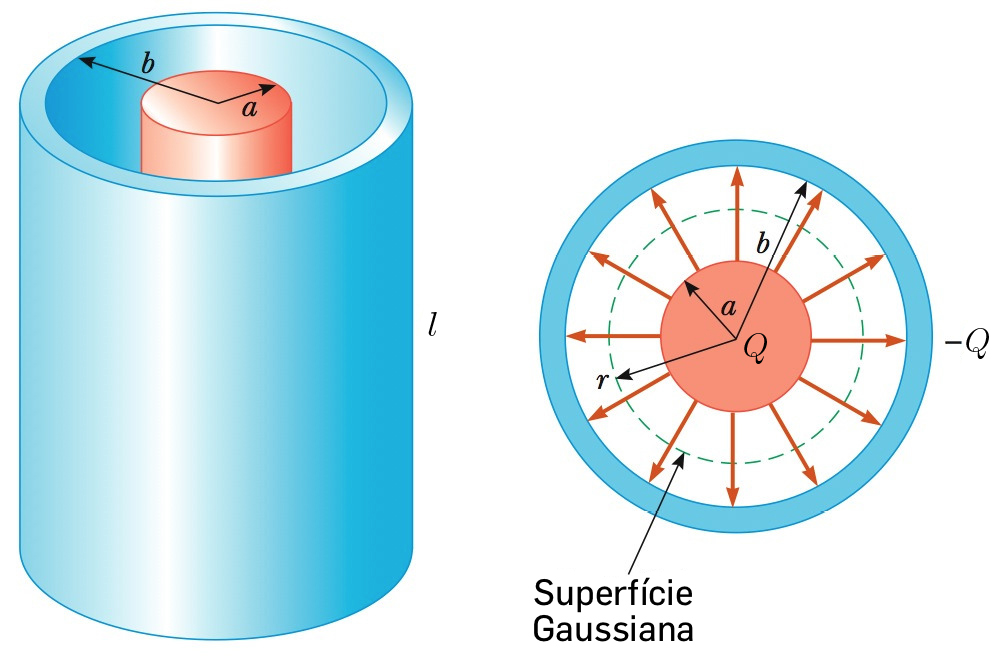
Considerem-se dois cilindros coaxiais, comprimento $l$, secção recta circular, de raios a e $b > a$. Uma bateria estabelece uma diferença de potencial $V$ entre os cilindros, ficando o exterior ao potencial 0. A bateria faz passar carga $Q$ do cilindro exterior para o cilindro interior - é essa a carga do condensador. Ignorando o efeito dos bordos, o campo está confinado ao espaço entre cilindros e tem a direcção radial. Imaginando um cilindro gaussiano, coaxial com os dados, de raio $r$ com a $a < r < b$, o fluxo do campo através deste cilindro é $E_{r}2 \pi rl$ que, pela lei de Maxwell-Coulomb deve ser igual a $\frac{Q}{\varepsilon _{0}}$. Então:

$E_{r}=\frac{Q}{2\pi \varepsilon_{0}}\frac{1}{lr}$. Deste modo, a diferença de potencial entre os cilindros é:

$V=\int_{a}^{b}drE_{r}=\frac{Q}{2\pi \varepsilon _{0}l}log\left ( \frac{b}{a} \right )$

A capacidade do condensador cilíndrico é:

$C=\frac{Q}{V}=2\pi\varepsilon _{0}\frac{l}{log\left ( \frac{b}{a} \right )}$ (12)

A expansão multipolar do potencial

Considere-se uma distribuição de carga localizada numa região limitada do espaço, de extensão típica $a$ - por exemplo, um núcleo atómico ou uma molécula. Como se comporta o potencial elétrico em pontos distantes dessa região $\left ( r\gg a \right )$? A resposta é a expansão multipolar, i.e., o desenvolvimento do potencial em potências de $\frac{a}{r}$. Para isso, escolhe-se um ponto qualquer no interior da distribuição para origem do sistema de coordenadas. Deste modo, a densidade de carga distribui-se em torno da origem até à distância típica $a$. Então, na eq. (6), o termo dominante no denominador é $r=\left | \vec{r} \right |$ e obtém-se a expansão fazendo o desenvolvimento de $\left | \vec{r}-\vec{r}' \right |^{-1}$ em potências de $\frac{r'}{r}\sim \frac{a}{r}$. Até à 2ª ordem (nesta quantidade), tem-se:

$\frac{1}{\left | \vec{r}-\vec{r} \right |}=\left ( r^{2}-2\vec{r}\cdot \vec{r}'+r^{'2} \right )^{-\frac{1}{2}}=\frac{1}{r}\left ( 1-\frac{2\vec{r}\cdot \vec{r}}{r^{2}}+\frac{r^{'2}}{r^{2}} \right )^{-\frac{1}{2}}=$

$=\frac{1}{r}\left [ 1+\frac{\vec{r}\cdot\vec{r}'}{r^{2}}+\frac{3}{2}\left ( \frac{\vec{r}\cdot\vec{r}'}{r^{2}} \right )^{2}-\frac{1}{2}\frac{r^{'2}}{r^{2}}+... \right ]$

Inserindo na eq. (6), obtém-se:

$4\pi \varepsilon _{0}\varphi \left ( \vec{r} \right )=\frac{1}{r}\int dV'\rho \left ( \vec{r'} \right )\left [ 1+\frac{\vec{r}\cdot\vec{r'}}{r^{2}}+\frac{3}{2}\left ( \frac{\vec{r}\cdot \vec{r}}{r^{2}} \right )^{2}-\frac{r'^{2}}{2r^{2}}+... \right ]$

No segundo membro, o primeiro termo faz intervir a carga total da distribuição:

$Q=\int dV'\rho \left ( \vec{r'} \right )$

O segundo termo faz intervir o momento dipolar elétrico da distribuição, o vetor:

$\vec{p}=\int dV'\rho \left ( \vec{r}' \right )\vec{r}'$ (13)

Os últimos dois termos fazem intervir o momento quadrupolar da distribuição, um tensor simétrico de 2ª ordem^[4]:

$D_{ij}=\frac{1}{2}\int dV'\rho \left ( \vec{r}' \right )\left [ 3x'_{i}x'_{j}-r'^{2}\delta _{ij} \right ]$ (14)

Note-se que o traço deste tensor é nulo:

$D_{ij}=0$ (15)

Assim, a expansão do potencial escreve-se (soma sobre índices repetidos):

$4\pi \varepsilon _{0}\varphi \left ( \vec{r} \right )=\frac{Q}{r}+\frac{\vec{p}\cdot \vec{r}}{r^{3}}+\frac{1}{3}D_{ij}\frac{3x_{i}x_{j}-r^{2}\delta _{ij}}{r^{5}}+...$ (16)

Aqui, no último termo, adicionou-se um fator que é, na verdade, nulo pela eq. (15).

Alguns comentários:

a) Para grandes distâncias da distribuição de carga, o termo dominante é o primeiro, o potencial de Coulomb como se toda a carga estivesse localizada na origem do referencial escolhido. É, muitas vezes, este termo que é apenas utilizado como potencial experimentado por eletrões movendo-se em torno de núcleos atómicos ou para interações entre iões.

b) Se a carga total da distribuição for nula (átomos ou moléculas neutras), o termo dominante é o segundo, i.e., a contribuição dipolar. Tal termo decai como $\frac{1}{r^{2}}$ e exibe anisotropia porque depende da posição do ponto de observação (i.e., $\vec{r}$) em relação ao momento dipolar. O campo elétrico associado a tal termo mostra claramente esta anisotropia:

$\vec{E}\left ( \vec{r} \right )=\frac{1}{4\pi\varepsilon _{0}}\frac{3\vec{r}\left ( \vec{p}\cdot\vec{r} \right )-r^{2}\vec{p}}{r^{5}}$ (17)

Para duas cargas pontuais de sinais opostos, a definição elementar do momento dipolar coincide com o resultado expresso na eq. (13) - basta substituir o integral por soma sobre as cargas e $pdV\rightarrow q$ para cada carga. Assim, se $\vec{l}$ for o vetor de posição da carga positiva ($+q$) em relação à negativa ($−q$), obtém-se:

$\vec{p}=q\vec{l}$ (18)

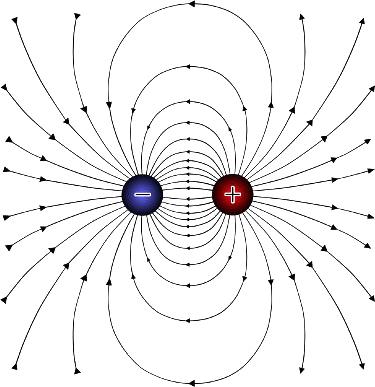
A FIGURA 6 exibe as linhas de força do campo elétrico gerado por um tal dipólo ideal.

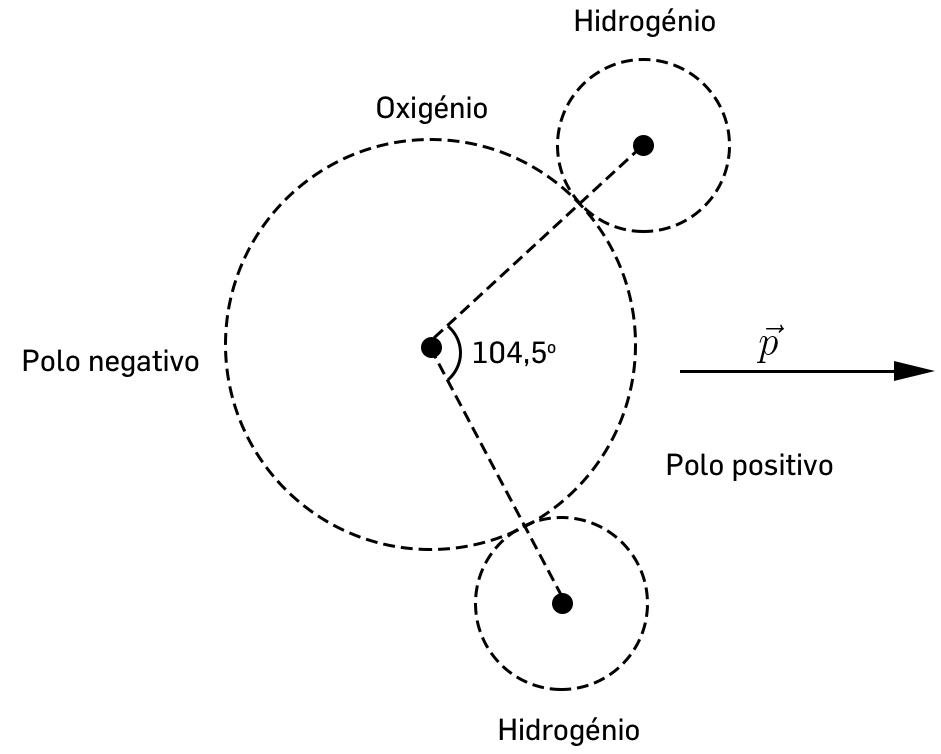
Por exemplo, na molécula da água (H₂O), o oxigénio ocupa o centro de um tetraedro e possui carga $-2q_{e}$ ($q_{e}$ é o valor absoluto da carga do eletrão), enquanto que cada hidrogénio (carga ($q_{e}$) ocupa um dos vértices do tetraedro; a molécula é neutra, mas apresenta um momento dipolar (FIGURA 7) de grande importância para as propriedades químicas e biológicas da água. Mais adiante mostra-se como se pode verificar a existência deste dipólo com uma experiência simples.

c) O termo quadrupolar na eq. (16) será dominante se a distribuição de carga apresentar carga total e momento dipolar nulos., como acontece nas moléculas de cristais líquidos, ou como correcção ao potencial coulombiano se apenas o momento dipolar for nulo, como acontece com o potencial gerado por núcleos atómicos no estado fundamental. Neste último caso, o momento quadrupolar do núcleo é sentido pelos electrões que o orbitam, originando o levantamento de degenerescências nos níveis atómicos, assim fornecendo, também, informação sobre a distribuição de carga no núcleo.

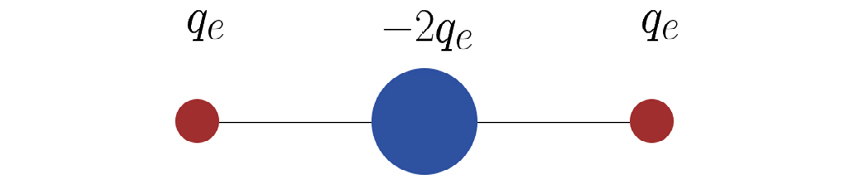
A FIGURA 8 representa, esquematicamente, a distribuição de carga no átomo de oxigénio - o núcleo (azul) é tomado como origem e os dois eletrões (vermelho) situam-se simetricamente em relação àquele, à distância $a$. Tomando o eixo $x$ na linha das cargas, é fácil obter:

$D_{11}=-2q_{e}a^{2}\; \; \; \; \; D_{22}=D_{33}=q_{e}a^{2}$

sendo nulos todos os outros termos.

Energia eletrostática

Qualquer configuração de cargas tem associada uma energia $U_{e}$^[5]: a sua diferença entre uma configuração inicial e outra final é o simétrico do trabalho realizado pelas forças do campo para levar as cargas da primeira à segunda configurações:

$-dU_{e}=\delta W$ (19)

Esta energia tem a expressão:

$U_{e}=\int dV\frac{\varepsilon _{0}\vec{E}^{2}}{2}$ (20)

Observe-se que a energia eletrostática está localizada em todo o espaço e não, apenas, na região onde existam cargas. Uma outra expressão equivalente revela-se útil para o cálculo da energia eletrostática em diversas situações. Com efeito:

$U_{e}=\int dV\frac{\varepsilon _{0}}{2}\vec{E}^{2}=-\int dV\frac{\varepsilon _{0}}{2}\vec{E}\bigtriangledown \varphi =-\int dV\frac{\varepsilon _{0}}{2}\bigtriangledown \cdot \left ( \vec{E}\varphi \right )+\int dV\frac{\varepsilon _{0}}{2}\varphi \bigtriangledown \cdot \vec{E}$

O penúltimo termo é nulo porque, pelo teorema de Gauss pode ser convertido num fluxo através de uma superfície esférica de raio $R$ arbitrariamente grande: $\int_{\Sigma }^{}dS\varphi \vec{E}\cdot \vec{n}$. Ora, muito longe das cargas é $\varphi \sim \frac{1}{R}$ e $\vec{E} \sim \frac{1}{R^{2}}$, pelo que tal integral decai como $\frac{1}{R}$. Quanto ao último termo da expressão anterior, a equação de Maxwell-Coulomb conduz à forma pretendida:

$U_{e}=\frac{1}{2}\int dV\rho \varphi$ (21)

Exemplos.

a) Distribuição uniforme de carga numa esfera

Usando a eq. (9), com a densidade $\rho =Q/\left ( \frac{4\pi}{3}R^{3} \right )$, facilmente se obtém:

$U_{e}=\frac{3}{5}\frac{Q^{2}}{4\pi \varepsilon _{0}R}$ (22)

Note-se que esta energia diverge para uma carga pontual.

Se a carga estiver, apenas, distribuída uniformemente na superfície da esfera, o resultado é, ainda, mais simples de obter:

$U_{e}=\frac{Q^{2}}{8\pi \varepsilon _{0}R}$ (23)

O raio clássico do eletrão $\left ( r_{e} \right )$ é o raio de uma tal esfera com a carga do eletrão $\left ( -q_{e} \right )$ de modo que a energia eletrostática iguala metade da energia em repouso do eletrão:

$\frac{q_{e}^{2}}{4\pi \varepsilon _{0}r_{c}}=m_{e}c^{2}\; \; \; \; \; \rightarrow \; \; \; \; \; r_{c}=8,82...fm$ (24)

Nota: um fermi $\left ( fm \right )=10^{-5} A^{\circ} =10^{-13}$cm

Este raio clássico é uma quantidade útil porque intervém em muitas expressões de Física Atómica, mas não deve levar a pensar que o eletrão tenha qualquer geometria esférica.

A eq. (21) é facilmente adaptada a cargas pontuais, bastando substituir $dV\rho \rightarrow q_{i}$ e o integral pela soma sobre as cargas:

$U_{e}=\frac{1}{2}\sum_{i}^{}q_{i}\varphi \left ( \vec{r}i \right )=\frac{1}{2}\sum_{i\neq j}^{}\frac{q_{i}q_{j}}{4\pi \varepsilon _{0}\left | \vec{r}_{i}-\vec{r}_{j} \right |}$ (25)

Aqui, eliminaram-se os termos de auto-energia $\left ( i=j \right )$ que são divergentes. Note-se que apenas diferenças de energia eletrostática determinam o trabalho das forças (eq. (19)), pelo que tais termos são eliminados automaticamente.

Como exemplo, considere-se a energia eletrostática de um núcleo atómico com $Z$ prótões e $A − Z$ neutrões ($A$ é o número de massa, i.e., o número de nucleões). Os prótões são todos equivalentes, pelo que se pode reescrever a eq. (25) sob a forma:

$U_{e}=\frac{Z}{2}\sum_{i\neq 1}^{}q_{1}\varphi _{1}\left ( \vec{r}_{1} \right )\simeq \frac{Z}{2}\int dV\rho _{1}\varphi _{Z-1}$

Aqui, $\varphi _{1}\left ( \vec{r}_{1} \right )$ é o potencial originado pelos prótões $i\neq 1$ sobre o prótão selecionado. A última expressão traduz a média sobre a posição de todos os prótões face às suas grandes velocidades que os levam a, praticamente, ocupar uniformemente o volume do núcleo. Assim, $\rho _{1}\approx \frac{q_{e}}{\frac{4\pi}{3}R^{3}}$ e $\varphi _{Z-1}$ é o potencial de uma esfera (raio $R$) com uma carga $\left ( Z-1 \right )q_{e}$ uniformemente distribuída, o que permite utilizar-se o resultado da eq. (9). Deste modo, obtém-se:

$U_{e}=\frac{3}{5}\frac{Z\left ( Z-1 \right )q_{e}^{2}}{4\pi \varepsilon _{0}R}$

O raio de um núcleo é essencialmente determinado pelo seu número de massa $R\approx A^{\frac{1}{3}}$ (expresso em $fm$) - tal significa uma densidade nuclear $\frac{A}{R^{3}}$ praticamente constante, tal como uma gota de liquido. Esta energia eletrostática é enorme: na tabela abaixo estimam- -se os seus valores para os núcleos de oxigénio ($O$) e urânio ($U$):

Os núcleos são mantidos estáveis porque, sobrepostas às forças repulsivas entre os prótões, existem forças atrativas ainda de maior grandeza entre todos os nucleões – são as forças nucleares e, ao contrário das eletrostáticas, atuam apenas a curtas distâncias (da ordem de $1fm$), entre os vizinhos mais próximos (tornam-se repulsivas a mais curtas distâncias, tal como as forças de van der Waals entre moléculas). A contribuição desta energia nuclear é, então, proporcional ao número de nucleões e pode estimar-se o seu valor porque o urânio encontra-se no limite de estabilidade (é radioativo, mas com uma vida média muito longa!), i.e., a contribuição atrativa das forças nucleares é da ordem da contribuição repulsiva eletrostática - na verdade, compensa não só esta, mas também a energia cinética dos nucleões que tenderia a dispersa-los e que é da ordem da energia eletrostática. Designando por $\varepsilon$ a energia nuclear por nucleão, será, então, para o urânio, $A\varepsilon \sim$2,2GeV , donde $\varepsilon \approx$9,2MeV.

Vê-se, agora, por que o núcleo de oxigénio é bastante estável: as forças nucleares contribuem com 16$\varepsilon \sim$148MeV , bem acima dos 18,1MeV da energia eletrostática. E vê- -se, também, por que o U235 se desintegra: tem a mesma carga do U238, mas menos 3 neutrões e, portanto, a energia de coesão das forças nucleares não vence a repulsão eletrostática.

b) O condensador plano

Usando a eq. (21), facilmente se encontra a energia eletrostática para um condensador plano:

$U_{e}=\frac{1}{2}QV=\frac{Q^{2}}{2C}=\frac{CV^{2}}{2}$ (26)

onde $C$ é a capacidade do condensador, eq. (11).

Qual a força que atua na placa negativa? Esta força tem, evidentemente, a direção do eixo $z$ (FIGURA 3) e poder-se-ia pensar que seria $F_{z}=-QE_{z}$. Porém, esta conclusão está errada. Com efeito, o campo $E_{z}$ é a sobreposição dos campos originados pelas cargas nas duas placas. É óbvio que a força na placa negativa se deve, apenas, às cargas na placa positiva; ora estas criam um campo $\frac{1}{2}E_{z}$, a parte contínua do campo quando se atravessa a placa negativa. Assim, é $F_{z}=-\frac{1}{2}QE_{z}=-\frac{1}{2}Q\frac{V}{a}=-\frac{1}{2}\frac{Q^{2}}{aC}$, onde $a$ é a distância entre as placas. Este resultado pode ser confirmado usando a energia eletrostática. Para isso, imagine-se um deslocamento da placa negativa de modo que $a\rightarrow a+\delta a$, mantendo as mesmas cargas nas placas. O trabalho realizado pelo campo é $\delta W=F_{z}\delta a$; usando a eq. (19), tem-se:

$F_{z}\delta a=-dU_{e}=-d\left ( \frac{Q^{2}}{2C} \right )=\frac{Q^{2}}{2C^{2}}\delta C$

Ora, pela eq. (11), é $\delta C=-\frac{\varepsilon _{0}A}{a^{2}}\delta a=-\frac{C}{a}\delta a$, obtendo-se, assim, $F_{z}=-\frac{Q^{2}}{2Ca}$.

Este assunto merece algumas considerações adicionais.

O circuito da FIGURA 9 mostra o condensador e a bateria que serviu para o carregar. É óbvio que a força que se exerce na placa negativa é a que atrás se obteve. A energia eletrostática escreve-se, em função dos dados, $U_{e}=\frac{1}{2}CV^{2}$. Suponha-se que se procede ao mesmo deslocamento $\delta a$ da placa negativa, mas mantendo, agora, a mesma diferença de potencial, i.e., bateria ligada. Um uso descuidado da eq. (19) leva a uma conclusão errada. Com efeito, parece que:

$\delta W=F_{z}\delta a=-dU_{e}=-\frac{1}{2}V^{2}\frac{dC}{da}\delta a\; \; \; \; \; \rightarrow \; \; \; \; \; F_{z}=\frac{CV^{2}}{2a}$

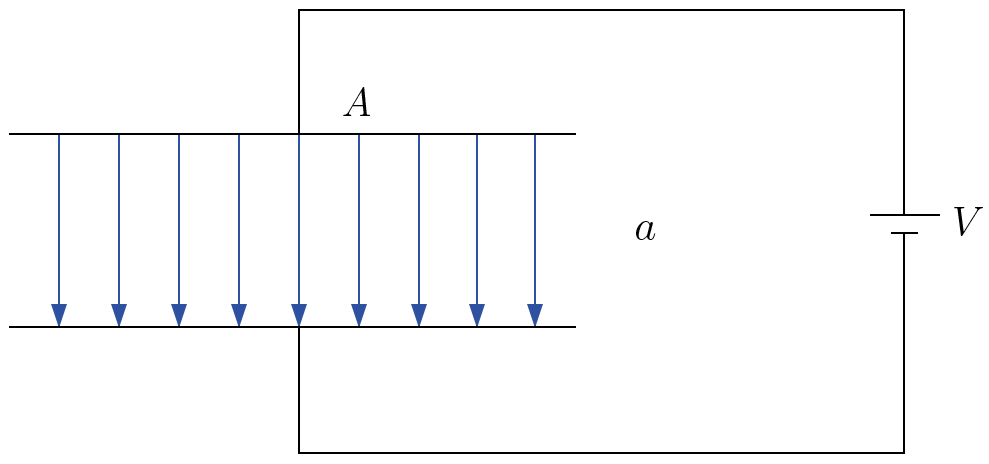
Resultado que coincide com o anterior em valor absoluto, mas com o sinal errado! Onde está o erro? O trabalho $\delta W$ realizado pelo campo não é apenas $F_{z}\delta a$. Com efeito, como é mantida a diferença de potencial entre as placas durante o deslocamento, a carga do condensador variou: $\delta Q=V\delta C$. Tal carga foi transportada da placa positiva para a negativa – teve, pois, que passar do cátodo para o ânodo na bateria. O trabalho realizado pelo campo no interior da bateria (igual e oposto ao realizado pela força-eletromotriz da bateria) foi $-V\delta Q=-V^{2}\delta C$. Assim, $\delta W=F_{z}\delta a-V^{2}\delta C$. Com esta correção, tem-se:

$\delta W=F_{z}\delta a-V^{2}\delta C=-dU_{e}=\frac{1}{2}V^{2}\delta C\rightarrow F_{z}=\frac{1}{2}V^{2}\frac{dC}{da}=-\frac{CV^{2}}{2a}$

em completo acordo com o resultado obtido quando as cargas permaneciam constantes. Estas considerações aplicam-se a qualquer tipo de condensador, seja qual for a sua geometria.

Expansão multipolar da energia eletrostática

Imaginem-se duas distribuições de carga bem definidas e distintas (o núcleo e a nuvem eletrónica, duas moléculas, etc.) que serão designadas por $\rho _{1}$ e $\rho _{2}$ e que geram os respetivos potenciais $\varphi _{1}$ e $\varphi _{2}$. A energia eletrostática para o conjunto das duas distribuições obtém-se da eq. (21):

$U_{e}=\frac{1}{2}\int dV\left ( \rho _{1}+\rho _{2} \right )\left ( \varphi _{1}+\varphi _{2} \right )=\frac{1}{2}\int dV\left ( \rho _{1}\varphi _{1}+\rho _{2}\varphi _{2}+\rho _{1}\varphi _{2}+\rho _{2}\varphi _{1} \right )$

Os dois primeiros termos são as energias eletrostáticas de cada configuração tomadas isoladamente. Os últimos dois termos são, de facto iguais e a sua soma é a energia de interação $U_{12}$ entre as duas configurações:

$\int dV\rho _{1}\left ( \vec{r} \right )\varphi _{2}\left ( \vec{r} \right )=\int dV\rho _{1}\frac{1}{4\pi \varepsilon _{0}}\int dV'\frac{\rho _{2}\left ( \vec{r}' \right )}{\left | \vec{r}-\vec{r}' \right |}=$

$=\int dV'\rho _{2}\left ( \vec{r}' \right )\frac{1}{4\pi\varepsilon _{0}}\int dV\frac{\rho _{1}\left ( \vec{r} \right )}{\left | \vec{r}-\vec{r}' \right |}=\int dV'\rho _{1}\left ( \vec{r}' \right )\varphi _{2}\left ( \vec{r}' \right )$

Seja, então:

$U_{12}=\int dV\rho _{1}\left ( \vec{r} \right )\varphi _{2}\left ( \vec{r} \right )=\frac{1}{4\pi\varepsilon _{0}}\int dV_{1}\rho _{1}\left ( \vec{r}_{1} \right )\int dV_{2}\frac{\rho _{2}\left ( \vec{r}_{2} \right )}{\left | \vec{r}_{1}-\vec{r}_{2} \right |}$ (27)

Esta expressão é geral. Interessa agora imaginar que as duas configurações estão muito afastadas de modo a poder utilizar-se a expansão multipolar para o potencial. Para isso, escolhe-se um ponto $\left ( P_{1} \right )$ no interior da primeira distribuição e um segundo ponto $\left ( P_{2} \right )$ no interior da segunda distribuição. Seja $\vec{R}=\overrightarrow{P_{1}P_{2}}$ o vector com origem no primeiro ponto e extremidade no segundo ponto. Tome-se a origem do referencial cartesiano coincidente com P1. Se se designar por $\vec{r}_{2}$ a posição da carga elementar $dV_{2}\rho _{2}\left ( \vec{r}_{2} \right )$ em relação ao segundo ponto, então a distância entre as cargas elementares na eq. (27) é $\left | \vec{R}+\vec{r}_{2}-\vec{r}_{1} \right |$, com $\left | \vec{r}_{1} \right |,\left | \vec{r}_{2} \right |\ll \left | \vec{R} \right |\equiv R$. Então, até à primeira ordem, tem-se:

$\frac{1}{\left | \vec{R}+\vec{r}_{2}-\vec{r}_{1} \right |}=\frac{1}{R}\left [ 1+\frac{\left ( \vec{r}_{1}-\vec{r}_{2} \right )\cdot \vec{R}}{R^{2}}+\frac{3}{2}\left ( \frac{\vec{r}_{1}-\vec{r}_{2}\cdot \vec{R}}{R^{2}} \right )^{2} -\frac{1}{2}\frac{\left ( \vec{r}_{1}-\vec{r}_{2} \right )^{2}}{R^{2}}+... \right ]=$

$=\frac{1}{R}\left [ 1+\frac{\left ( \vec{r}_{1}-\vec{r}_{2} \right )\cdot \vec{R}}{R^{2}}+\frac{\vec{r}_{1}\cdot\vec{r}_{2}}{R^{2}}-3\frac{\left ( \vec{r}_{1}\cdot \vec{R} \right )\left ( \vec{r}_{2}\cdot \vec{R} \right )}{R^{4}}+... \right ]$

Substituindo na eq. (27) e integrando sobre as cargas, obtem-se (ver eq. (13) para a definição do momento dipolar):

$U_{12}=\frac{1}{4\pi\varepsilon _{0}}\left [ \frac{Q_{1}Q_{2}}{R}+\frac{Q_{2}\vec{R}\cdot \vec{p}_{1}-Q_{1}\vec{R}\cdot \vec{p}_{2}}{R^{3}}+\frac{\vec{p}_{1}\cdot \vec{p}_{2}}{R^{3}}-3\frac{\left ( \vec{p}_{1}\cdot \vec{R} \right )\left ( \vec{p}_{2}\cdot \vec{R} \right )}{R^{5}}+... \right ]$

Note-se que $U_{12}=\frac{1}{4\pi \varepsilon _{0}}\frac{Q_{1}\vec{R}}{R^{3}}\equiv \vec{E}_{1}$ é o campo elétrico gerado pela primeira distribuição no ponto $P_{2}$; do mesmo modo, $\frac{1}{4\pi\varepsilon _{0}}\frac{Q_{1}\left ( -\vec{R} \right )}{R^{3}}\equiv \vec{E}_{2}$ é o campo elétrico gerado pela segunda distribuição no ponto $P_{1}$. Em ambos os casos, a grandes distâncias das respetivas fontes. Deste modo, reescreve-se a equação anterior sob a forma:

$U_{12}=\frac{1}{4\pi\varepsilon _{0}}\frac{Q_{1}Q_{2}}{R}-\vec{E}_{1}\cdot \vec{p}_{2}-\vec{E}_{2}\cdot \vec{p}_{1}+\frac{1}{4\pi\varepsilon _{0}}\left [ \frac{\vec{p}_{1}\cdot \vec{p}_{2}}{R^{3}}-3\frac{\left ( \vec{p}_{1}\cdot \vec{R} \right )\left ( \vec{p}_{2}\cdot \vec{R} \right )}{R^{5}} \right ]$ (28)

No segundo membro, o primeiro termo é a interação Coulombiana pura como se as distribuições se reduzissem às suas cargas totais localizadas nos pontos escolhidos; os segundo e terceiro termos representam a interação do momento dipolar de uma distribuição com o campo gerado pela outra distribuição; e os últimos dois termos exibem a interação entre os momentos dipolares:

$U_{pp}\equiv \frac{1}{4\pi \varepsilon _{0}}\left [ \frac{\vec{p}_{1}\cdot \vec{p}_{2}}{R^{3}} -3\frac{\left ( \vec{p}_{1}\cdot \vec{R} \right )\left ( \vec{p}_{2}\cdot\vec{R} \right )}{R^{5}}\right ]$ (29)

Este será o termo dominante na interação entre as duas distribuições de carga se cada uma apresentar carga total nula. Note-se que a interação dipolar é fortemente anisotrópica. Ela é mínima (mais negativa) se os dipólos se alinharem paralelamente entre si e com o eixo que as une; é máxima (mais positiva) quando se alinharem antiparalelamente entre si, tendo a mesma direção daquele eixo; e é nula quando os dipólos forem perpendiculares entre si, estando um deles alinhado com o eixo.

Força e momento sobre um dipólo

Considere-se um dipólo num ponto $\vec{r}$ submetido à ação de um campo elétrico $\vec{E}\left ( \vec{r} \right )$ gerado por outra distribuição de carga – muitas vezes designado por campo aplicado. A energia de interação do dipólo com o campo é, como se viu atrás:

$U_{int}=-\vec{p}\cdot \vec{E}\left ( \vec{r} \right )$ (30)

Este resultado já havia sido obtido noutro artigo^[6]. Invocando a eq. (19), é possível agora deduzir a força e o momento que atuam sobre um dipólo. Para isso, aplicam-se os resultados deduzidos para deslocamentos ou rotações virtuais^[7]. Imagine-se que o dipólo é transportado paralelamente a si próprio da posição inicial $\vec{r}$ para a posição final em $\vec{r}+\delta \vec{r}$. Tem-se:

$\delta W=\vec{F}\cdot\delta \vec{r}=-dU_{int}=\vec{p}\cdot\left [ \vec{E}\left ( \vec{r}+\delta \vec{r} \right )-\vec{E}\left ( \vec{r} \right ) \right ]=\vec{p}\cdot \left ( \delta \vec{r}\cdot \bigtriangledown \right )\vec{E}\left ( \vec{r} \right )$

Por exemplo, $F_{x}=\vec{p}\cdot \frac{\partial \vec{E}}{\partial x}$. Quer dizer, a força é nula para um campo uniforme e, no caso de ser não uniforme, a força tem a direção do crescimento do campo. Uma experiência simples exibe este resultado. Abra-se uma torneira de água até escorrer um pequeno fio de água (FIGURA 9). Esfregando em um pano de flanela um pente de plástico e aproximando- a, sem tocar, do fio de água, ver-se-á este a encurvar em direção ao pente. Porquê? O pente ficou eletrizado pela flanela, originando um campo não uniforme que atua sobre as moléculas da água (dipólos como se viu), puxando-as para as regiões onde o campo é mais intenso.

O cálculo do momento que se exerce sobre o dipólo efetua-se começando por imaginar uma rotação infinitesimal do dipólo: $\vec{p}\rightarrow \vec{p}+\delta \vec{\Omega }\wedge \vec{p}$. Aqui, $\delta \vec{\Omega }$ define a rotação: a sua direção é o eixo de rotação, o seu sentido determina o sentido da rotação (regra do saca-rolhas) e o ângulo de rotação é $\left | \delta \vec{\Omega } \right |$. Designando por $\vec{M}$ o momento devido ao campo, tem-se:

$\delta W=\vec{M}\cdot \delta \vec{\Omega }=-dU_{int}=\delta \vec{p}\cdot \vec{E}=\delta \vec{\Omega }\wedge \vec{p}\cdot \vec{E}=\delta \vec{\Omega }\cdot \vec{p}\wedge \vec{E}$

Então, o momento que atua sobre o dipólo é:

$\vec{M}=\vec{p}\wedge \vec{E}$ (31)

Voltando à experiência do fio de água, percebe-se ainda melhor o seu resultado: as moléculas da água rodam alinhando os seus dipólos com o campo local e assim maximizam a força que o campo não uniforme sobre elas atua.

Apêndice

O potencial para uma carga pontual, eq. (3), deve ser solução da equação de Poisson, eq. (8), colocando-se a questão de qual a correspondente densidade de carga. Designe-se esta densidade por:

$\rho \left ( \vec{r} \right )=q_{1}\delta \left ( \vec{r}-\vec{r}_{1} \right )$ (32)

Aqui, $\vec{r}_{1}$ é a posição da carga e a “função” $\delta \left ( \vec{r}-\vec{r}_{1} \right )$ deve satisfazer a seguinte condição óbvia que decorre da definição de densidade de carga:

$\int_{D}^{}dV\delta \left ( \vec{r}-\vec{r}_{1} \right )=\left\{\begin{matrix} 1\; \; \; \leftrightarrow \; \; \; \vec{r}_{1}\; \textrm{no interior de D}\\ 0\; \; \; \leftrightarrow \; \; \; \vec{r}_{1}\; \textrm{no exterior de D} \end{matrix}\right.$ (33)

Assim, inserindo a eq. (3) na equação de Poisson, obtém-se uma muito útil solução particular, que se reescreve sob a forma:

$\Delta\left ( \frac{1}{\left | \vec{r}-\vec{r}_{1} \right |} \right )=-4\pi\delta \left ( \vec{r}-\vec{r}_{1} \right )$ (34)

Note-se que o laplaciano actua sobre as coordenadas de $\vec{r}$.

A “função” $\delta \left ( \vec{r}-\vec{r}_{1} \right )$ é, na verdade, o produto de três distribuições de Dirac:

$\delta \left ( \vec{r}-\vec{r}_{1} \right )=\delta \left ( x-x_{1} \right )\delta \left ( y-y_{1} \right )\delta \left ( z-z_{1} \right )$

Para cada uma delas, é verdadeira a seguinte propriedade:

$\int_{a}^{b}dx\delta \left ( x-x_{1} \right )=1\; \; \; \leftrightarrow \; \; \; x_{1}\in \left ] a,b \right [$

O integral é nulo se $x_{1}$ se situar fora do intervalo de integração. A distribuição de Dirac é a generalização, para funções contínuas, do símbolo de Kronecker^[8].

[editar] Referências

1. ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
2. ↑ LAGE, E., Gradiente, divergência e rotacional, Rev. Ciência Elem., V8(2):029. (2020). DOI: 10.24927/rce2020.029.
3. ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
4. ↑ LAGE, E., Escalares, vetores e tensores cartesianos, Rev. Ciência Elem., V6(4):086. (2018). DOI: 10.24927/rce2018.086.
5. ↑ LAGE, E., Os fundamentos do eletromagnetismo, Rev. Ciência Elem., V9(1):016. (2021). DOI: 10.24927/rce2021.016.
6. ↑ LAGE, E., Trabalho do campo eletromagnético em dielétricos e magnetes, Rev. Ciência Elem., V7(4):077. (2019). DOI: 10.24927/rce2019.077.
7. ↑ LAGE, E. O sólido rígido, Rev. Ciência Elem., V8(3):044. (2020). DOI: 10.24927/rce2020.044.
8. ↑ LAGE, E., Escalares, vetores e tensores cartesianos, Rev. Ciência Elem., V6(4):086. (2018). DOI: 10.24927/rce2018.086.

---

Criada em 27 de Julho de 2020
Revista em 12 de Fevereiro de 2021
Aceite pelo editor em 15 de Março de 2021