Derivada
Referência : Tavares, J. N., (2018) Derivada, Rev. Ciência Elem., V6(1):089
Autor: João Nuno Tavares
Editor: José Ferreira Gomes
DOI: [https://doi.org/10.24927/rce2018.089]

Dada uma função 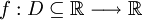 define-se a taxa média de variação de f num ponto a,
interior ao domínio de f, através de
define-se a taxa média de variação de f num ponto a,
interior ao domínio de f, através de
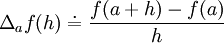
(depende de a, h e, é claro, de f). A definição faz sentido uma vez que se a é ponto interior ao domínio D de f, a pertence a um intervalo aberto contido em D. Portanto,
se 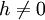 é suficientemente pequeno,
é suficientemente pequeno, 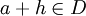 .
.
A derivada de f no ponto a é a taxa instantânea de variação de f no ponto a, isto é
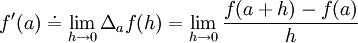
quando este limite existe. A derivada de f no ponto a, depende apenas do comportamento local de f numa vizinhança de a - é pois um conceito local.
Pondo 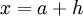 , o que implica que
, o que implica que 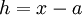 , e substituindo na definição anterior, podemos dar uma outra forma à definição de derivada de f no ponto a
, e substituindo na definição anterior, podemos dar uma outra forma à definição de derivada de f no ponto a
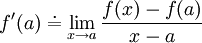
uma vez que 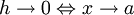 .
.
Criada em 25 de Novembro de 2009
Revista em 19 de Abril de 2012
Aceite pelo editor em 31 de Março de 2018

