Crescimento da população
Referência : Nápoles, S., (2018) O crescimento exponencial de populações: Euler ou Malthus?, Rev. Ciência Elem., V6(2):041
Autor: Suzana Nápoles
Editor: José Ferreira Gomes
DOI: [http://doi.org/10.24927/rce2018.041]

Em 1798, no livro An Essay on the Principle of Population, que teve seis edições, Thomas Malthus (1766-1864), um clérigo e erudito inglês influente nos campos da economia política e da demografia, escreveu:
“A população, quando não controlada, aumenta em progressão geométrica. A subsistência aumenta apenas em progressão aritmética. Um pequeno conhecimento dos números mostrará a imensidão do primeiro poder em comparação com o segundo.“
Malthus não tentou traduzir matematicamente o seu modelo de crescimento. Limitou-se a caraterizá-lo pressupondo que a taxa segundo a qual a população cresce num determinado instante é proporcional à população total nesse mesmo instante.
Numa revisão da primeira edição discutiu em detalhe os obstáculos para o crescimento da população em vários países, nomeadamente atraso no casamento, aborto, infanticídio, fome, guerra, epidemias e fatores económicos. Para ele, o casamento retardado era a melhor opção para estabilizar a população.
Para caraterizar matematicamente este modelo, considerando o crescimento em anos consecutivos e supondo uma taxa de crescimento r em cada ano, se num ano n a população é \(P_n\) no ano seguinte a população será \(P_{n+1}=(1+r)P_n\), pelo que \(P_{n+1}=(1+r)^nP_0\) e o crescimento é descrito por uma progressão geométrica de razão \(1+r\).

Supondo uma variação contínua do tempo, e designando por \(P(t)\) a população no instante t e por r a taxa de crescimento por unidade de tempo, a equação diferencial que traduz o modelo contínuo preconizado por Malthus é \(P'(t)=rP(t)\). Então, \(P(t)=ke^{rt}\) com k constante.
Como \(P(0)=k\), e \(P_0\) o número de indivíduos no ano zero, a evolução da população é dada por \(P(t) = P_0 e^{rt}\).
Acontece que 50 anos antes, em Introductio in analysin infinitorum, no VI capítulo “De quantidades exponenciais e logaritmos” para ilustrar a grande utilidade das tabelas de logaritmos para abreviar cálculos numéricos, o matemático suíço Leonhard Euler (1707-1783) dá vários exemplos que envolvem o crescimento populacional, de que transcrevemos os exemplos II e III.

|

|
FIGURA 2. Leonhard Euler e o seu Introductio in analysin infinitorum.
Exemplo II
“Se a população em certa região aumenta anualmente um trigésimo e, por outro lado, lá habitavam no princípio 100000 pessoas, pergunta-se qual o número de habitantes após 100 anos.
Seja o número inicial = n, pelo que n = 100000; passado um ano o número de habitantes será \(=(1+\frac{1}{30})n=\frac{31}{30}n\): depois de dois anos = \(\left(\begin{array}{c}\frac{31}{30}\end{array}\right)^2n\); ao cabo de três, \(\left(\begin{array}{c}\frac{31}{30}\end{array}\right)^3n\), e daqui depois de 100 anos será \(=\left(\begin{array}{c}\frac{31}{30}\end{array}\right)^{100}n=\left(\begin{array}{c}\frac{31}{30}\end{array}\right)^{100} 100000\): cujo logaritmo é \(= 100 l \frac{31}{30}+l100000\). E \(l \frac{31}{30}=l31-l10= 0,014240439\) de onde, \(100 l \frac{31}{30}=1,4240439\), que somando-lhe \(l 100000 = 5\) será o logaritmo do número de habitantes procurado, \(= 6,4240439\), a que corresponde o número 2654874.
Assim ao cabo de 100 anos será mais de vinte e seis vezes maior.”
Este exemplo publicado em 1748 é, meio século antes, a concretização do “Modelo Malthusiano” para uma população de 100000 habitantes e uma taxa de crescimento anual de 1/30.
No exemplo seguinte Euler faz alusão ao capítulo 7 do Livro do Genesis que relata como um dilúvio reduziu a população da terra a seis seres humanos.
Exemplo III
“Como a humanidade se espalhou após o dilúvio por obra de seis seres humanos, se o número destes alcançar duzentos anos depois o número 1000000, pergunta-se em que parte deveria crescer anualmente o número de humanos.
Se aumentar em cada ano \(\frac{1}{x}\), duzentos anos depois o número de humanos seria \(=\left(\begin{array}{c}\frac{1+x}{x}\end{array}\right)^{200} 6 = 1000000\) e por tanto \(\frac{1+x}{x}=\left(\begin{array}{c}\frac{1000000}{6}\end{array}\right)^{\frac{1}{200}}\).
Portanto \(l\frac{1+x}{x}=\frac{1}{200}l\frac{1000000}{6}=\frac{1}{200}. 5,2218487 = 0,0261092\)
e assim \(\frac{1+x}{x}=\frac{1061963}{1000000}\) e 1000000 = 61963x donde x =16 aproxidamente.
Bastará pois que os humanos aumentem por ano a sua décima sexta parte [...]. Contudo, se o número de homens tivesse crescido na mesma proporção durante um intervalo de 400 anos, deveria chegar a 1000000. \(\frac{1000000}{6}= 166666666666\), cujo sustento a terra inteira não seria de forma alguma capaz de dar.”
Euler, ao abordar o crescimento das populações, tinha uma preocupação matemática – a de mostrar a utilidade dos logaritmos – que ilustrou com exemplos.
Mas a observação anterior leva a crer que ele considerou o modelo exponencial desadequado para o estudo do crescimento populacional.
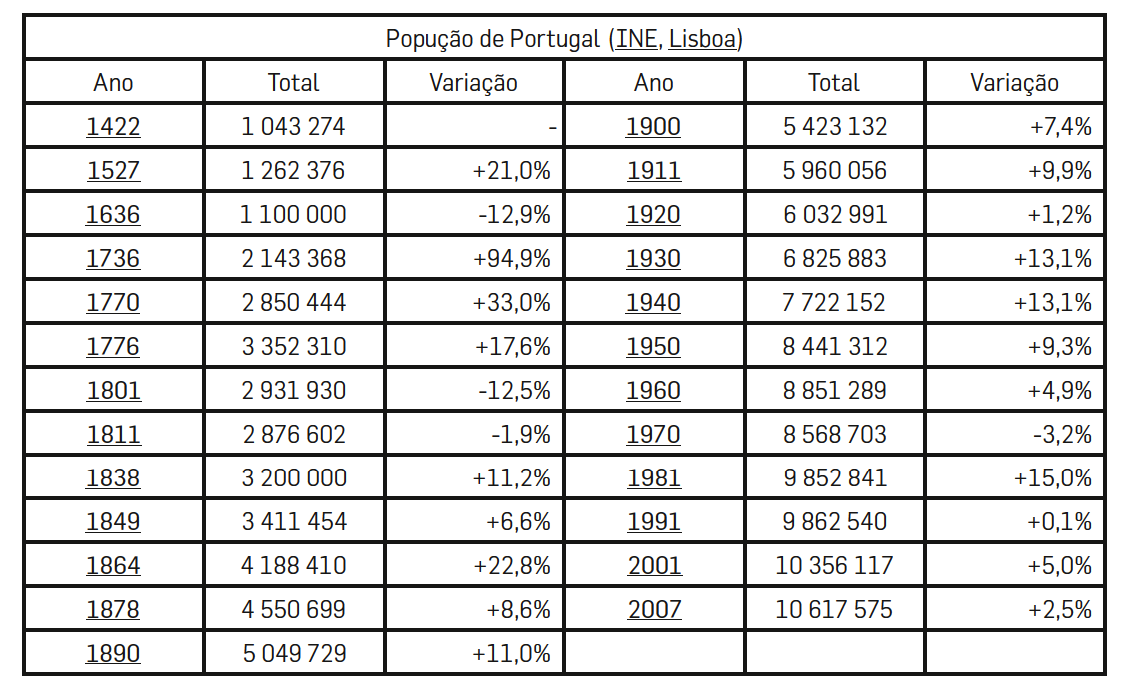
A população de Portugal espelha bem a falência deste modelo. Segundo dados do Instituto Nacional de Estatística, nos duzentos anos que decorreram entre 1770 e 1970, a população nem chegou a triplicar.
TABELA 1. População de Portugal entre 1422 a 1890.
Quanto a Malthus, as suas preocupações eram de natureza política e legislativa. Tomou como certo um crescimento exponencial da população mundial que conduziria a uma catástrofe por ausência de recursos e, para o travar, sugeriu o recurso a políticas adequadas. Ao publicitar o modelo exponencial - que ficou conhecido como Modelo Malthusiano - ligando-o a problemas legislativos reais, abriu caminho para que diferentes matemáticos se dedicassem à modelação do crescimento populacional.
Em 1844, o matemático belga Pierre Verhulst (1804-1849) propôs no artigo Recherches mathématiques sur la loi d’accroissement de la population, um modelo em que considera que, à medida que a população se aproxima de um valor máximo, a taxa de crescimento diminui: “O aumento virtual da população é, portanto, limitado pelo tamanho e pela fertilidade do país. Como resultado, a população fica cada vez mais próxima de um estado estável”.
Designado por P(t) a população no instante t, por r a taxa de crescimento por unidade de tempo e por M o número máximo de indivíduos que a região pode suportar, este modelo exprime-se pela equação diferencial
\(\frac{dP}{dt}=rP\left(\begin{array}{c}1-\frac{P(t)}{M}\end{array}\right)\),
cuja solução é
\(P(t)= \frac{P(0)e^{rt}}{1+\frac{P(0)(e^{rt}-1)}{M}}\),
Se P(t) for muito pequeno face a M tem-se que \(\frac{dP}{dt}≅ r P(t)\) que tem a solução \(P(t) ≅ P(0) e^{rt}\), e o crescimento é exponencial.

|
|
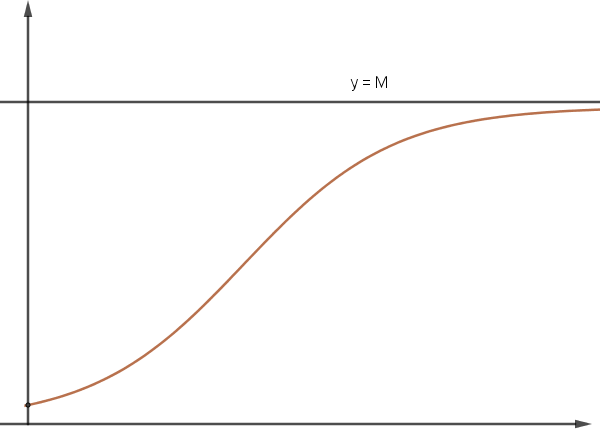
FIGURA 4. Pierre François Verhulst e o gráfico da curva logística.
À medida que t cresce a população aproxima-se assintoticamente de M. A equação diferencial que carateriza este modelo é atualmente designada por equação logística e a população máxima M por capacidade de carga. Com Verhulst relativizou-se “a hipótese da progressão geométrica, uma vez que ela só se pode verificar em circunstâncias muito especiais; por exemplo, quando um território fértil de tamanho quase ilimitado passa a ser habitado por pessoas com uma civilização avançada, como foi o caso das primeiras colónias americanas”.
Essa equação foi retomada por vários matemáticos e adaptada a contextos variados. São de realçar os casos em que a capacidade de carga varia como o tempo conduzindo ao modelo caraterizado pela equação diferencial
\(\frac{dP}{dt}=rP\left(\begin{array}{c}1-\frac{P}{M(t)}\end{array}\right)\)
onde a capacidade de carga M(t) = M(t +T) varia periodicamente com período T.
|

|
FIGURA 5. A demografia é instrumental para o controlo das populações humanas.
Desde o século XVIII que o estudo da dinâmica das populações é objeto de modelação matemática. Na atualidade existem outros modelos de crescimento: hiperbólicos, exponenciais, logísticos ou baseados noutras funções. Baseada nos modelos populacionais do matemático Song Jian, a República Popular da China em 1980, então a atingir o bilião de habitantes, instaurou uma política estrita de filho único. Essa lei foi flexibilizada em 2015, aumentando para dois o número máximo de filhos, para fazer frente ao envelhecimento da população e à redução do grupo de trabalhadores na faixa etária considerada economicamente ativa.
Muitos dos pareceres científicos nas mais diversas áreas baseiam-se em modelos matemáticos que podem permitir fazer estimativas e previsões, mas … ao olhar para o crescimento populacional ao longo dos tempos verificamos que os modelos matemáticos são instrumentais na análise da dinâmica das populações.
[editar] Referências
- BACAËR, N., A Short History of Mathematical Population Dynamics, Springer-Verlag, London, 2011.
- EULER, L., Introductio in analysin infinitorum, translated and annotated by Ian Bruce, 2013.
- KOROTAYEV, A., et al, Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth, 2006.
- MALTHUS, T., An Essay on the Principle of Population, London, 1798.
- VERHULTS, P. F., Recherches mathématiques sur la loi d’accroissement de la population. NouveauxMémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles, 18, 14-54, 1845.
Criada em 3 de Maio de 2018
Revista em 27 de Maio de 2018
Aceite pelo editor em 18 de Junho de 2018

