Constante de Avogadro
Referência : Fernandes, R.F., (2015) Constante de Avogadro, Rev. Ciência Elem., V3(3):191
Autor: Ricardo Ferreira Fernandes
Editor: Jorge Gonçalves
DOI: [http://doi.org/10.24927/rce2015.191]
A constante de Avogadro é uma constante física fundamental, representada pelo símbolo NA (ou L), que corresponde ao número de entidades elementares (átomos, moléculas, iões, radicais, electrões, fotões, etc.) existentes numa mole da substância considerada. Esta constante tem o valor de 6,022 141 79 (30) x 1023, correspondente ao número de átomos existentes em exactamente 0,012 kg de carbono-12† e apresenta as dimensões de mol-1.
A constante de Avogadro foi introduzida, em 1909, pelo físico francês Jean Perrin em homenagem ao químico e físico italiano Amedeo Avogadro (figura 1) que, em 1811, publicou que: volumes iguais de gases nas mesmas condições de temperatura e pressão contêm o mesmo número de moléculas.[1]
No início do século XX utilizava-se o termo molécula-grama para designar a massa de uma determinada substância que no estado gasoso ocupava o mesmo volume que dois gramas de hidrogénio (em iguais condições de pressão e temperatura). Assim, com base no conceito de molécula-grama, Perrin propôs que a afirmação de Avogadro era equivalente a dizer que quaisquer duas moléculas-grama contêm sempre o mesmo numero N de moléculas, logo, N é uma constante universal invariável, à qual seria apropriado que se designasse por constante de Avogadro.[2]
Jean Perrin, que foi laureado com o prémio Nobel da Física em 1926, calculou a constante de Avogadro a partir do movimento browniano de partículas coloidais. Porém, não foi o primeiro cientista a determinar o seu valor. Em 1865, o cientista austríaco Johann Josef Loschmidt com base na teoria cinética dos gases determinou a densidade numérica de partículas existentes num determinado volume de gás, actualmente conhecida como constante de Loschmidt. É por causa de Loschmidt que, por vezes, se utiliza o símbolo L para representar a constante de Avogadro.
Desde as primeiras estimativas até à actualidade, diferentes métodos foram utilizados para determinar a constante de Avogadro. Esta constante pode ser determinada a partir da teoria cinética dos gases, a partir do movimento browniano, por métodos electroquímicos, a partir da teoria do corpo negro da radiação, pela contagem das partículas alfa resultantes de decaimento radioactivo ou a partir densidade cristalina obtida por raio-X. Em 1965, o valor da constante de Avogadro foi obtido com grande precisão através da utilização da interferometria de raio-X em conjunto com o uso de um cristal perfeito de silício (Si). Note-se que os valores da constante de Avogadro determinados pelas diferentes técnicas são concordantes entre si, o que confirma o postulado da existência da átomos e moléculas proposto há cerca de dois séculos.[3,4]
Como já foi referido, a constante de Avogadro, quando foi proposta por Perrin, referia-se à quantidade de entidades elementares existentes numa molécula-grama - unidade daquela época para especificar a quantidade de um composto ou de um elemento químico. No entanto, em 1971, na 14ª Conferência de Pesos e Medidas introduziu-se quantidade de substância como grandeza fundamental do Sistema Internacional, tendo-se adoptado a mole como unidade (representada pelo símbolo mol). Assim, por proposta da IUPAC, da IUPAP e da ISO, a mole foi definida como a quantidade de substância de um sistema que contém tantas entidades elementares como o número de átomos existentes em 0,012 kg de carbono-12; em que a natureza das entidades elementares (átomos, moléculas, electrões, protões, etc.) tem de ser especificada.[5] A introdução da mole como unidade de quantidade de substância conduziu a que a constante de Avogadro passasse a ser formalmente definida como o número de átomos existentes em exactamente 0,012 kg de Carbono-12.
O número de entidades elementares existentes numa pequena porção de substância é de tal modo elevado, que seria um processo praticamente infinito determinar o número de entidades elementares aí existentes. Assim, a constante de Avogadro permite fazer a transição entre o microscópico e o macroscópico, isto é, conhecendo a massa de uma substância e a massa molar, é possível a partir da constante de Avogadro determinar o número N de entidades elementares aí existentes.
Considere-se, como exemplo, 30,35642 g de sódio. O sódio tem uma massa molar, M, igual a 22,98976928 g∙mol-1. Logo, o quociente entre a massa de sódio, m, e a respectiva massa molar, M, é a quantidade (em moles) de sódio nessa amostra. Essa quantidade multiplicada pela constante de Avogadro permite determinar o número de átomos existentes:
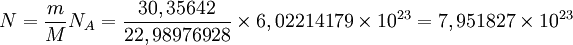átomos de sódio (Na)
Verifica-se assim que 30,35642 g de sódio contêm 7.951827 x 1023 átomos.
Para entender melhor a magnitude do número 6,022
1023 (valor numérico da constante de Avogadro), imagine-se que se tinha como desafio contar o número de partículas existentes numa mole durante o intervalo de tempo correspondente à idade estimada do planeta terra, ou seja, cerca de 4,5 mil milhões de anos (4,5 x 109 anos). Logo, para superar o desafio era necessário contar 4,2 milhões de partículas por segundo durante os 4,5 mil milhões de anos!
†Os átomos de carbono-12 devem estar no seu estado fundamental e não estarem quimicamente ligados entre si.
Referências
1. Essay on a Manner of Determining the Relative Masses of the Elementary Molecules of Bodies, and the Proportions in Which They Enter into These Compounds, consultado em 12/06/2010.
2. Brownian Motion and Molecular Reality, consultado em 12/06/2010.
3. S. Ramaseasha, Resonance 11 (2006) 79-87, DOI:10.1007/BF02835688.
4. P. Becker, H. Friedrich, K. Fujii,W. Giardini, G. Mana, A. Picard. H. Pohl, H. Riemann, S. Valkiers, Meas. Sci. Technol. 20 (2009) DOI: 10.1088/0957-0233/20/9/092002, consultado em 12/06/2010).
5. International Bureau of Weights and Measures, 8th ed. (2006) 114–115, consultado em 12/06/2010.
Criada em 10 de Dezembro de 2010
Revista em 01 de Fevereiro de 2011
Aceite pelo editor em 02 de Fevereiro de 2011
